18.2.1.2 矩形的判定 课件(共20张PPT)
文档属性
| 名称 | 18.2.1.2 矩形的判定 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1018.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 17:49:17 | ||
图片预览






文档简介
(共20张PPT)
18.2.1.2 矩形的判定
1.理解并掌握矩形的判定办法.
2.能熟练运用矩形的定义和判定知识进行计算和证明.
1.矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
2.矩形有哪些性质?
矩形的四个角都是直角.
矩形的对角线相等.
矩形是轴对称图形.
如何判定一个四边形是矩形呢?
类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
除定义外,还有没有其他的方法能判定是矩形呢?
我们能根据矩形的性质得到矩形的判定方法吗?
接下来我们研究矩形性质的逆命题是否成立.
问题1 我们已经研究了矩形的四个角,知道它们都是直角,它的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
成立
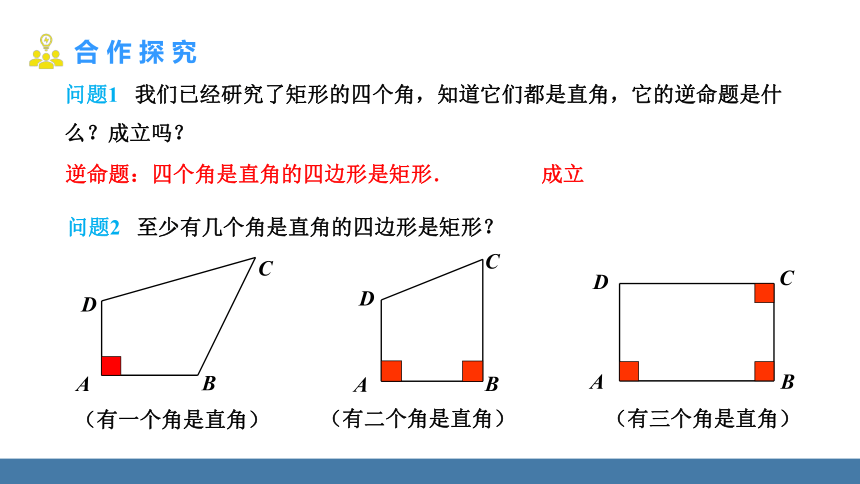
问题2 至少有几个角是直角的四边形是矩形?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
A
B
C
D
猜想:有三个角是直角的四边形是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
矩形的判定定理1
有三个角是直角的四边形是矩形.
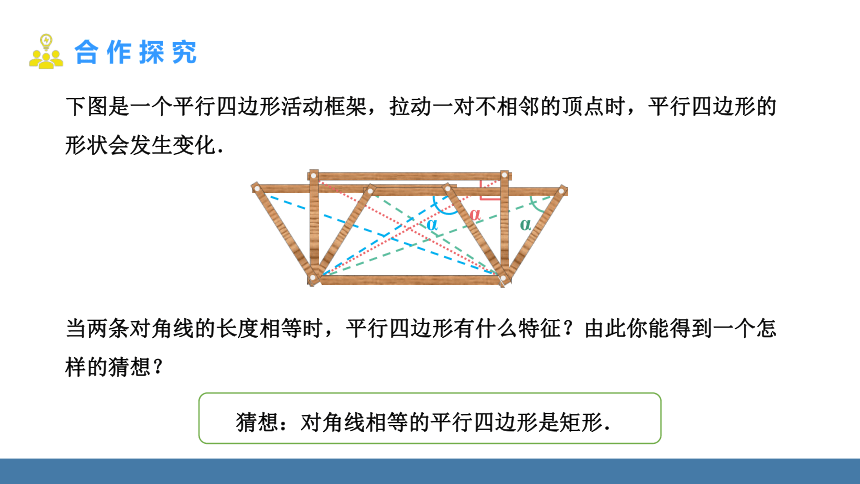
下图是一个平行四边形活动框架,拉动一对不相邻的顶点时,平行四边形的形状会发生变化.
α
α
α
当两条对角线的长度相等时,平行四边形有什么特征?由此你能得到一个怎样的猜想?
猜想:对角线相等的平行四边形是矩形.
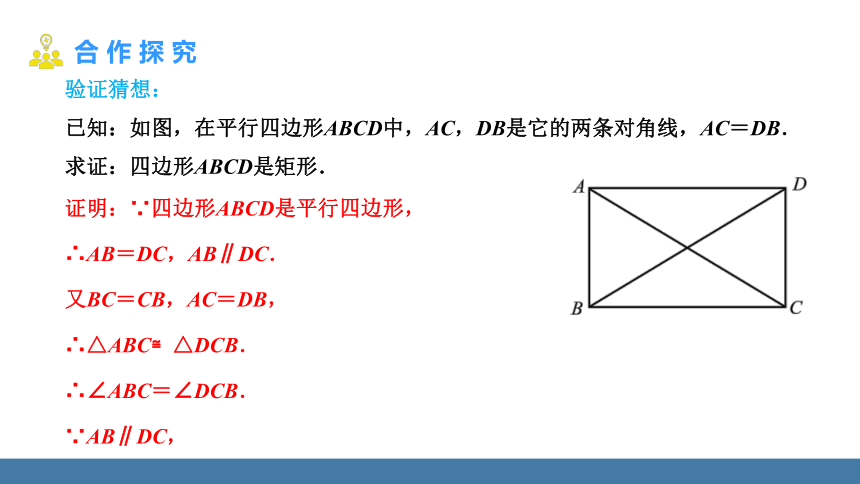
验证猜想:
已知:如图,在平行四边形ABCD中,AC,DB是它的两条对角线,AC=DB.
求证:四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC.
又BC=CB,AC=DB,
∴△ABC≌△DCB.
∴∠ABC=∠DCB.
∵AB∥DC,
矩形的判定定理2 对角线相等的平行四边形是矩形.
∴∠ABC+∠DCB=180°.
∴∠ABC=∠DCB=×180°=90°.
∴四边形ABCD是矩形.
例1 如图,在平行四边形 ABCD 中,对角线 AC,BD 相交于点O,且 OA=OD,∠OAD=50°. 求 ∠OAB 的度数.
解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD.
A
D
B
C
O
又∠OAD=50°,∴ ∠OAB=40°.
又OA=OD,∴ AC=BD,
∴四边形ABCD是矩形, ∴∠DAB=90 .
例2 已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.
证明:∵AD平分∠BAC,AN平分∠CAM,
∴∠CAD=∠BAC,∠CAN=∠CAM.
∴∠DAE=∠CAD+∠CAN
=(∠BAC+∠CAM)
=×180°=90°.
例2 已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.
在△ABC中,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC.∴∠ADC=90°.
又CE⊥AN,
∴∠CEA=90°.
∴四边形ADCE是矩形.
在例2中,连接DE,交AC于点F.
(1)试判断四边形ABDE的形状,并证明你的结论.
F
四边形ABDE是平行四边形.
证明:∵四边形ADCE为矩形,
∴AE∥DC,AE=DC.
在△ABC中,∵AB=AC,AD为∠BAC的平分线,
∴BD=DC.
∴AE∥BD,AE=BD.
∴四边形ABDE为平行四边形.
证明:∵四边形ADCE为矩形,
∴DF=EF=DE,
又四边形ABDE为平行四边形,
∴AB∥DE,AB=DE,
∴DF∥AB,DF=AB.
DF∥AB,DF=AB.
F
在例2中,连接DE,交AC于点F.
(2)线段DF与AB有怎样的关系?请证明你的结论.
1.判断下列语句的对错.
(1)有一个角是直角的四边形是矩形. ( )
(2)四个角都相等的四边形是矩形. ( )
(3)对角线相等的四边形是矩形. ( )
(4)对角线相等且互相平分的四边形是矩形. ( )
×
√
×
√
平行四边形
平行四边形
2. 已知平行四边形ABCD,下列条件中,不能判定这个平行四边形是矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
B
解析:对于A, ∵ ∠A=∠B, ∠A+∠B=180°,∴∠A=∠B=90°,
∴平行四边形ABCD是矩形.
对于C ,∵AC=BD,∴平行四边形ABCD是矩形.
对于D, ∵AB⊥BC , ∴∠B=90 ,
∴平行四边形ABCD是矩形.
3.在平行四边形ABCD中,对角线AC,BD相交于点O,△ABO是等边三角形.
求证:平行四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴ OA=OC=AC,OB=OD=BD.
∵ △ABO是等边三角形,
∴ OA=OB,∴ AC=BD,
∴ 平行四边形ABCD是矩形.
A
B
D
C
O
4.如图,平行四边形ABCD四个内角的平分线围成四边形EFGH,猜想四边形EFGH的形状,并说明理由.
A
B
D
C
H
E
F
G
理由:∵四边形ABCD是平行四边形,
∴∠DAB+∠ABC=180°.
同理,∠EFG=90°,∠FGH=90°.
∴四边形EFGH是矩形.
∵AE,BE分别平分∠DAB,∠ABC, ∴∠EAB+∠EBA=90°.
∴∠AEB=90°,即∠HEF=90°.
解:四边形EFGH是矩形.
矩形的判定
有一个角是直角的平行四边形是矩形
有三个角是直角的四边形是矩形
对角线相等的平行四边形是矩形
18.2.1.2 矩形的判定
1.理解并掌握矩形的判定办法.
2.能熟练运用矩形的定义和判定知识进行计算和证明.
1.矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
2.矩形有哪些性质?
矩形的四个角都是直角.
矩形的对角线相等.
矩形是轴对称图形.
如何判定一个四边形是矩形呢?
类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
除定义外,还有没有其他的方法能判定是矩形呢?
我们能根据矩形的性质得到矩形的判定方法吗?
接下来我们研究矩形性质的逆命题是否成立.
问题1 我们已经研究了矩形的四个角,知道它们都是直角,它的逆命题是什么?成立吗?
逆命题:四个角是直角的四边形是矩形.
成立
问题2 至少有几个角是直角的四边形是矩形?
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
A
B
C
D
猜想:有三个角是直角的四边形是矩形.
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
矩形的判定定理1
有三个角是直角的四边形是矩形.
下图是一个平行四边形活动框架,拉动一对不相邻的顶点时,平行四边形的形状会发生变化.
α
α
α
当两条对角线的长度相等时,平行四边形有什么特征?由此你能得到一个怎样的猜想?
猜想:对角线相等的平行四边形是矩形.
验证猜想:
已知:如图,在平行四边形ABCD中,AC,DB是它的两条对角线,AC=DB.
求证:四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC.
又BC=CB,AC=DB,
∴△ABC≌△DCB.
∴∠ABC=∠DCB.
∵AB∥DC,
矩形的判定定理2 对角线相等的平行四边形是矩形.
∴∠ABC+∠DCB=180°.
∴∠ABC=∠DCB=×180°=90°.
∴四边形ABCD是矩形.
例1 如图,在平行四边形 ABCD 中,对角线 AC,BD 相交于点O,且 OA=OD,∠OAD=50°. 求 ∠OAB 的度数.
解:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD.
A
D
B
C
O
又∠OAD=50°,∴ ∠OAB=40°.
又OA=OD,∴ AC=BD,
∴四边形ABCD是矩形, ∴∠DAB=90 .
例2 已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.
证明:∵AD平分∠BAC,AN平分∠CAM,
∴∠CAD=∠BAC,∠CAN=∠CAM.
∴∠DAE=∠CAD+∠CAN
=(∠BAC+∠CAM)
=×180°=90°.
例2 已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN为△ABC的外角∠CAM的平分线,CE⊥AN,垂足为E.求证:四边形ADCE是矩形.
在△ABC中,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC.∴∠ADC=90°.
又CE⊥AN,
∴∠CEA=90°.
∴四边形ADCE是矩形.
在例2中,连接DE,交AC于点F.
(1)试判断四边形ABDE的形状,并证明你的结论.
F
四边形ABDE是平行四边形.
证明:∵四边形ADCE为矩形,
∴AE∥DC,AE=DC.
在△ABC中,∵AB=AC,AD为∠BAC的平分线,
∴BD=DC.
∴AE∥BD,AE=BD.
∴四边形ABDE为平行四边形.
证明:∵四边形ADCE为矩形,
∴DF=EF=DE,
又四边形ABDE为平行四边形,
∴AB∥DE,AB=DE,
∴DF∥AB,DF=AB.
DF∥AB,DF=AB.
F
在例2中,连接DE,交AC于点F.
(2)线段DF与AB有怎样的关系?请证明你的结论.
1.判断下列语句的对错.
(1)有一个角是直角的四边形是矩形. ( )
(2)四个角都相等的四边形是矩形. ( )
(3)对角线相等的四边形是矩形. ( )
(4)对角线相等且互相平分的四边形是矩形. ( )
×
√
×
√
平行四边形
平行四边形
2. 已知平行四边形ABCD,下列条件中,不能判定这个平行四边形是矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
B
解析:对于A, ∵ ∠A=∠B, ∠A+∠B=180°,∴∠A=∠B=90°,
∴平行四边形ABCD是矩形.
对于C ,∵AC=BD,∴平行四边形ABCD是矩形.
对于D, ∵AB⊥BC , ∴∠B=90 ,
∴平行四边形ABCD是矩形.
3.在平行四边形ABCD中,对角线AC,BD相交于点O,△ABO是等边三角形.
求证:平行四边形ABCD是矩形.
证明:∵四边形ABCD是平行四边形,
∴ OA=OC=AC,OB=OD=BD.
∵ △ABO是等边三角形,
∴ OA=OB,∴ AC=BD,
∴ 平行四边形ABCD是矩形.
A
B
D
C
O
4.如图,平行四边形ABCD四个内角的平分线围成四边形EFGH,猜想四边形EFGH的形状,并说明理由.
A
B
D
C
H
E
F
G
理由:∵四边形ABCD是平行四边形,
∴∠DAB+∠ABC=180°.
同理,∠EFG=90°,∠FGH=90°.
∴四边形EFGH是矩形.
∵AE,BE分别平分∠DAB,∠ABC, ∴∠EAB+∠EBA=90°.
∴∠AEB=90°,即∠HEF=90°.
解:四边形EFGH是矩形.
矩形的判定
有一个角是直角的平行四边形是矩形
有三个角是直角的四边形是矩形
对角线相等的平行四边形是矩形
