18.2.2.2 菱形的判定 课件(共17张PPT)
文档属性
| 名称 | 18.2.2.2 菱形的判定 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1023.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 17:50:07 | ||
图片预览



文档简介
(共17张PPT)
18.2.2.2 菱形的判定
1.掌握菱形的判定及证明过程.
2.能熟练运用菱形的判定进行计算和证明.
有一组邻边相等的平行四边形叫做菱形.
是轴对称图形,对角线所在的直线是对称轴.
四条边相等.
对角线互相垂直.
菱形的性质
对角线互相平分.
对角相等.
对边平行且相等.
菱形是如何定义的?菱形有哪些性质?
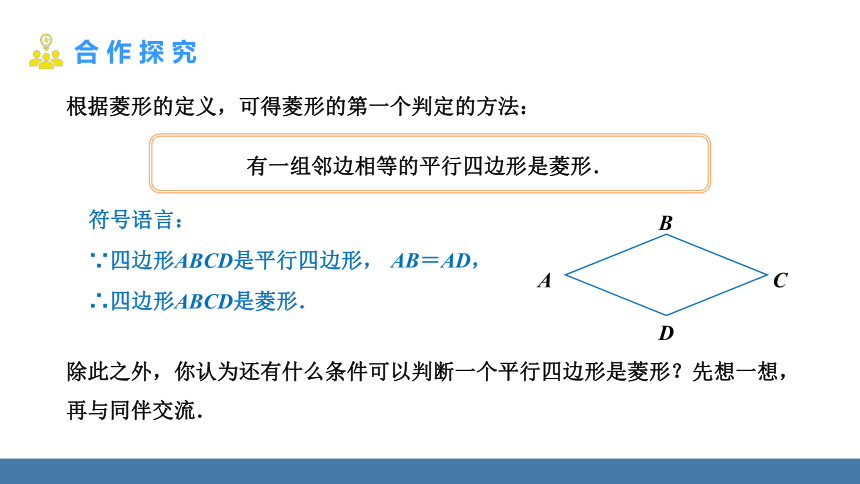
根据菱形的定义,可得菱形的第一个判定的方法:
AB=AD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
有一组邻边相等的平行四边形是菱形.
除此之外,你认为还有什么条件可以判断一个平行四边形是菱形?先想一想,再与同伴交流.
B
A
C
D
符号语言:
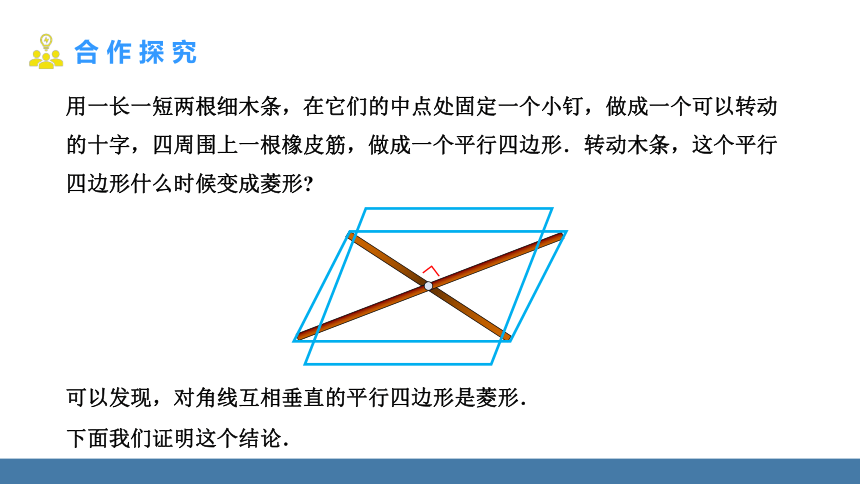
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.转动木条,这个平行四边形什么时候变成菱形
可以发现,对角线互相垂直的平行四边形是菱形.
下面我们证明这个结论.
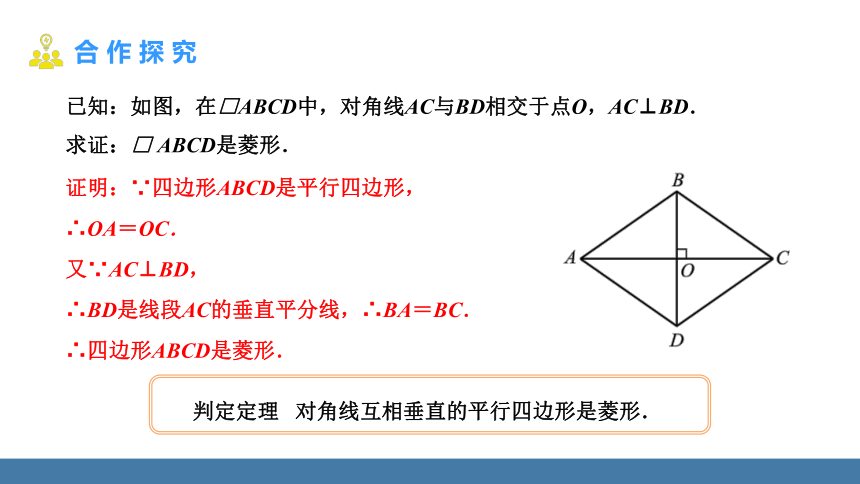
已知:如图,在□ABCD中,对角线AC与BD相交于点O,AC⊥BD.
求证:□ ABCD是菱形.
判定定理 对角线互相垂直的平行四边形是菱形.
证明:∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线,∴BA=BC.
∴四边形ABCD是菱形.
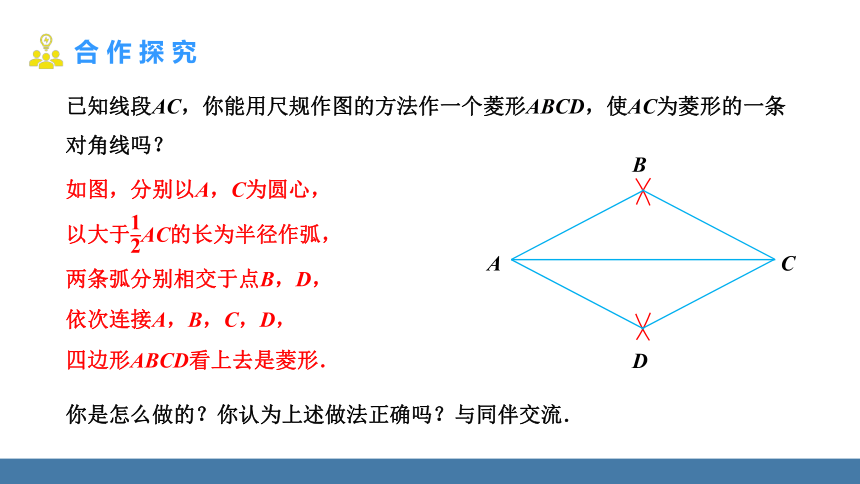
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
A
C
B
D
你是怎么做的?你认为上述做法正确吗?与同伴交流.
如图,分别以A,C为圆心,
以大于AC的长为半径作弧,
两条弧分别相交于点B,D,
依次连接A,B,C,D,
四边形ABCD看上去是菱形.
判定定理 四条边相等的四边形是菱形.
由前面的探究可以得到定理如下:
请你完成这个定理的证明.
A
B
C
D
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:∵AB=BC=CD=AD,
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又AB=BC,
∴四边形ABCD是菱形.
你能用折纸的办法得到一个菱形吗?动手试一试!
先将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,将纸展开,就得到了一个菱形.
展开
你能说说这样做的道理吗?
因为四边相等的四边形是菱形.
例1 如图,在菱形ABCD中,对角线AC, BD相交于点O,点E,F,G,H 分别是OA,OB,OC,OD的中点.
求证:四边形EFGH是菱形.
D
A
B
C
O
E
F
G
H
分析:利用三角形的中位线定理,证明四边形EFGH的四条边相等即可.
证明: ∵四边形ABCD是菱形,
∴ AB=BC=CD=AD.
∵点E,F,G,H分别是OA,OB,OC,OD的中点,
∴EF,FG,GH,EH分别是△AOB, △BOC, △COD, △AOD的中位线,
∴ EF=AB,FG=BC,GH=CD,EH=AD,
∴EF=FG=GH=EH,
∴四边形EFGH是菱形.
D
A
B
C
O
E
F
G
H
例2 如图,在□ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF. 求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,
∴ AD=BC, AD//BC.
∵ DE=BF, ∴ AE=CF.
又AE//CF, ∴四边形AECF是平行四边形.
A
B
C
D
E
F
∵ AC⊥EF,
∴四边形AECF是菱形.
1.如图所示,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,两弧相交于点C,D,则直线CD即为所求.连接AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形
C.正方形 D.等腰梯形
解析:由题意知AC=AD=BD=BC,
∴四边形ADBC一定是菱形.
B
2.如图,AD是△ABC的一条角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.求证:四边形AEDF是菱形.
证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠EDA=∠DAF.
∵AD是△ABC的一条角平分线,
∴∠EAD=∠DAF.
∴∠EDA=∠EAD,
∴EA=ED.
∴四边形AEDF是菱形.
3.已知:如图,在□ ABCD中,对角线AC与BD相交于点O,AB=,OA=2,OB=1.求证:□ ABCD是菱形.
证明:在△AOB中,
∵AB=,OA=2,OB=1,
∴AB =OA +OB .
∴△AOB是直角三角形,∠AOB是直角.
∴AC⊥BD.
∴□ ABCD是菱形.
菱形的判定
判定1
判定3
有一组邻边相等的平行四边形是菱形
判定2
四条边相等的四边形是菱形
对角线互相垂直的平行四边形是菱形
18.2.2.2 菱形的判定
1.掌握菱形的判定及证明过程.
2.能熟练运用菱形的判定进行计算和证明.
有一组邻边相等的平行四边形叫做菱形.
是轴对称图形,对角线所在的直线是对称轴.
四条边相等.
对角线互相垂直.
菱形的性质
对角线互相平分.
对角相等.
对边平行且相等.
菱形是如何定义的?菱形有哪些性质?
根据菱形的定义,可得菱形的第一个判定的方法:
AB=AD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
有一组邻边相等的平行四边形是菱形.
除此之外,你认为还有什么条件可以判断一个平行四边形是菱形?先想一想,再与同伴交流.
B
A
C
D
符号语言:
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.转动木条,这个平行四边形什么时候变成菱形
可以发现,对角线互相垂直的平行四边形是菱形.
下面我们证明这个结论.
已知:如图,在□ABCD中,对角线AC与BD相交于点O,AC⊥BD.
求证:□ ABCD是菱形.
判定定理 对角线互相垂直的平行四边形是菱形.
证明:∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线,∴BA=BC.
∴四边形ABCD是菱形.
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
A
C
B
D
你是怎么做的?你认为上述做法正确吗?与同伴交流.
如图,分别以A,C为圆心,
以大于AC的长为半径作弧,
两条弧分别相交于点B,D,
依次连接A,B,C,D,
四边形ABCD看上去是菱形.
判定定理 四条边相等的四边形是菱形.
由前面的探究可以得到定理如下:
请你完成这个定理的证明.
A
B
C
D
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:∵AB=BC=CD=AD,
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又AB=BC,
∴四边形ABCD是菱形.
你能用折纸的办法得到一个菱形吗?动手试一试!
先将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,将纸展开,就得到了一个菱形.
展开
你能说说这样做的道理吗?
因为四边相等的四边形是菱形.
例1 如图,在菱形ABCD中,对角线AC, BD相交于点O,点E,F,G,H 分别是OA,OB,OC,OD的中点.
求证:四边形EFGH是菱形.
D
A
B
C
O
E
F
G
H
分析:利用三角形的中位线定理,证明四边形EFGH的四条边相等即可.
证明: ∵四边形ABCD是菱形,
∴ AB=BC=CD=AD.
∵点E,F,G,H分别是OA,OB,OC,OD的中点,
∴EF,FG,GH,EH分别是△AOB, △BOC, △COD, △AOD的中位线,
∴ EF=AB,FG=BC,GH=CD,EH=AD,
∴EF=FG=GH=EH,
∴四边形EFGH是菱形.
D
A
B
C
O
E
F
G
H
例2 如图,在□ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF. 求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,
∴ AD=BC, AD//BC.
∵ DE=BF, ∴ AE=CF.
又AE//CF, ∴四边形AECF是平行四边形.
A
B
C
D
E
F
∵ AC⊥EF,
∴四边形AECF是菱形.
1.如图所示,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,两弧相交于点C,D,则直线CD即为所求.连接AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形
C.正方形 D.等腰梯形
解析:由题意知AC=AD=BD=BC,
∴四边形ADBC一定是菱形.
B
2.如图,AD是△ABC的一条角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.求证:四边形AEDF是菱形.
证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,∠EDA=∠DAF.
∵AD是△ABC的一条角平分线,
∴∠EAD=∠DAF.
∴∠EDA=∠EAD,
∴EA=ED.
∴四边形AEDF是菱形.
3.已知:如图,在□ ABCD中,对角线AC与BD相交于点O,AB=,OA=2,OB=1.求证:□ ABCD是菱形.
证明:在△AOB中,
∵AB=,OA=2,OB=1,
∴AB =OA +OB .
∴△AOB是直角三角形,∠AOB是直角.
∴AC⊥BD.
∴□ ABCD是菱形.
菱形的判定
判定1
判定3
有一组邻边相等的平行四边形是菱形
判定2
四条边相等的四边形是菱形
对角线互相垂直的平行四边形是菱形
