19.1.1.2 函数 课件(共22张PPT)
文档属性
| 名称 | 19.1.1.2 函数 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 957.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
第十九章 一次函数
19.1.1.2 函数
1.了解函数的相关概念,会判断两个变量是否具有函数关系.
2.能根据简单的实际问题写出函数解析式,并确定自变量的取值范围.
3.会根据函数解析式求函数值.
思考:
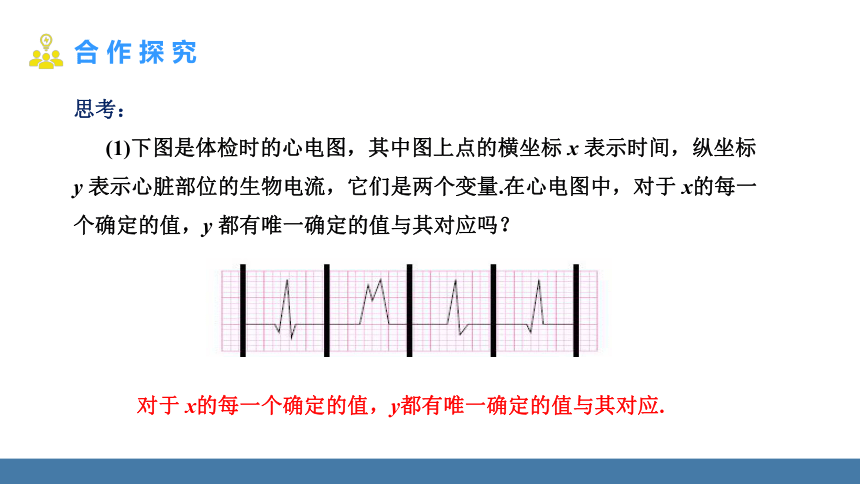
(1)下图是体检时的心电图,其中图上点的横坐标 x 表示时间,纵坐标y 表示心脏部位的生物电流,它们是两个变量.在心电图中,对于 x的每一个确定的值,y 都有唯一确定的值与其对应吗?
对于 x的每一个确定的值,y都有唯一确定的值与其对应.
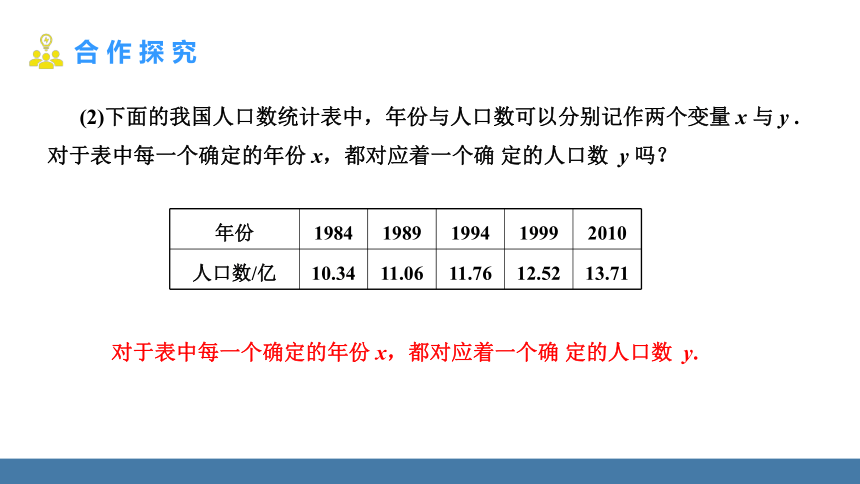
(2)下面的我国人口数统计表中,年份与人口数可以分别记作两个变量 x 与 y . 对于表中每一个确定的年份 x,都对应着一个确 定的人口数 y 吗?
年份 1984 1989 1994 1999 2010
人口数/亿 10.34 11.06 11.76 12.52 13.71
对于表中每一个确定的年份 x,都对应着一个确 定的人口数 y.
一般地,在一个变化过程中,如果有两个变量 x 与 y ,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x的函数.如果当 x=a 时 y=b,那么 b 叫做当自变量的值为 a 时的函数值.
特别提醒:
函数的定义中包括了对应值的存在性和唯一性两重意思,即对自变量的每一个确定的值,函数有且只有一个值与之对应,对自变量x的不同值,y的值可以相同,如:函数y=x2,当x=1和x=-1时,y的对应值都是 1.
回顾上节课的问题1,指出其中的函数关系和自变量,并举出函数值的例子.
时间 t 是自变量,路程 s 是 t 的函数.当 t =1 时,函数值 s =60,当 t =2 时,函数值 s =120.
在前面所给出的心电图和人口数统计表中,函数关系是怎样的?
在心电图中,时间x是自变量,心脏部位的生物电流y是x的函数;在人口数统计表中,年份x是自变量,人口数y是x的函数.
你能得出什么结论?
函数是刻画变量之间对应关系的数学模型,许多问题中变量之间的关系都可以用函数来表示.
A,B
例1 如图,各曲线中表示 y 是 x 的函数的是________.
A B C D
解析:要判断y是不是x的函数,关键看给x一个值,y是否也有一个唯一的值与其对应.若是,则y就是x的函数;若不是,则y就不是x的函数.
判断一个关系是否是函数关系的方法:一看是否存在于一个变化过程中;二看过程中是否存在两个变量;三看对于一个变量每取一个确定的值,另一个变量是否都有唯一确定的值与之对应.三者必须同时满足.
例2 汽车油箱中有汽油50 L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1 L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3) 汽车行驶200 km时,油箱中还有多少汽油?
解: (1)行驶路程x是自变量,油箱中的油量y是x的函数,它们的关系为
y= 50-0.1x.
像 y= 50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数关系的常用方法,这种式子叫做函数的解析式.
在解决第(2)问之前,思考:如何确定实际问题中自变量的取值范围?
自变量的取值范围要使所给函数解析式有意义,而实际问题中的自变量取值,还应保证实际问题有意义.
解:(2)仅从式子y=50-0.1x看,x可以取任意实数.但是考虑到x代表的实际意义为行驶路程,因此x不能取负数.行驶中的耗油量为0.1x,它不能超过油箱中现有汽油量50,即0. 1x≤50.因此,自变量x的取值范围是0≤ x≤500.
例2 汽车油箱中有汽油50 L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1 L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3) 汽车行驶200 km时,油箱中还有多少汽油?
例2 汽车油箱中有汽油50 L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1 L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3) 汽车行驶200 km时,油箱中还有多少汽油?
解:(3)汽车行驶200 km时,油箱中的汽油量是函数y=50-0.1x在x=200时的函数值.将x=200 代入y=50-0.1x,得y=50-0.1×200=30.
汽车行驶200 km时,油箱中还有30 L汽油.
你能根据例 2 (3) 的解题过程,总结一下求函数值的方法吗?
求函数值时,要注意函数的对应关系,代入自变量的值计算时,
要按照函数中代数式指明的运算顺序计算,并结合相应的运算法则,
使运算简便;说函数值时,要说明自变量是多少时的函数值.
B
1.下列说法正确的是( )
A.变量 x,y 满足 y2=x,则 y 是 x 的函数
B.变量 x,y满足 x+3y=1,则 y 是 x 的函数
C.变量 x,y满足 |y| =x,则 y 是 x 的函数
D.在V= πr3中, 是常量,π,r是自变量,V是r的函数
2.油箱中有油 30 kg ,油从管道中匀速流出,1h 流完,则油箱中剩余油量Q(kg)与流出时间 t(min)之间的函数关系式是____________,自变量 t 的取值范围是_________.
0≤t≤60
3.已知某公司的推销员每月的基本工资是1 200元,每推销一件商品得奖金 50 元,则推销员每月的总收入 y (元)与推销商品量 x (件)之间的关系式是_______________.
y=1 200+50x
4.函数 y = 的自变量x的取值范围是_________________.
5.使函数 y = 有意义的自变量 x 的取值范围为
______________________.
x≥-2且x≠1
x≤ 且x≠0且x≠-2
6.据测定,海底扩张的速度是很缓慢的,在太平洋海底,某海沟的某处宽度为 100 米,其两侧的地壳向外扩张的速度是每年 6 厘米,假设海沟扩张速度恒定,扩张时间为 x 年,海沟的宽度为 y 米.
(1)写出海沟扩张时间 x 年与海沟的宽度 y 米之间的表达式;
(2)当海沟宽度 y 扩张到 400 米时,需要多少年
解:(1)根据题意得海沟增加的宽度为 0.06 x 米,
∴海沟扩张时间 x 年与海沟的宽度 y 米之间的表达式为 y=0.06x+100.
(2)当 y = 400 时,0.06x+100=400,解得x=5 000.
答:当海沟宽度 y 扩张到 400 米时,需要 5 000 年.
函数
概念
自变量
取值范围
函数值
对于每一个x的值,y都有唯一的值与其对应
1.使函数解析式有意义
2.符合实际意义
第十九章 一次函数
19.1.1.2 函数
1.了解函数的相关概念,会判断两个变量是否具有函数关系.
2.能根据简单的实际问题写出函数解析式,并确定自变量的取值范围.
3.会根据函数解析式求函数值.
思考:
(1)下图是体检时的心电图,其中图上点的横坐标 x 表示时间,纵坐标y 表示心脏部位的生物电流,它们是两个变量.在心电图中,对于 x的每一个确定的值,y 都有唯一确定的值与其对应吗?
对于 x的每一个确定的值,y都有唯一确定的值与其对应.
(2)下面的我国人口数统计表中,年份与人口数可以分别记作两个变量 x 与 y . 对于表中每一个确定的年份 x,都对应着一个确 定的人口数 y 吗?
年份 1984 1989 1994 1999 2010
人口数/亿 10.34 11.06 11.76 12.52 13.71
对于表中每一个确定的年份 x,都对应着一个确 定的人口数 y.
一般地,在一个变化过程中,如果有两个变量 x 与 y ,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x的函数.如果当 x=a 时 y=b,那么 b 叫做当自变量的值为 a 时的函数值.
特别提醒:
函数的定义中包括了对应值的存在性和唯一性两重意思,即对自变量的每一个确定的值,函数有且只有一个值与之对应,对自变量x的不同值,y的值可以相同,如:函数y=x2,当x=1和x=-1时,y的对应值都是 1.
回顾上节课的问题1,指出其中的函数关系和自变量,并举出函数值的例子.
时间 t 是自变量,路程 s 是 t 的函数.当 t =1 时,函数值 s =60,当 t =2 时,函数值 s =120.
在前面所给出的心电图和人口数统计表中,函数关系是怎样的?
在心电图中,时间x是自变量,心脏部位的生物电流y是x的函数;在人口数统计表中,年份x是自变量,人口数y是x的函数.
你能得出什么结论?
函数是刻画变量之间对应关系的数学模型,许多问题中变量之间的关系都可以用函数来表示.
A,B
例1 如图,各曲线中表示 y 是 x 的函数的是________.
A B C D
解析:要判断y是不是x的函数,关键看给x一个值,y是否也有一个唯一的值与其对应.若是,则y就是x的函数;若不是,则y就不是x的函数.
判断一个关系是否是函数关系的方法:一看是否存在于一个变化过程中;二看过程中是否存在两个变量;三看对于一个变量每取一个确定的值,另一个变量是否都有唯一确定的值与之对应.三者必须同时满足.
例2 汽车油箱中有汽油50 L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1 L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3) 汽车行驶200 km时,油箱中还有多少汽油?
解: (1)行驶路程x是自变量,油箱中的油量y是x的函数,它们的关系为
y= 50-0.1x.
像 y= 50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数关系的常用方法,这种式子叫做函数的解析式.
在解决第(2)问之前,思考:如何确定实际问题中自变量的取值范围?
自变量的取值范围要使所给函数解析式有意义,而实际问题中的自变量取值,还应保证实际问题有意义.
解:(2)仅从式子y=50-0.1x看,x可以取任意实数.但是考虑到x代表的实际意义为行驶路程,因此x不能取负数.行驶中的耗油量为0.1x,它不能超过油箱中现有汽油量50,即0. 1x≤50.因此,自变量x的取值范围是0≤ x≤500.
例2 汽车油箱中有汽油50 L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1 L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3) 汽车行驶200 km时,油箱中还有多少汽油?
例2 汽车油箱中有汽油50 L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1 L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3) 汽车行驶200 km时,油箱中还有多少汽油?
解:(3)汽车行驶200 km时,油箱中的汽油量是函数y=50-0.1x在x=200时的函数值.将x=200 代入y=50-0.1x,得y=50-0.1×200=30.
汽车行驶200 km时,油箱中还有30 L汽油.
你能根据例 2 (3) 的解题过程,总结一下求函数值的方法吗?
求函数值时,要注意函数的对应关系,代入自变量的值计算时,
要按照函数中代数式指明的运算顺序计算,并结合相应的运算法则,
使运算简便;说函数值时,要说明自变量是多少时的函数值.
B
1.下列说法正确的是( )
A.变量 x,y 满足 y2=x,则 y 是 x 的函数
B.变量 x,y满足 x+3y=1,则 y 是 x 的函数
C.变量 x,y满足 |y| =x,则 y 是 x 的函数
D.在V= πr3中, 是常量,π,r是自变量,V是r的函数
2.油箱中有油 30 kg ,油从管道中匀速流出,1h 流完,则油箱中剩余油量Q(kg)与流出时间 t(min)之间的函数关系式是____________,自变量 t 的取值范围是_________.
0≤t≤60
3.已知某公司的推销员每月的基本工资是1 200元,每推销一件商品得奖金 50 元,则推销员每月的总收入 y (元)与推销商品量 x (件)之间的关系式是_______________.
y=1 200+50x
4.函数 y = 的自变量x的取值范围是_________________.
5.使函数 y = 有意义的自变量 x 的取值范围为
______________________.
x≥-2且x≠1
x≤ 且x≠0且x≠-2
6.据测定,海底扩张的速度是很缓慢的,在太平洋海底,某海沟的某处宽度为 100 米,其两侧的地壳向外扩张的速度是每年 6 厘米,假设海沟扩张速度恒定,扩张时间为 x 年,海沟的宽度为 y 米.
(1)写出海沟扩张时间 x 年与海沟的宽度 y 米之间的表达式;
(2)当海沟宽度 y 扩张到 400 米时,需要多少年
解:(1)根据题意得海沟增加的宽度为 0.06 x 米,
∴海沟扩张时间 x 年与海沟的宽度 y 米之间的表达式为 y=0.06x+100.
(2)当 y = 400 时,0.06x+100=400,解得x=5 000.
答:当海沟宽度 y 扩张到 400 米时,需要 5 000 年.
函数
概念
自变量
取值范围
函数值
对于每一个x的值,y都有唯一的值与其对应
1.使函数解析式有意义
2.符合实际意义
