19.1.2.3 函数的表示方法 课件(共21张PPT)
文档属性
| 名称 | 19.1.2.3 函数的表示方法 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 834.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 18:01:30 | ||
图片预览






文档简介
(共21张PPT)
第十九章 一次函数
19.1.2.3 函数的表示方法
1.了解函数的三种表示方法及其优点.
2.能用适当的方式表示简单实际问题中的变量之间的函数关系.
3.能对函数关系进行分析,对变量的变化情况进行初步讨论.
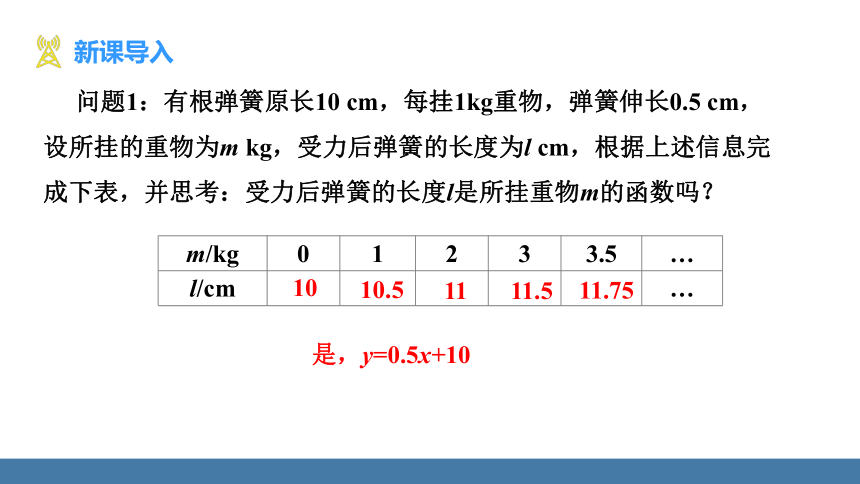
问题1:有根弹簧原长10 cm,每挂1kg重物,弹簧伸长0.5 cm,设所挂的重物为m kg,受力后弹簧的长度为l cm,根据上述信息完成下表,并思考:受力后弹簧的长度l是所挂重物m的函数吗?
m/kg 0 1 2 3 3.5 …
l/cm …
11.75
11.5
11
10.5
10
是,y=0.5x+10
问题2:有一辆出租车,前3公里内的起步价为8元,每超过1公里收2元,有一位乘客坐了t(t>3)公里,他付费y元.用含x的式子表示y,y是x的函数吗?
是,y=2x+2
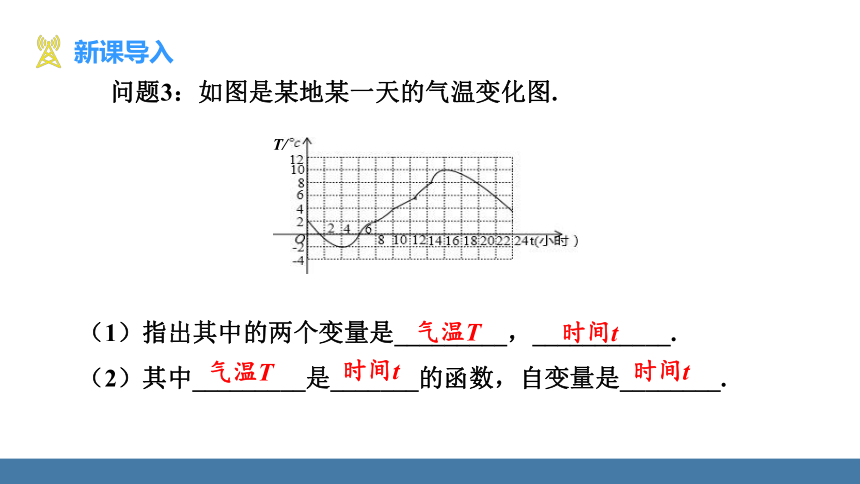
问题3:如图是某地某一天的气温变化图.
T/
(1)指出其中的两个变量是_________,___________.
(2)其中_________是_______的函数,自变量是________.
气温T
时间t
气温T
时间t
时间t
从上面的三个问题中,可以发现表示函数有哪三种方法?这三种表示函数的方法各有什么优点?
根据前面的三个问题,可以发现函数有三种表示方法,分别是解析式法,列表法和图象法.
1.解析式法:准确地反映了函数与自变量之间的数量关系.
2.列表法:具体地反映了函数与自变量的数值对应关系.
3.图象法:直观地反映了函数随自变量的变化而变化的规律.
表示函数时,要根据具体情况选择适当的方法,有时为全面地认识问题,需要同时使用几种方法.
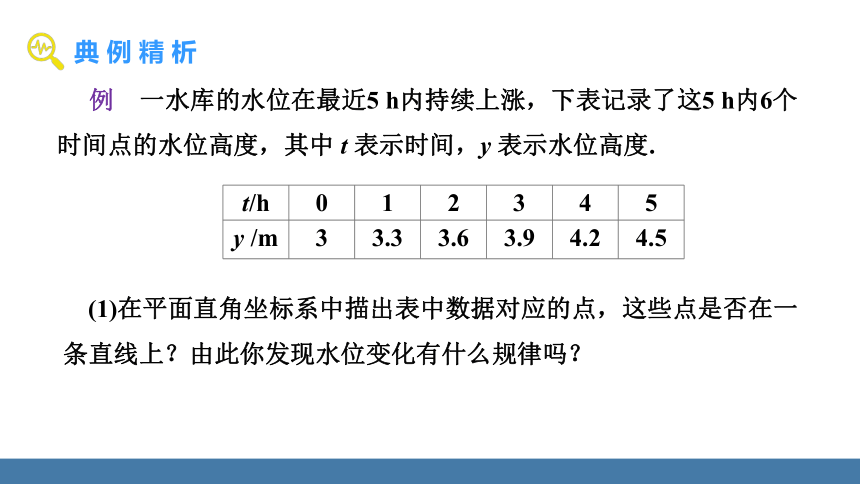
例 一水库的水位在最近5 h内持续上涨,下表记录了这5 h内6个时间点的水位高度,其中 t 表示时间,y 表示水位高度.
t/h 0 1 2 3 4 5
y /m 3 3.3 3.6 3.9 4.2 4.5
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律吗?
解: 如图,描出表中数据对应的点.可以看出,这6个点在一 条直线上.再结合表中数据,可以发现每小时水位上升0.3m.由此猜想,如果画出这5 h内其他时刻 (如t=2. 5 h等)及其水位高度所对应的点,它们可能也在这条直线上,即在这个时间段中水位可能是始终以同一速度均匀上升的.
O
1
x
y
1
2
3
4
5
4
3
2
5
A
B
(2)水位高度y是否为时间t的函数? 如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位的变化规律吗?
解:由于水位在最近5 h内持续上涨,对于时间 t的每一个确定的值,水位高度 y都有唯一的值与其对应,所以y是t的函数.开始时水位高度为3 m,以后每小时水位上升0.3 m.函数y=0. 3t+3(0≤t≤5)是符合表中数据的一个函数,它表示经过t h水位上升0.3t m,即水位y为(0. 3t+3)m.
O
1
x
y
1
2
3
4
5
4
3
2
5
A
B
其图象是右图中点A(0,3) 和点B(5,4.5)之间的线段AB.
(2)水位高度y是否为时间t的函数? 如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位的变化规律吗?
O
1
x
y
1
2
3
4
5
4
3
2
5
A
B
如果在这5 h内,水位一直匀速上升, 即升速为0.3m/h,那么函数y=0.3t+3(0≤t≤5)就精确地表示了这种变化规律.即使在这5 h内,水位的升速有些变化,而由于每小时水位上升0.3 m是确定的,因此这个函数也可以近似地表示水位的变化规律.
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将为多少米.
解:如果水位的变化规律不变,则可利用上述函数预测,
再过2 h,t=5+2=7(h)时,水位高度y=0. 3×7+3= 5.1(m).
本例说明三种函数表示方法之间有互补性,是可以相互转化的,体现了数形结合思想的应用.
并不是所有的函数都可以用这三种方法表示出来.如气温与时间的函数关系,只可用列表法和图象法表示,而无法用解析式法表示 .
在实际问题中,若纵轴和横轴上的点表示的是不同意义的量, 则两轴可以取不同单位长度,但每条坐标轴上的单位长度必须要一致.
特别需要注意的是不论用哪种表示方法都应使自变量的取值符合实际意义.
1.某省遭受台风袭击,大部分地区发生强降雨,某河受暴雨袭击,某天的水位记录如表,观察表中数据,水位上升最快的时段是( )
A. 8~12时 B.12~16时
C.16~20时 D.20~24时
时间/时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
D
2.用列表法与解析式法表示n边形的内角和m (单位:度)关于边数n的函数.
解:列表法:
多边形的边数n 3 4 5 6 …
内角和m 180° 360° 540° 720° …
解析式法:m=(n-2)·180°(n≥3,n为正整数).
3. 用解析式法与图象法表示等边三角形的周长l是边长a的函数.
解:∵等边三角形的周长l是边长a的3倍,
∴周长l与边长a的函数关系可表示为l=3a(a>0).
a … 1 2 3 4 …
l … 3 6 9 12 …
描点、连线:
列表:
O
2
x
y
1
2
3
4
8
6
4
10
12
4.甲车速度为20m/s,乙车速度为25m/s.现甲车在乙车前面500m,设x s后两车之间的距离为y m.求y随x(0≤x≤100)变化的函数解析式,并画出函数图象.
解:由题意可知,x s后两车行驶路程分别甲车为20x m,乙车为25x m,两车行驶路程差为25x-20x=5x(m),两车之间距离为(500-5x)m.所以y随x变化的函数关系式为y=500-5x (0≤x≤100).
描点、连线.
x … 10 20 30 40 … 100 …
y=500-5x … 450 400 350 300 … 0 …
用描点法画图,列表:
O
100
x
y
10
20
30
40
400
300
200
500
100
60
70
80
90
50
函数的表示方法
解析式法
图象法
列表法
函数与自变量之间的数量关系
函数与自变量的数值对应关系
函数随自变量的变化而
变化的规律
第十九章 一次函数
19.1.2.3 函数的表示方法
1.了解函数的三种表示方法及其优点.
2.能用适当的方式表示简单实际问题中的变量之间的函数关系.
3.能对函数关系进行分析,对变量的变化情况进行初步讨论.
问题1:有根弹簧原长10 cm,每挂1kg重物,弹簧伸长0.5 cm,设所挂的重物为m kg,受力后弹簧的长度为l cm,根据上述信息完成下表,并思考:受力后弹簧的长度l是所挂重物m的函数吗?
m/kg 0 1 2 3 3.5 …
l/cm …
11.75
11.5
11
10.5
10
是,y=0.5x+10
问题2:有一辆出租车,前3公里内的起步价为8元,每超过1公里收2元,有一位乘客坐了t(t>3)公里,他付费y元.用含x的式子表示y,y是x的函数吗?
是,y=2x+2
问题3:如图是某地某一天的气温变化图.
T/
(1)指出其中的两个变量是_________,___________.
(2)其中_________是_______的函数,自变量是________.
气温T
时间t
气温T
时间t
时间t
从上面的三个问题中,可以发现表示函数有哪三种方法?这三种表示函数的方法各有什么优点?
根据前面的三个问题,可以发现函数有三种表示方法,分别是解析式法,列表法和图象法.
1.解析式法:准确地反映了函数与自变量之间的数量关系.
2.列表法:具体地反映了函数与自变量的数值对应关系.
3.图象法:直观地反映了函数随自变量的变化而变化的规律.
表示函数时,要根据具体情况选择适当的方法,有时为全面地认识问题,需要同时使用几种方法.
例 一水库的水位在最近5 h内持续上涨,下表记录了这5 h内6个时间点的水位高度,其中 t 表示时间,y 表示水位高度.
t/h 0 1 2 3 4 5
y /m 3 3.3 3.6 3.9 4.2 4.5
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律吗?
解: 如图,描出表中数据对应的点.可以看出,这6个点在一 条直线上.再结合表中数据,可以发现每小时水位上升0.3m.由此猜想,如果画出这5 h内其他时刻 (如t=2. 5 h等)及其水位高度所对应的点,它们可能也在这条直线上,即在这个时间段中水位可能是始终以同一速度均匀上升的.
O
1
x
y
1
2
3
4
5
4
3
2
5
A
B
(2)水位高度y是否为时间t的函数? 如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位的变化规律吗?
解:由于水位在最近5 h内持续上涨,对于时间 t的每一个确定的值,水位高度 y都有唯一的值与其对应,所以y是t的函数.开始时水位高度为3 m,以后每小时水位上升0.3 m.函数y=0. 3t+3(0≤t≤5)是符合表中数据的一个函数,它表示经过t h水位上升0.3t m,即水位y为(0. 3t+3)m.
O
1
x
y
1
2
3
4
5
4
3
2
5
A
B
其图象是右图中点A(0,3) 和点B(5,4.5)之间的线段AB.
(2)水位高度y是否为时间t的函数? 如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位的变化规律吗?
O
1
x
y
1
2
3
4
5
4
3
2
5
A
B
如果在这5 h内,水位一直匀速上升, 即升速为0.3m/h,那么函数y=0.3t+3(0≤t≤5)就精确地表示了这种变化规律.即使在这5 h内,水位的升速有些变化,而由于每小时水位上升0.3 m是确定的,因此这个函数也可以近似地表示水位的变化规律.
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将为多少米.
解:如果水位的变化规律不变,则可利用上述函数预测,
再过2 h,t=5+2=7(h)时,水位高度y=0. 3×7+3= 5.1(m).
本例说明三种函数表示方法之间有互补性,是可以相互转化的,体现了数形结合思想的应用.
并不是所有的函数都可以用这三种方法表示出来.如气温与时间的函数关系,只可用列表法和图象法表示,而无法用解析式法表示 .
在实际问题中,若纵轴和横轴上的点表示的是不同意义的量, 则两轴可以取不同单位长度,但每条坐标轴上的单位长度必须要一致.
特别需要注意的是不论用哪种表示方法都应使自变量的取值符合实际意义.
1.某省遭受台风袭击,大部分地区发生强降雨,某河受暴雨袭击,某天的水位记录如表,观察表中数据,水位上升最快的时段是( )
A. 8~12时 B.12~16时
C.16~20时 D.20~24时
时间/时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
D
2.用列表法与解析式法表示n边形的内角和m (单位:度)关于边数n的函数.
解:列表法:
多边形的边数n 3 4 5 6 …
内角和m 180° 360° 540° 720° …
解析式法:m=(n-2)·180°(n≥3,n为正整数).
3. 用解析式法与图象法表示等边三角形的周长l是边长a的函数.
解:∵等边三角形的周长l是边长a的3倍,
∴周长l与边长a的函数关系可表示为l=3a(a>0).
a … 1 2 3 4 …
l … 3 6 9 12 …
描点、连线:
列表:
O
2
x
y
1
2
3
4
8
6
4
10
12
4.甲车速度为20m/s,乙车速度为25m/s.现甲车在乙车前面500m,设x s后两车之间的距离为y m.求y随x(0≤x≤100)变化的函数解析式,并画出函数图象.
解:由题意可知,x s后两车行驶路程分别甲车为20x m,乙车为25x m,两车行驶路程差为25x-20x=5x(m),两车之间距离为(500-5x)m.所以y随x变化的函数关系式为y=500-5x (0≤x≤100).
描点、连线.
x … 10 20 30 40 … 100 …
y=500-5x … 450 400 350 300 … 0 …
用描点法画图,列表:
O
100
x
y
10
20
30
40
400
300
200
500
100
60
70
80
90
50
函数的表示方法
解析式法
图象法
列表法
函数与自变量之间的数量关系
函数与自变量的数值对应关系
函数随自变量的变化而
变化的规律
