人教版八年级数学下册课件 19.2.1.2 正比例函数的图象与性质
文档属性
| 名称 | 人教版八年级数学下册课件 19.2.1.2 正比例函数的图象与性质 |

|
|
| 格式 | pptx | ||
| 文件大小 | 886.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第十九章 一次函数
19.2.1.2 正比例函数的图象与性质
1.理解正比例函数的图象的特点,会利用两点法画正比例函数的图象.
2.掌握正比例函数的性质,并能灵活运用解答有关问题.
列表
描点
连线
描点法画函数图象的三个步骤是_______、_______、_______.
本节课,我们研究正比例函数的图象,包括函数图象的画法和性质.
例1 画出下列正比例函数的图象:
(1)y=2x, ;(2)y=-1.5x,y=-4x.
解:函数y=2x中自变量x可为任意实数.
①列表如下:
x … -2 -1 0 1 2 …
y … -4 -2 0 2 4 …
y=2x
②描点;
③连线.
同样可以画出
函数 的图象.
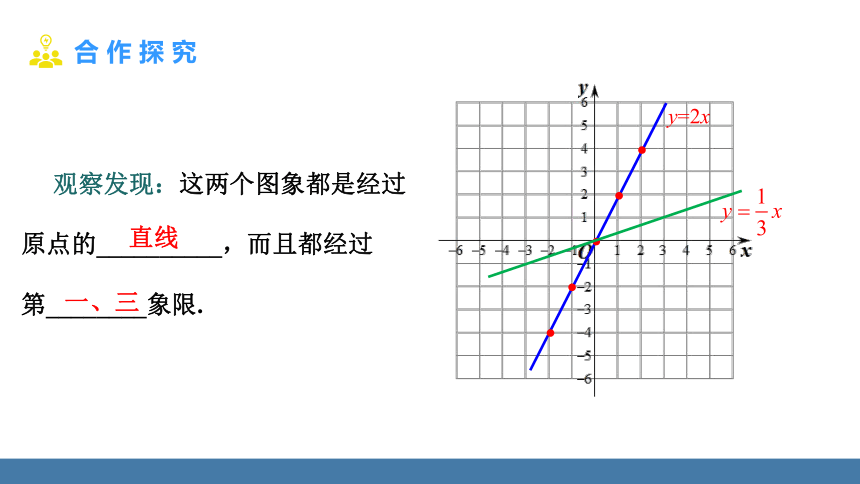
观察发现:这两个图象都是经过
原点的__________,而且都经过
第________象限.
一、三
直线
y=2x
x … -3 -2 -1 0 1 2 3 …
y … 4.5 3 1.5 0 -1.5 -3 -4.5 …
(2)y=-1.5x,y=-4x.
解:函数y=-1.5x中自变量x可为任意实数.
列表如下:
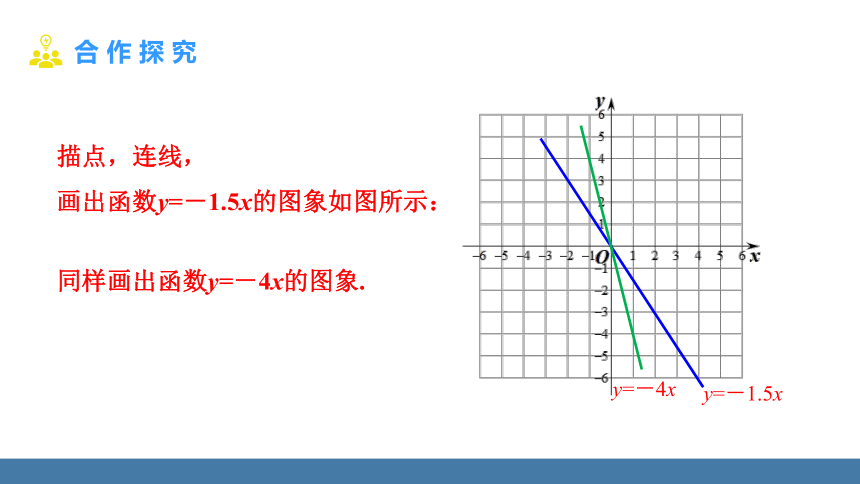
描点,连线,
画出函数y=-1.5x的图象如图所示:
y=-4x
y=-1.5x
同样画出函数y=-4x的图象.
y=-4x
y=-1.5x
发现:这两个函数图象都是经过原点和第_________象限的直线.
二、四
y=kx (k是常数,k≠0)的图象是一条经过原点的直线 y=kx(k≠0) 经过的象限
k>0
k<0
第一、三象限
第二、四象限
问题:在函数y=x , y=3x, y=- x和 y=-4x 中,随着x的增大,y的值分别如何变化
分析:对于函数y=x,当x=-1时,y=________;当x=1时,y=________;当x=2时,y=_______;不难发现y的值随x的增大而_______.
-1
1
2
增大
我们还可以借助函数图象分析此问题.
观察图象可以发现:①直线y=x,y=3x向右逐渐________,即y的值随x的增大而增大;
②直线y=- x,y=-4x向右逐渐________,即y的值随x的增大而减小.
上升
下降
在正比例函数y=kx中:
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
正比例函数y=kx(k≠0)的性质
思考
经过原点与点(1,k) (k是常数,k≠0)的直线是哪个函数的图象?画正比例函数的图象时,怎样画最简单?为什么?
因为两点确定一条直线,所以可用两点法画正比例函数
y=kx(k≠0)的图象.一般地,过原点和点(1,k)(k是常数,k≠0)
的直线,即正比例函数y=kx(k≠0)的图象.
用你认为最简单的方法画出下列函数的图象.
x 0 1
y 0 1
2
x 0 1
y 0 _ 1
2
解:(1)列表:
(2)列表:
x
y
1
2
3
-1
-3
-2
O
-1
-3
-2
1
2
3
画出两个函数图象如图所示:
特别提醒:
用两点法画函数图象时,(0,0)这点必选,因为图象过原点,而 (1,k)这点因函数关系式而定,选取时,最好使所选点的横、纵坐标均为整数,这样描点较容易 .
如果某函数图象是直线且经过原点(坐标轴除外),那么它对应的函数是正比例函数.
当k>0时,图象过第一、三象限;当k<0时,图象过第二、四象限.
已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1______y2(填“>”“<”或“=”).
解析:方法一:把点A、点B的坐标分别代入函数
y=3x,求出y1,y2的值比较大小即可.
方法二:画出正比例函数y=3x的图象,在函数图象上标出点A、点B,利用数形结合思想来比较y1,y2的大小.如图,观察图形,显然可得y1>y2.
>
方法三:根据正比例函数的增减性来比较函数值的大小.
根据正比例函数的性质,当k>0时,y随x的增大而增大,
即可得y1>y2.
已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1______y2(填“>”“<”或“=”).
>
正比例函数图象上两点的纵坐标的大小与比例系数及自变量的大小有关.比例系数是正数时,函数值随自变量的增大而增大;比例系数是负数时,函数值随自变量的增大而减小.本例的解法中,方法一是利用求值比较法;方法二是利用数形结合思想,用“形”上的点的位置来比较“数”的大小;方法三是利用函数的增减性来比较大小.
1.已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )
A.k>5 B.k<5
C.k>-5 D.k<-5
D
2.当x>0时,y与x的函数解析式为y=2x,当x≤0时,y与x的函数解析式为y=-2x,则在同一直角坐标系中的图象大致为( )
C
3.关于函数y=-2x,下列判断正确的是( )
A.图象经过第一、三象限
B.y随x的增大而增大
C.若(x1,y1),(x2,y2)是该函数图象上的两点,则当x1y2
D.不论x为何值,总有y<0
C
a<c<b
4.如图,三个正比例函数的图象分别对应解析式:①y=ax;②y=bx;③y=cx,将a,b,c从小到大排列并用“<”连接为___________.
5.若正比例函数y=(1-2m)x的图象经过第一、第三象限,则m的取值范围是___________.
6.已知函数y=kx(k≠0)的图象经过点P(-3,3),则k=________,图象经过第 象限.
二、四
-1
正比例函数的图象与性质
图象
性质
一条过原点的直线
k>0,经过第一、三象限,
y随着x的增大而增大
k<0,经过第二、四象限,
y随着x的增大而减小
第十九章 一次函数
19.2.1.2 正比例函数的图象与性质
1.理解正比例函数的图象的特点,会利用两点法画正比例函数的图象.
2.掌握正比例函数的性质,并能灵活运用解答有关问题.
列表
描点
连线
描点法画函数图象的三个步骤是_______、_______、_______.
本节课,我们研究正比例函数的图象,包括函数图象的画法和性质.
例1 画出下列正比例函数的图象:
(1)y=2x, ;(2)y=-1.5x,y=-4x.
解:函数y=2x中自变量x可为任意实数.
①列表如下:
x … -2 -1 0 1 2 …
y … -4 -2 0 2 4 …
y=2x
②描点;
③连线.
同样可以画出
函数 的图象.
观察发现:这两个图象都是经过
原点的__________,而且都经过
第________象限.
一、三
直线
y=2x
x … -3 -2 -1 0 1 2 3 …
y … 4.5 3 1.5 0 -1.5 -3 -4.5 …
(2)y=-1.5x,y=-4x.
解:函数y=-1.5x中自变量x可为任意实数.
列表如下:
描点,连线,
画出函数y=-1.5x的图象如图所示:
y=-4x
y=-1.5x
同样画出函数y=-4x的图象.
y=-4x
y=-1.5x
发现:这两个函数图象都是经过原点和第_________象限的直线.
二、四
y=kx (k是常数,k≠0)的图象是一条经过原点的直线 y=kx(k≠0) 经过的象限
k>0
k<0
第一、三象限
第二、四象限
问题:在函数y=x , y=3x, y=- x和 y=-4x 中,随着x的增大,y的值分别如何变化
分析:对于函数y=x,当x=-1时,y=________;当x=1时,y=________;当x=2时,y=_______;不难发现y的值随x的增大而_______.
-1
1
2
增大
我们还可以借助函数图象分析此问题.
观察图象可以发现:①直线y=x,y=3x向右逐渐________,即y的值随x的增大而增大;
②直线y=- x,y=-4x向右逐渐________,即y的值随x的增大而减小.
上升
下降
在正比例函数y=kx中:
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
正比例函数y=kx(k≠0)的性质
思考
经过原点与点(1,k) (k是常数,k≠0)的直线是哪个函数的图象?画正比例函数的图象时,怎样画最简单?为什么?
因为两点确定一条直线,所以可用两点法画正比例函数
y=kx(k≠0)的图象.一般地,过原点和点(1,k)(k是常数,k≠0)
的直线,即正比例函数y=kx(k≠0)的图象.
用你认为最简单的方法画出下列函数的图象.
x 0 1
y 0 1
2
x 0 1
y 0 _ 1
2
解:(1)列表:
(2)列表:
x
y
1
2
3
-1
-3
-2
O
-1
-3
-2
1
2
3
画出两个函数图象如图所示:
特别提醒:
用两点法画函数图象时,(0,0)这点必选,因为图象过原点,而 (1,k)这点因函数关系式而定,选取时,最好使所选点的横、纵坐标均为整数,这样描点较容易 .
如果某函数图象是直线且经过原点(坐标轴除外),那么它对应的函数是正比例函数.
当k>0时,图象过第一、三象限;当k<0时,图象过第二、四象限.
已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1______y2(填“>”“<”或“=”).
解析:方法一:把点A、点B的坐标分别代入函数
y=3x,求出y1,y2的值比较大小即可.
方法二:画出正比例函数y=3x的图象,在函数图象上标出点A、点B,利用数形结合思想来比较y1,y2的大小.如图,观察图形,显然可得y1>y2.
>
方法三:根据正比例函数的增减性来比较函数值的大小.
根据正比例函数的性质,当k>0时,y随x的增大而增大,
即可得y1>y2.
已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1______y2(填“>”“<”或“=”).
>
正比例函数图象上两点的纵坐标的大小与比例系数及自变量的大小有关.比例系数是正数时,函数值随自变量的增大而增大;比例系数是负数时,函数值随自变量的增大而减小.本例的解法中,方法一是利用求值比较法;方法二是利用数形结合思想,用“形”上的点的位置来比较“数”的大小;方法三是利用函数的增减性来比较大小.
1.已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )
A.k>5 B.k<5
C.k>-5 D.k<-5
D
2.当x>0时,y与x的函数解析式为y=2x,当x≤0时,y与x的函数解析式为y=-2x,则在同一直角坐标系中的图象大致为( )
C
3.关于函数y=-2x,下列判断正确的是( )
A.图象经过第一、三象限
B.y随x的增大而增大
C.若(x1,y1),(x2,y2)是该函数图象上的两点,则当x1
D.不论x为何值,总有y<0
C
a<c<b
4.如图,三个正比例函数的图象分别对应解析式:①y=ax;②y=bx;③y=cx,将a,b,c从小到大排列并用“<”连接为___________.
5.若正比例函数y=(1-2m)x的图象经过第一、第三象限,则m的取值范围是___________.
6.已知函数y=kx(k≠0)的图象经过点P(-3,3),则k=________,图象经过第 象限.
二、四
-1
正比例函数的图象与性质
图象
性质
一条过原点的直线
k>0,经过第一、三象限,
y随着x的增大而增大
k<0,经过第二、四象限,
y随着x的增大而减小
