19.2.2.3 待定系数法求一次函数解析式 课件(共17张PPT)
文档属性
| 名称 | 19.2.2.3 待定系数法求一次函数解析式 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 839.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第十九章 一次函数
19.2.2.3 待定系数法求一次函数解析式
1.理解待定系数法的意义.
2.会用待定系数法求一次函数的解析式.
前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考:
反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
两点法——两点确定一条直线
已知一次函数的图象过点(3, 5)与(-4,-9),求这个一次函数的解析式.
分析:求一次函数y=kx+b的解析式,关 键是求出k,b的值.
从已知条件可以列出关于k,b的二元一次方程组,并求出k,b.
解:设这个一次函数的解析式为y=kx+b(k≠0).
因为y=kx+b的图象过点(3, 5)与(-4,-9),
所以 解方程组得
这个一次函数的解析式为y=2x-1.
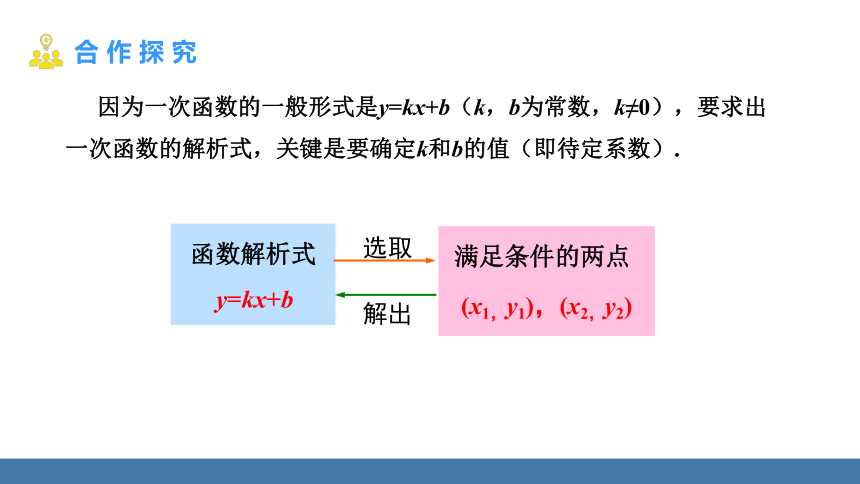
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的解析式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
选取
解出
先假定解析式中的未知系数,然后根据已知条件求出待定的系数,从而确定出该解析式的方法是数学上常用的方法,这种方法称为待定系数法.
(1)设:设一次函数的一般形式 _______________;
(3)解:解二元一次方程组得k, b;
(4)还原:把k,b的值代入一次函数的解析式.
用待定系数法求一次函数解析式的步骤:
(2)列:把图象上的点 , 代入一次函数的解析式,组成_________方程组;
y=kx+b(k≠0)
二元一次
特别提醒:
用待定系数法求函数解析式时,要先判断函数是哪一类函数,然后才能设出所求函数的解析式 .
在正比例函数y=kx中,只有一个待定系数k,只需要一个除 (0,0)外的条件即可求出k的值;在一次函数y=kx+b中,有两个待定系数k,b,因而需要两个条件才能求出k 和 b 的值 .
例 已知一次函数的图象经过点(9,0)和点(24,20),写出函数解析式.
解:设一次函数解析式为y=kx+b.
则 解得
所以一次函数解析式为y= x-12.
用待定系数法确定函数解析式时,应注意结合题目信息,根据不同情况选择相应方法:
(1)如果已知图象经过点的坐标,那么可直接构造方程(组)求解;
(2)当直线经过的点的坐标未知时,结合题意,先确定直线经过的点的坐标,再构造方程(组)求解.
1.正比例函数y=kx经过点(-1,2),则它的函数解析式为 .
2.一次函数的图象经过点(1,-1),(-2,5),则一次函数的解析式为 .
3.已知一次函数y=-x+b的图象过点(8,2),则此一次函数的解析式为 .
y=-x+10
y=-2x+1
y=-2x
4. 如图,直线l是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
2
-18
-42
l
y
x
5.已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4.求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b(k≠0),
将x=3,y=1和x=-2,y=-4分别代入上式
得 解得
所以这个一次函数的解析式为y=x-2.
6.一次函数y=kx+4的图象经过点(-3,-2).
(1)求这个函数的解析式;(2)判断(-5,3)是否在此函数的图象上.
解:(1)把(-3,-2)代入解析式,得-3k+4=-2,解得k=2,
∴解析式为y=2x+4.
(2)把x=-5代入解析式,得y=2×(-5)+4=-6≠3,
因而(-5,3)不在此函数的图象上.
求一次函数
解析式
待定系数法
1设
2列
3解
4写
第十九章 一次函数
19.2.2.3 待定系数法求一次函数解析式
1.理解待定系数法的意义.
2.会用待定系数法求一次函数的解析式.
前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考:
反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
两点法——两点确定一条直线
已知一次函数的图象过点(3, 5)与(-4,-9),求这个一次函数的解析式.
分析:求一次函数y=kx+b的解析式,关 键是求出k,b的值.
从已知条件可以列出关于k,b的二元一次方程组,并求出k,b.
解:设这个一次函数的解析式为y=kx+b(k≠0).
因为y=kx+b的图象过点(3, 5)与(-4,-9),
所以 解方程组得
这个一次函数的解析式为y=2x-1.
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的解析式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
选取
解出
先假定解析式中的未知系数,然后根据已知条件求出待定的系数,从而确定出该解析式的方法是数学上常用的方法,这种方法称为待定系数法.
(1)设:设一次函数的一般形式 _______________;
(3)解:解二元一次方程组得k, b;
(4)还原:把k,b的值代入一次函数的解析式.
用待定系数法求一次函数解析式的步骤:
(2)列:把图象上的点 , 代入一次函数的解析式,组成_________方程组;
y=kx+b(k≠0)
二元一次
特别提醒:
用待定系数法求函数解析式时,要先判断函数是哪一类函数,然后才能设出所求函数的解析式 .
在正比例函数y=kx中,只有一个待定系数k,只需要一个除 (0,0)外的条件即可求出k的值;在一次函数y=kx+b中,有两个待定系数k,b,因而需要两个条件才能求出k 和 b 的值 .
例 已知一次函数的图象经过点(9,0)和点(24,20),写出函数解析式.
解:设一次函数解析式为y=kx+b.
则 解得
所以一次函数解析式为y= x-12.
用待定系数法确定函数解析式时,应注意结合题目信息,根据不同情况选择相应方法:
(1)如果已知图象经过点的坐标,那么可直接构造方程(组)求解;
(2)当直线经过的点的坐标未知时,结合题意,先确定直线经过的点的坐标,再构造方程(组)求解.
1.正比例函数y=kx经过点(-1,2),则它的函数解析式为 .
2.一次函数的图象经过点(1,-1),(-2,5),则一次函数的解析式为 .
3.已知一次函数y=-x+b的图象过点(8,2),则此一次函数的解析式为 .
y=-x+10
y=-2x+1
y=-2x
4. 如图,直线l是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
2
-18
-42
l
y
x
5.已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4.求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b(k≠0),
将x=3,y=1和x=-2,y=-4分别代入上式
得 解得
所以这个一次函数的解析式为y=x-2.
6.一次函数y=kx+4的图象经过点(-3,-2).
(1)求这个函数的解析式;(2)判断(-5,3)是否在此函数的图象上.
解:(1)把(-3,-2)代入解析式,得-3k+4=-2,解得k=2,
∴解析式为y=2x+4.
(2)把x=-5代入解析式,得y=2×(-5)+4=-6≠3,
因而(-5,3)不在此函数的图象上.
求一次函数
解析式
待定系数法
1设
2列
3解
4写
