19.3 选择方案 课件(共23张PPT)
文档属性
| 名称 | 19.3 选择方案 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 855.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第十九章 一次函数
19.3 选择方案
1.会用一次函数知识解决方案选择问题,体会函数模型思想.
2.能从不同的角度思考问题,优化解决问题的方法.
3.能进行解决问题过程的反思,总结解决问题的方法.
做一件事情,有时有不同的实施方案.比较这些方案,从中选择最佳方案作为行动计划,是非常有必要的.在选择方案时,往往需要从数学角度进行分析,涉及变量的问题常用到函数.下面通过新课的学习,我们可以体会如何运用一次函数选择最佳方案.
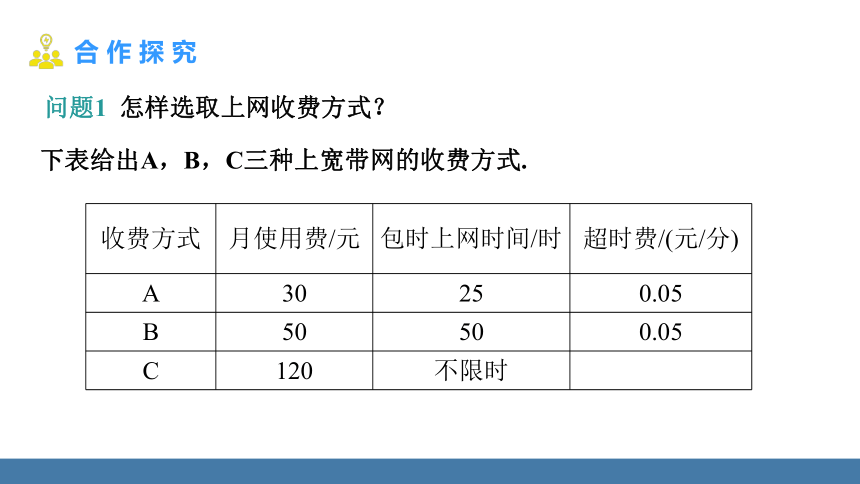
问题1 怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表给出A,B,C三种上宽带网的收费方式.
1.三种收费方式有什么区别?
2.在变化的收费方式中,上网费由哪些部分组成?
3.影响超时费的因素是什么?
4.这三种方式中有固定最优惠的方式吗?
A,B会变化,C不变.
上网费=月使用费+超时费
上网时间
没有,与上网的时间有关.
5.设月上网时间为x小时,则方案方式A,B的收费金额y1,y2都是x的函数,要比较上网费用,需在 x > 0 的条件下,考虑何时(1)y1 = y2,(2) y1 < y2, (3)y1 > y2.
利用函数解析式,通过方程、不等式或函数图象能解答上述问题.
在此基础上,再用其中省钱的方式与方式C进行比较,则容易对收费方式作出选择.
思考:在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
不一定,只有在上网时间超过25小时时才会产生.所以考虑收费金额时,要把上网时间分为25小时内和超过25小时两种情况.得到的函数如下:
问题:你能写出方式B,C的收费金额y2,y3关于上网时间 x的函数解析式吗?
当x≥0时,y3=120.
分别写出函数解析式如下:
在同一坐标系画出它们的图象:
当上网时间__________时,选择方式A最省钱.
当上网时间_____________时,选择方式B最省钱.
当上网时间_________时,选择方式C最省钱.
问题2 怎样租车?
某学校计划在总费用2 300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金 /(元/辆) 400 280
问题1:共有几种租车方案?
共三种:(1)单独租甲种车;(2)单独租乙种车;
(3)同时租甲种车和乙种车.
问题2:如果单独租甲种车需要多少辆?乙种车呢?
问题3:如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于6辆,不能超过8辆.
租用甲种车:240÷5=5 (辆),
租用乙种车:240÷30=8(辆).
单独租甲种车要6辆,单独租乙种车要8辆.
问题4:要使6名教师至少在每辆车上有1名,你能确定排除哪种方案?你能确定租车的辆数吗?
说明了车辆总数不会超过6,可以排除单独租乙种车的方案,所以租车的辆数只能为6.
思考:合租甲、乙两种车的时候,又有很多种方案可供选择,应该如何选出最节省费用的租车方案呢?
租车费用与所租车的种类有关.可以看出,当汽车总数a确定后,在满足各项要求的前提下,尽可能少地租用甲种客车可以节省费用.
设租用x辆甲种客车,则租车费用y是x的函数,即y=400x+280(a-x).
将已经确定的a的值带入,化简这个函数,得y=120x+1 680.
(1)为使240名师生有车坐,可以确定x的一个范围吗?
(2)为使租车费用不超过2 300元,可以确定x的范围吗?
可以得到x的取值范围:4≤x≤5
结合前面所求出的x的取值范围,你能得出几种不同的租车方案?为节省费用应选择其中哪个方案?请说明理由.
方案1:当x=4时,即租用4辆甲种汽车,2辆乙种汽车,
y=120×4+1 680=2 160(元).
方案2:当x=5时,即租用5辆甲种汽车,1辆乙种汽车,
y=120×5+1 680=2 280(元).
所以应该选择方案1.
解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
1.如图是甲、乙两家商店销售同一种产品的销售价 y(元)与销售量 x(件)之间的函数图象.下列说法,其中正确的说法有 .(填序号)
①售2件时甲、乙两家售价一样;
②买1件时买乙家的合算;
③买3件时买甲家的合算;
④买1件时,售价约为3元.
①②③
2.某工厂有甲种原料130 kg,乙种原料144 kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5 kg,乙种原料4 kg,且每件A产品可获利700元;生产每件B产品需甲种原料3 kg,乙种原料6 kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种?
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
解:(1)根据题意得 解得18≤x≤20,
∵x是正整数,∴x=18,19,20.
共有三种方案:
方案一:生产A产品18件、B产品12件;
方案二:生产A产品19件、B产品11件;
方案三:生产A产品20件、B产品10件.
(2)根据题意得y=700x+900(30-x)=-200x+27 000,
∵-200<0,∴y随x的增大而减小.
∴当x=18时,y有最大值,
y最大=-200×18+27 000=23 400.
∴利润最大的方案是方案一:生产A产品18件、B产品12件,最大利润为23 400元.
解决方案问题
建立数学模型
确定自变量取值范围
利用函数增减性选出最佳方案
第十九章 一次函数
19.3 选择方案
1.会用一次函数知识解决方案选择问题,体会函数模型思想.
2.能从不同的角度思考问题,优化解决问题的方法.
3.能进行解决问题过程的反思,总结解决问题的方法.
做一件事情,有时有不同的实施方案.比较这些方案,从中选择最佳方案作为行动计划,是非常有必要的.在选择方案时,往往需要从数学角度进行分析,涉及变量的问题常用到函数.下面通过新课的学习,我们可以体会如何运用一次函数选择最佳方案.
问题1 怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表给出A,B,C三种上宽带网的收费方式.
1.三种收费方式有什么区别?
2.在变化的收费方式中,上网费由哪些部分组成?
3.影响超时费的因素是什么?
4.这三种方式中有固定最优惠的方式吗?
A,B会变化,C不变.
上网费=月使用费+超时费
上网时间
没有,与上网的时间有关.
5.设月上网时间为x小时,则方案方式A,B的收费金额y1,y2都是x的函数,要比较上网费用,需在 x > 0 的条件下,考虑何时(1)y1 = y2,(2) y1 < y2, (3)y1 > y2.
利用函数解析式,通过方程、不等式或函数图象能解答上述问题.
在此基础上,再用其中省钱的方式与方式C进行比较,则容易对收费方式作出选择.
思考:在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
不一定,只有在上网时间超过25小时时才会产生.所以考虑收费金额时,要把上网时间分为25小时内和超过25小时两种情况.得到的函数如下:
问题:你能写出方式B,C的收费金额y2,y3关于上网时间 x的函数解析式吗?
当x≥0时,y3=120.
分别写出函数解析式如下:
在同一坐标系画出它们的图象:
当上网时间__________时,选择方式A最省钱.
当上网时间_____________时,选择方式B最省钱.
当上网时间_________时,选择方式C最省钱.
问题2 怎样租车?
某学校计划在总费用2 300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车 乙种客车
载客量/(人/辆) 45 30
租金 /(元/辆) 400 280
问题1:共有几种租车方案?
共三种:(1)单独租甲种车;(2)单独租乙种车;
(3)同时租甲种车和乙种车.
问题2:如果单独租甲种车需要多少辆?乙种车呢?
问题3:如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于6辆,不能超过8辆.
租用甲种车:240÷5=5 (辆),
租用乙种车:240÷30=8(辆).
单独租甲种车要6辆,单独租乙种车要8辆.
问题4:要使6名教师至少在每辆车上有1名,你能确定排除哪种方案?你能确定租车的辆数吗?
说明了车辆总数不会超过6,可以排除单独租乙种车的方案,所以租车的辆数只能为6.
思考:合租甲、乙两种车的时候,又有很多种方案可供选择,应该如何选出最节省费用的租车方案呢?
租车费用与所租车的种类有关.可以看出,当汽车总数a确定后,在满足各项要求的前提下,尽可能少地租用甲种客车可以节省费用.
设租用x辆甲种客车,则租车费用y是x的函数,即y=400x+280(a-x).
将已经确定的a的值带入,化简这个函数,得y=120x+1 680.
(1)为使240名师生有车坐,可以确定x的一个范围吗?
(2)为使租车费用不超过2 300元,可以确定x的范围吗?
可以得到x的取值范围:4≤x≤5
结合前面所求出的x的取值范围,你能得出几种不同的租车方案?为节省费用应选择其中哪个方案?请说明理由.
方案1:当x=4时,即租用4辆甲种汽车,2辆乙种汽车,
y=120×4+1 680=2 160(元).
方案2:当x=5时,即租用5辆甲种汽车,1辆乙种汽车,
y=120×5+1 680=2 280(元).
所以应该选择方案1.
解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
1.如图是甲、乙两家商店销售同一种产品的销售价 y(元)与销售量 x(件)之间的函数图象.下列说法,其中正确的说法有 .(填序号)
①售2件时甲、乙两家售价一样;
②买1件时买乙家的合算;
③买3件时买甲家的合算;
④买1件时,售价约为3元.
①②③
2.某工厂有甲种原料130 kg,乙种原料144 kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5 kg,乙种原料4 kg,且每件A产品可获利700元;生产每件B产品需甲种原料3 kg,乙种原料6 kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种?
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
解:(1)根据题意得 解得18≤x≤20,
∵x是正整数,∴x=18,19,20.
共有三种方案:
方案一:生产A产品18件、B产品12件;
方案二:生产A产品19件、B产品11件;
方案三:生产A产品20件、B产品10件.
(2)根据题意得y=700x+900(30-x)=-200x+27 000,
∵-200<0,∴y随x的增大而减小.
∴当x=18时,y有最大值,
y最大=-200×18+27 000=23 400.
∴利润最大的方案是方案一:生产A产品18件、B产品12件,最大利润为23 400元.
解决方案问题
建立数学模型
确定自变量取值范围
利用函数增减性选出最佳方案
