5.1.1 相交线 课件 (共12张PPT)
文档属性
| 名称 | 5.1.1 相交线 课件 (共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
第五章 相交线与平行线
5.1.1 相交线
1.了解邻补角、对顶角的概念,能找出图形中的一个角的邻补角和对顶角.
2.理解邻补角、对顶角的性质,并能够进行简单应用.
观察下面的图片,你能否看到相交线?
如果把相交的马路看成两条相交的直线,那么就出现了 的问题.
角
问题1:任意画两条相交的直线,所形成的4个角中,∠1和∠4有
怎样的位置关系?
A
B
C
D
O
4
1
2
3
∠1和∠4有一条公共边OC,它们的另一边
互为反向延长线,即∠1和∠4互补,具有
这种关系的两个角,互为邻补角.
∠1和∠2
∠2和∠3
∠3和∠4
你还能在图中找出其他的邻补角吗?
如图,直线AB和CD相交于点O,则∠AOC的邻补角是______________.
∠AOD和∠BOC
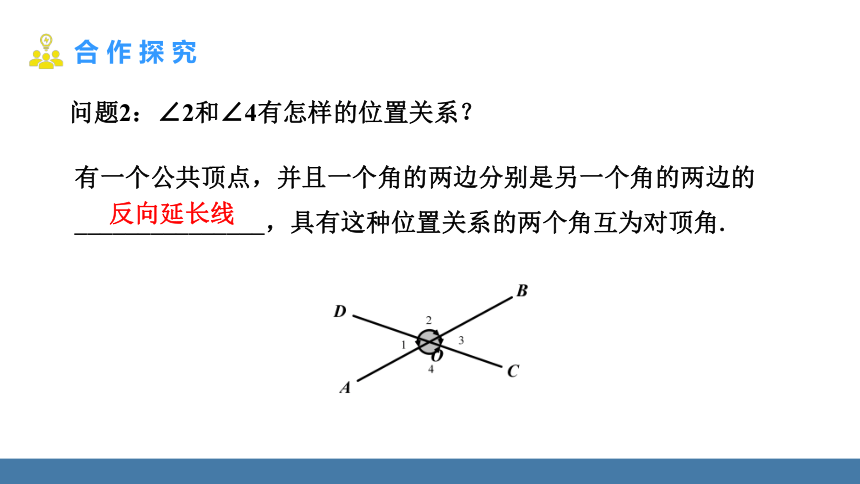
问题2:∠2和∠4有怎样的位置关系?
有一个公共顶点,并且一个角的两边分别是另一个角的两边的
_______________,具有这种位置关系的两个角互为对顶角.
反向延长线
下列各图中,∠1和∠2是对顶角吗?
1
2
1
2
2
1
不是
是
不是
∠1和∠4之间有怎样的数量关系?
A
B
C
D
O
4
1
2
3
因为∠1和∠4互为邻补角,所以∠1和∠4的数量关系是互补.
∠1和∠3之间又有怎样的数量关系?
因为∠1与∠2互补,∠3与∠2互补,
所以∠1=∠3(同角的补角相等),
同理∠2=∠4.
得到对顶角的性质:对顶角相等.
1.下面各图中∠1和∠2是对顶角的是( )
B
A B
C D
2.下列各图中,∠1与∠2互为邻补角的是( )
D
A B
C D
3.在括号内填写依据:
如图,因为直线a,b相交于点O,
所以∠1+∠3=180°( ),
∠1=∠2( ).
邻补角互补
对顶角相等
1.什么是邻补角?邻补角的性质是什么?
2.什么是对顶角?对顶角的性质是什么?
3.邻补角和对顶角的相同点与不同点是什么?
第五章 相交线与平行线
5.1.1 相交线
1.了解邻补角、对顶角的概念,能找出图形中的一个角的邻补角和对顶角.
2.理解邻补角、对顶角的性质,并能够进行简单应用.
观察下面的图片,你能否看到相交线?
如果把相交的马路看成两条相交的直线,那么就出现了 的问题.
角
问题1:任意画两条相交的直线,所形成的4个角中,∠1和∠4有
怎样的位置关系?
A
B
C
D
O
4
1
2
3
∠1和∠4有一条公共边OC,它们的另一边
互为反向延长线,即∠1和∠4互补,具有
这种关系的两个角,互为邻补角.
∠1和∠2
∠2和∠3
∠3和∠4
你还能在图中找出其他的邻补角吗?
如图,直线AB和CD相交于点O,则∠AOC的邻补角是______________.
∠AOD和∠BOC
问题2:∠2和∠4有怎样的位置关系?
有一个公共顶点,并且一个角的两边分别是另一个角的两边的
_______________,具有这种位置关系的两个角互为对顶角.
反向延长线
下列各图中,∠1和∠2是对顶角吗?
1
2
1
2
2
1
不是
是
不是
∠1和∠4之间有怎样的数量关系?
A
B
C
D
O
4
1
2
3
因为∠1和∠4互为邻补角,所以∠1和∠4的数量关系是互补.
∠1和∠3之间又有怎样的数量关系?
因为∠1与∠2互补,∠3与∠2互补,
所以∠1=∠3(同角的补角相等),
同理∠2=∠4.
得到对顶角的性质:对顶角相等.
1.下面各图中∠1和∠2是对顶角的是( )
B
A B
C D
2.下列各图中,∠1与∠2互为邻补角的是( )
D
A B
C D
3.在括号内填写依据:
如图,因为直线a,b相交于点O,
所以∠1+∠3=180°( ),
∠1=∠2( ).
邻补角互补
对顶角相等
1.什么是邻补角?邻补角的性质是什么?
2.什么是对顶角?对顶角的性质是什么?
3.邻补角和对顶角的相同点与不同点是什么?
