5.1.2 垂线 课件 (共18张PPT)
文档属性
| 名称 | 5.1.2 垂线 课件 (共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
第五章 相交线与平行线
5.1.2 垂线
1.理解垂线、垂线段的概念,掌握垂线的画法.
2.掌握垂线性质及应用.
3.理解点到直线的距离的意义.
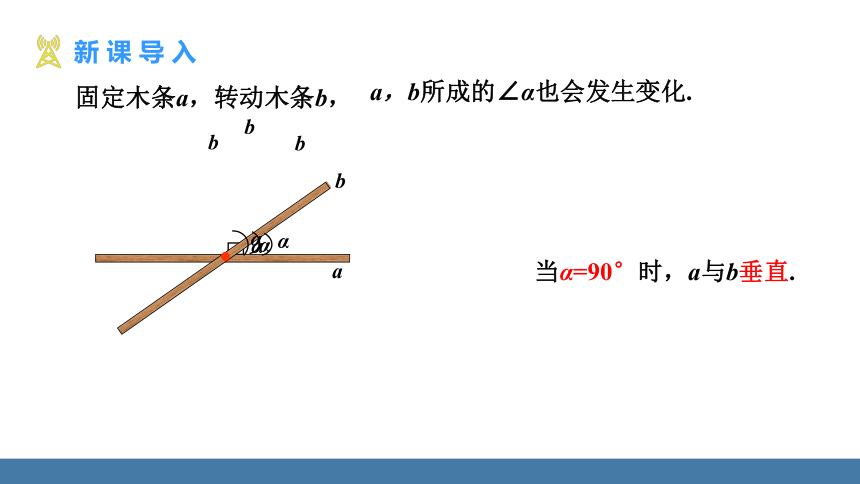
固定木条a,转动木条b,
α
a
b
当α=90°时,a与b垂直.
a,b所成的∠α也会发生变化.
α
α
α
b
b
b
当两条直线相交所成的四个角中,有 一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1.垂直及垂线
a与b相互垂直,
O叫垂足.
a叫b的垂线,b也叫a的垂线.
b
a
O
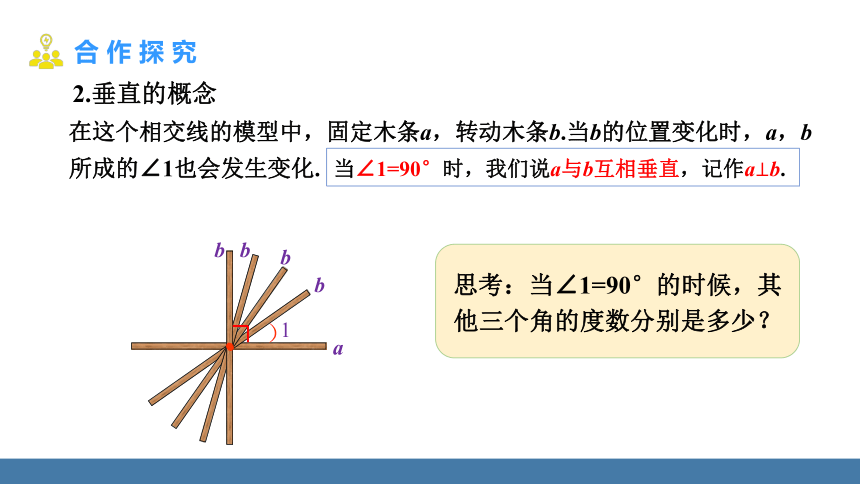
在这个相交线的模型中,固定木条a,转动木条b.当b的位置变化时,a,b所成的∠1也会发生变化.
)
1
a
b
思考:当∠1=90°的时候,其他三个角的度数分别是多少?
b
b
b
当∠1=90°时,我们说a与b互相垂直,记作ab.
2.垂直的概念
A
B
C
D
O
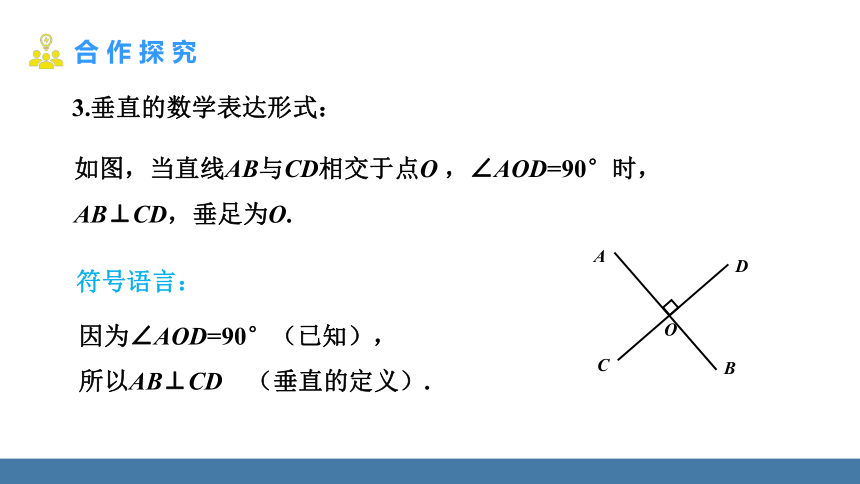
符号语言:
如图,当直线AB与CD相交于点O ,∠AOD=90°时,
AB⊥CD,垂足为O.
因为∠AOD=90°(已知),
所以AB⊥CD (垂直的定义).
3.垂直的数学表达形式:
符号语言:
反之,若直线AB与CD垂直,垂足为O,那么∠AOD=90°.
因为 AB⊥CD (已知),
所以 ∠AOD=90° (垂直的定义).
3.垂直的数学表达形式:
A
B
C
D
O
0
1
2
3
4
5
6
7
8
9
10
11
Cm
这样画l的垂线可以画几条?
1.放
2.靠
3.画线
l
如图,已知直线 l,作l的垂线.
工具:直尺、三角板
无数条
4.垂线的画法
O
A
l
A
如图,已知直线 l 和l外的一点A,过点A作l的垂线.
B
则所画直线AB是过点A的直线l的垂线.
0
1
2
3
4
5
6
7
8
9
10
11
Cm
4.垂线的画法
通过画图我们可以知道经过一点(已知直线上或直线外),
能画出已知直线的一条垂线,并且只能画出一条垂线.
即:在同一平面内,过一点有且只有一条直线与已知直线垂直.
“一落”即让三角形的一条直角边落在已知直线上;
“二移”即沿直线移动三角尺,使其另一直角边经过已知点;
“三画”即沿此直线边画直线,则这条直线就是已知直线的垂线.
垂线的画法
垂线的性质
例 如图,直线AB,CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.
解:因为 AB⊥OE (已知),
所以∠EOB=90°(垂直的定义).
因为 ∠BOD =∠1=55° (对顶角相等),
所以 ∠EOD =∠EOB +∠BOD
=90°+55°
=145°.
A
C
E
B
D
O
1
灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短?
我们可以将这条河看成一条直线l,从而将这个实际问题转化成数学问题.
l
简单说成:垂线段最短.
由直线外一点向直线引垂线,这点与垂足间的线段叫做垂线段.
P
l
A
5.垂线段
连接直线外一点与直线上各点的所有线段中,垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
P
l
A
6.点到直线的距离
2.如图,CD⊥AB, ∠ACB=90° ,线段AC,BC,CD中最短的是( )
A.AC B.CD C.BC D.不能确定
B
D
A
B
C
1.已知点A,与点A的距离是5cm的直线可画( )
A. 1条 B. 2条 C. 3条 D. 无数条
D
3.如图,过点P分别作OA,OB的垂线.
O
A
B
P
M
N
注意:过一点作已知线段(或射线)的垂线,
就是作这条线段(或射线)所在直线的垂线.
4.如图,直线AB,CD交于点O,EO⊥AB,垂足为O,∠EOC=35°,则∠AOD是多少度?
解:因为EO⊥AB,
所以∠BOE=90°.
又因为∠COE=35°,
所以∠COB=∠COE+∠BOE=125°.
因为∠AOD=∠COB(对顶角相等),
所以∠AOD=125°.
1.垂线:在同一平面内,过一点有且只有一条直线与已知直线垂直.
2.垂线段:连接直线外一点与直线上各点的所有线段中,垂线段最短.
3.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
第五章 相交线与平行线
5.1.2 垂线
1.理解垂线、垂线段的概念,掌握垂线的画法.
2.掌握垂线性质及应用.
3.理解点到直线的距离的意义.
固定木条a,转动木条b,
α
a
b
当α=90°时,a与b垂直.
a,b所成的∠α也会发生变化.
α
α
α
b
b
b
当两条直线相交所成的四个角中,有 一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
1.垂直及垂线
a与b相互垂直,
O叫垂足.
a叫b的垂线,b也叫a的垂线.
b
a
O
在这个相交线的模型中,固定木条a,转动木条b.当b的位置变化时,a,b所成的∠1也会发生变化.
)
1
a
b
思考:当∠1=90°的时候,其他三个角的度数分别是多少?
b
b
b
当∠1=90°时,我们说a与b互相垂直,记作ab.
2.垂直的概念
A
B
C
D
O
符号语言:
如图,当直线AB与CD相交于点O ,∠AOD=90°时,
AB⊥CD,垂足为O.
因为∠AOD=90°(已知),
所以AB⊥CD (垂直的定义).
3.垂直的数学表达形式:
符号语言:
反之,若直线AB与CD垂直,垂足为O,那么∠AOD=90°.
因为 AB⊥CD (已知),
所以 ∠AOD=90° (垂直的定义).
3.垂直的数学表达形式:
A
B
C
D
O
0
1
2
3
4
5
6
7
8
9
10
11
Cm
这样画l的垂线可以画几条?
1.放
2.靠
3.画线
l
如图,已知直线 l,作l的垂线.
工具:直尺、三角板
无数条
4.垂线的画法
O
A
l
A
如图,已知直线 l 和l外的一点A,过点A作l的垂线.
B
则所画直线AB是过点A的直线l的垂线.
0
1
2
3
4
5
6
7
8
9
10
11
Cm
4.垂线的画法
通过画图我们可以知道经过一点(已知直线上或直线外),
能画出已知直线的一条垂线,并且只能画出一条垂线.
即:在同一平面内,过一点有且只有一条直线与已知直线垂直.
“一落”即让三角形的一条直角边落在已知直线上;
“二移”即沿直线移动三角尺,使其另一直角边经过已知点;
“三画”即沿此直线边画直线,则这条直线就是已知直线的垂线.
垂线的画法
垂线的性质
例 如图,直线AB,CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.
解:因为 AB⊥OE (已知),
所以∠EOB=90°(垂直的定义).
因为 ∠BOD =∠1=55° (对顶角相等),
所以 ∠EOD =∠EOB +∠BOD
=90°+55°
=145°.
A
C
E
B
D
O
1
灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短?
我们可以将这条河看成一条直线l,从而将这个实际问题转化成数学问题.
l
简单说成:垂线段最短.
由直线外一点向直线引垂线,这点与垂足间的线段叫做垂线段.
P
l
A
5.垂线段
连接直线外一点与直线上各点的所有线段中,垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
P
l
A
6.点到直线的距离
2.如图,CD⊥AB, ∠ACB=90° ,线段AC,BC,CD中最短的是( )
A.AC B.CD C.BC D.不能确定
B
D
A
B
C
1.已知点A,与点A的距离是5cm的直线可画( )
A. 1条 B. 2条 C. 3条 D. 无数条
D
3.如图,过点P分别作OA,OB的垂线.
O
A
B
P
M
N
注意:过一点作已知线段(或射线)的垂线,
就是作这条线段(或射线)所在直线的垂线.
4.如图,直线AB,CD交于点O,EO⊥AB,垂足为O,∠EOC=35°,则∠AOD是多少度?
解:因为EO⊥AB,
所以∠BOE=90°.
又因为∠COE=35°,
所以∠COB=∠COE+∠BOE=125°.
因为∠AOD=∠COB(对顶角相等),
所以∠AOD=125°.
1.垂线:在同一平面内,过一点有且只有一条直线与已知直线垂直.
2.垂线段:连接直线外一点与直线上各点的所有线段中,垂线段最短.
3.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
