5.2.2 平行线的判定 课件 (共11张PPT)
文档属性
| 名称 | 5.2.2 平行线的判定 课件 (共11张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 00:00:00 | ||
图片预览



文档简介
(共11张PPT)
第五章 相交线与平行线
5.2.2 平行线的判定
是否平行?
我们知道,在同一平面内,不相交的两条直线平行,那么如何判定两条直线是否平行呢?
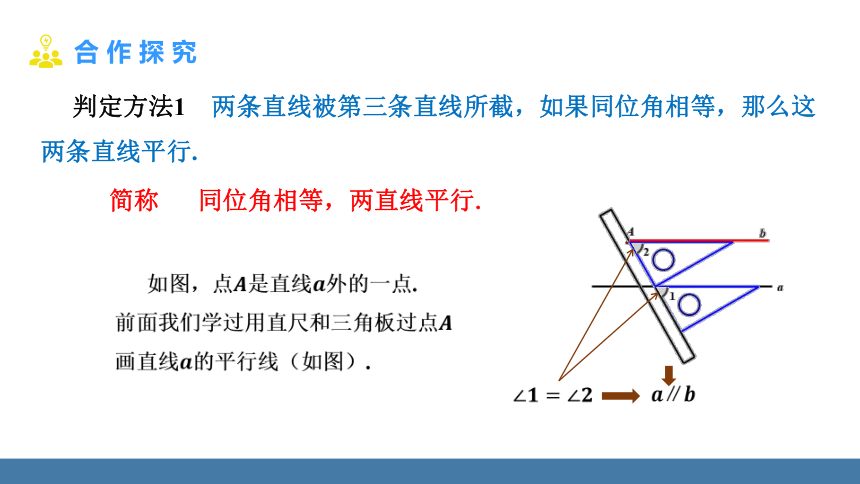
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
如图,点是直线外的一点.
前面我们学过用直尺和三角板过点
画直线的平行线(如图).
∥
简称 同位角相等,两直线平行.
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称 内错角相等,两直线平行.
如图,直线与直线相交,,那么是否平行呢?
所以∥(同位角相等,两直线平行)
因为,(已知)
,(对顶角相等)
所以,(等量代换)
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称 同旁内角互补,两直线平行.
∴∥(内错角相等,两直线平行).
∵,
,
∴,
如图,直线与直线相交,,
那么是否平行呢?
用符号“∵”表示“因为”,
符号“∴”表示“所以”.
平行线的判定方法归纳
3. 内错角相等,两直线平行.
4. 同旁内角互补,两直线平行.
2. 同位角相等,两直线平行.
1. 如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
如图,若,那么直线与平行吗?为什么?
解:
直线与平行.
理由如下:
∵,
,
∴.
∵,
∴.
∴∥(同位角相等,两直线平行).
1.如图,点E在AC的延长线上,下列条件中能判断BD∥AE的是( )
A. ∠1=∠2 B. ∠2=∠3
C. ∠A=∠DCE D. ∠3=∠4
D
2.如图,下列条件不能判断直线a∥b的是( )
A. ∠1=∠4 B. ∠3=∠5
C. ∠2+∠5=180° D. ∠2+∠4=180°
D
3.如图,已知∠1=∠2,∠3+∠4=180°,说明:AB∥EF.
解: ∵∠1=∠2,∴AB∥CD.
∵∠3+∠4=180°,∴CD∥EF,
∴AB∥EF.
平行线的判定方法
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
第五章 相交线与平行线
5.2.2 平行线的判定
是否平行?
我们知道,在同一平面内,不相交的两条直线平行,那么如何判定两条直线是否平行呢?
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
如图,点是直线外的一点.
前面我们学过用直尺和三角板过点
画直线的平行线(如图).
∥
简称 同位角相等,两直线平行.
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称 内错角相等,两直线平行.
如图,直线与直线相交,,那么是否平行呢?
所以∥(同位角相等,两直线平行)
因为,(已知)
,(对顶角相等)
所以,(等量代换)
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称 同旁内角互补,两直线平行.
∴∥(内错角相等,两直线平行).
∵,
,
∴,
如图,直线与直线相交,,
那么是否平行呢?
用符号“∵”表示“因为”,
符号“∴”表示“所以”.
平行线的判定方法归纳
3. 内错角相等,两直线平行.
4. 同旁内角互补,两直线平行.
2. 同位角相等,两直线平行.
1. 如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
如图,若,那么直线与平行吗?为什么?
解:
直线与平行.
理由如下:
∵,
,
∴.
∵,
∴.
∴∥(同位角相等,两直线平行).
1.如图,点E在AC的延长线上,下列条件中能判断BD∥AE的是( )
A. ∠1=∠2 B. ∠2=∠3
C. ∠A=∠DCE D. ∠3=∠4
D
2.如图,下列条件不能判断直线a∥b的是( )
A. ∠1=∠4 B. ∠3=∠5
C. ∠2+∠5=180° D. ∠2+∠4=180°
D
3.如图,已知∠1=∠2,∠3+∠4=180°,说明:AB∥EF.
解: ∵∠1=∠2,∴AB∥CD.
∵∠3+∠4=180°,∴CD∥EF,
∴AB∥EF.
平行线的判定方法
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
