5.3.2 命题、定理、证明 课件 (共14张PPT)
文档属性
| 名称 | 5.3.2 命题、定理、证明 课件 (共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第五章 相交线与平行线
5.3.2 命题、定理、证明
命题、定理、证明
对某一事件进行研究,必然要对这一事件进行相应的判断,并对这些判断说明理由,这就要涉及到命题和证明的知识.
1. 命题的定义:
判断一件事情的语句,叫做命题.
看下面对“角”和“有理数”进行判断的语句:
①如果两个角都是直角,那么这两个角相等.
②同角的余角相等.
③两个锐角之和是钝角.
④两个负数,绝对值大的反而小.
⑤负数与负数的和是负数.
上面这些语句,都是对一件事情做出判断的句子,它们都叫命题.
2. 命题的组成:
如果两个角都是直角,那么这两个角相等.
两个负数,绝对值大的反而小.
由已知推出的事项.
命题
已知事项.
已知事项
题设
结论
由已知推出的事项
已知事项
题设
结论
由已知推出的事项
看下面两个命题
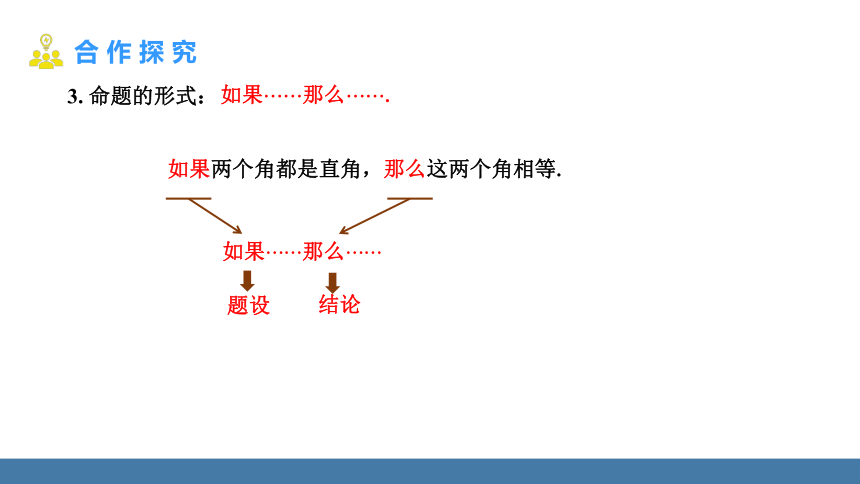
3. 命题的形式:
如果两个角都是直角,那么这两个角相等.
如果那么.
如果那么
题设
结论
4. 命题的分类:
两个锐角之和是钝角
同角的余角相等
正确的命题
真命题
错误的命题
假命题
题设成立,结论一定成立的命题叫做真命题.
题设成立,结论不一定成立的命题叫做假命题.
5. 定理:
如,“内错角相等,两条直线平行” ,是平行线的判定定理.
可以作为判定其他命题真假依据的真命题叫做定理.
6. 基本事实(公理):
经过实践检验,被公认的真命题叫做基本事实.
如“两点之间,线段最短”,“经过直线外一点,有且只有一条直线与已知直线垂直”都是基本事实.
判断一个真命题正确性的推理过程叫做证明.
7. 证明:
证明:对顶角相等.
已知:直线相交于点
求证:∠∠
证明:∵∠∠(补角的定义).
∠∠(补角的定义).
∴∠∠(同角的补角相等).
说明一个命题是假命题的方法:举出一个反例,这个反例符合命题的题设,
但不能满足结论.
说明“两个锐角之和是钝角”是假命题.
∵∠∠
设∠∠,
则∠∠都是锐角.
∴∠∠是锐角.
∴两个锐角之和是钝角是假命题.
1.下列四个句子中是命题的是______________(填序号).
①延长线段AB.②对顶角相等.③同旁内角不互补,两条直线就不平行.④在同一平面内,不相交的两条直线叫做平行线.
②③④
分析: ①陈述句,不是判断句,所以不是命题.
②③④都是判断句,所以都是命题.
2.下列命题是真命题的是___________________(填序号).
①对顶角相等.②直角都相等.③相等的角是对顶角.
④若,那么.
⑤若,则.
①②⑤
1.“对顶角相等”是_______ 命题(真、假),写成“如果…,那么…”的形式为___________________________________________ .
如果两个角是对顶角,那么两个角相等
真
2.下列语句中,是命题的是( )
A. 直线AB和CD垂直吗
B. 过线段AB的中点C画AB的垂线
C. 同旁内角不互补,两直线不平行
D. 连接A,B两点
C
3.对假命题“任何一个角的补角都不小于这个角”举一个反例并画出图形,说明其是假命题.
解:如图,∠,∠, ∠是∠的补角,而∠∠.
所以,“任何一个角的补角都不小于这个角”是假命题.
判断一件事情的语句,叫做命题.命题由题设和结论组成.
数学中的命题通常写成“如果那么 ”的形式.
可以作为判定其他命题真假的依据的真命题叫做定理.
判断一个真命题正确性的推理过程叫做证明.
说明一个命题是假命题只要举出一个反例.
第五章 相交线与平行线
5.3.2 命题、定理、证明
命题、定理、证明
对某一事件进行研究,必然要对这一事件进行相应的判断,并对这些判断说明理由,这就要涉及到命题和证明的知识.
1. 命题的定义:
判断一件事情的语句,叫做命题.
看下面对“角”和“有理数”进行判断的语句:
①如果两个角都是直角,那么这两个角相等.
②同角的余角相等.
③两个锐角之和是钝角.
④两个负数,绝对值大的反而小.
⑤负数与负数的和是负数.
上面这些语句,都是对一件事情做出判断的句子,它们都叫命题.
2. 命题的组成:
如果两个角都是直角,那么这两个角相等.
两个负数,绝对值大的反而小.
由已知推出的事项.
命题
已知事项.
已知事项
题设
结论
由已知推出的事项
已知事项
题设
结论
由已知推出的事项
看下面两个命题
3. 命题的形式:
如果两个角都是直角,那么这两个角相等.
如果那么.
如果那么
题设
结论
4. 命题的分类:
两个锐角之和是钝角
同角的余角相等
正确的命题
真命题
错误的命题
假命题
题设成立,结论一定成立的命题叫做真命题.
题设成立,结论不一定成立的命题叫做假命题.
5. 定理:
如,“内错角相等,两条直线平行” ,是平行线的判定定理.
可以作为判定其他命题真假依据的真命题叫做定理.
6. 基本事实(公理):
经过实践检验,被公认的真命题叫做基本事实.
如“两点之间,线段最短”,“经过直线外一点,有且只有一条直线与已知直线垂直”都是基本事实.
判断一个真命题正确性的推理过程叫做证明.
7. 证明:
证明:对顶角相等.
已知:直线相交于点
求证:∠∠
证明:∵∠∠(补角的定义).
∠∠(补角的定义).
∴∠∠(同角的补角相等).
说明一个命题是假命题的方法:举出一个反例,这个反例符合命题的题设,
但不能满足结论.
说明“两个锐角之和是钝角”是假命题.
∵∠∠
设∠∠,
则∠∠都是锐角.
∴∠∠是锐角.
∴两个锐角之和是钝角是假命题.
1.下列四个句子中是命题的是______________(填序号).
①延长线段AB.②对顶角相等.③同旁内角不互补,两条直线就不平行.④在同一平面内,不相交的两条直线叫做平行线.
②③④
分析: ①陈述句,不是判断句,所以不是命题.
②③④都是判断句,所以都是命题.
2.下列命题是真命题的是___________________(填序号).
①对顶角相等.②直角都相等.③相等的角是对顶角.
④若,那么.
⑤若,则.
①②⑤
1.“对顶角相等”是_______ 命题(真、假),写成“如果…,那么…”的形式为___________________________________________ .
如果两个角是对顶角,那么两个角相等
真
2.下列语句中,是命题的是( )
A. 直线AB和CD垂直吗
B. 过线段AB的中点C画AB的垂线
C. 同旁内角不互补,两直线不平行
D. 连接A,B两点
C
3.对假命题“任何一个角的补角都不小于这个角”举一个反例并画出图形,说明其是假命题.
解:如图,∠,∠, ∠是∠的补角,而∠∠.
所以,“任何一个角的补角都不小于这个角”是假命题.
判断一件事情的语句,叫做命题.命题由题设和结论组成.
数学中的命题通常写成“如果那么 ”的形式.
可以作为判定其他命题真假的依据的真命题叫做定理.
判断一个真命题正确性的推理过程叫做证明.
说明一个命题是假命题只要举出一个反例.
