6.1.1 算术平方根(1) 课件 (共17张PPT)
文档属性
| 名称 | 6.1.1 算术平方根(1) 课件 (共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第六章 实数
6.1.1 算术平方根(1)
1.了解算术平方根的概念,会用根号表示正数的算术平方根,并了解算术平方根的非负性;
2.了解开方与乘方互为逆运算,会求某些非负数的算术平方根;
学校要举行美术作品比赛,小明很高兴,他想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?你能帮小明算一算吗?
5 dm
因为 52=25
正方形的边长/dm 1 3 4 6
正方形的面积/dm2
1
9
16
36
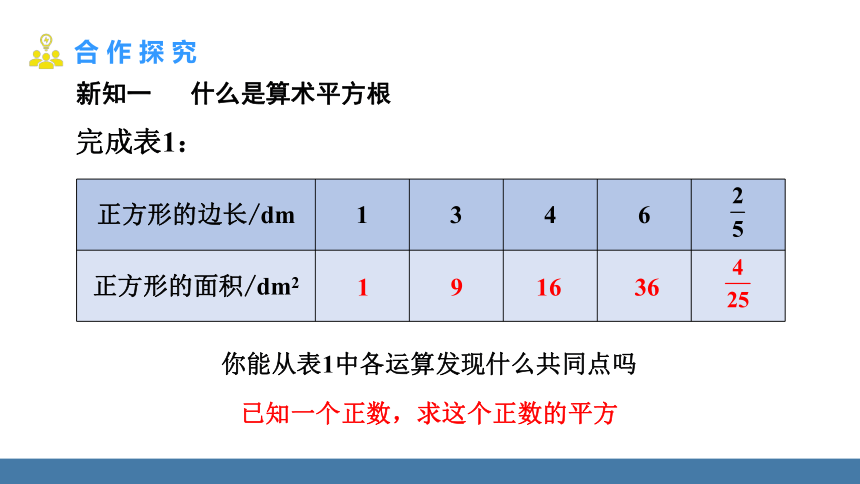
完成表1:
你能从表1中各运算发现什么共同点吗
已知一个正数,求这个正数的平方
新知一 什么是算术平方根
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
1
3
4
6
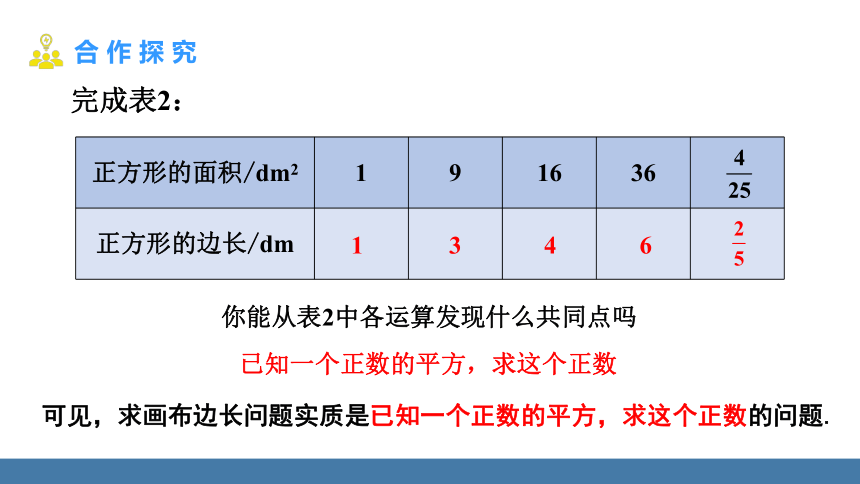
完成表2:
你能从表2中各运算发现什么共同点吗
已知一个正数的平方,求这个正数
可见,求画布边长问题实质是已知一个正数的平方,求这个正数的问题.
一般地,如果一个正数 x 的平方等于 a ,即 x a,那么这个正数 x 叫做 a 的算术平方根.
规定:0的算术平方根是0.
算术平方根是它本身的数只有0和1.
1.因为2 4,所以4的算术平方根是_____;
2
2.下列说法正确的是______.
①
①5是25的算术平方根.
②0.01是0.1的算术平方根.
x =a (x≥0)
x =
a的算术平方根
读作:根号a
互为
逆运算
被开方数
(a≥0)
新知二 算术平方根的符号表示
平方根号
例1 下列各式是否有意义?为什么?
有
有
有
无
(1)定义:一般地,如果一个正数的平方等于a,即x2=a,那么这个
正数x叫做a的 .
算术平方根
(2)表示方法:a的算术平方根记为 ,读作“根号a”,a叫做
被开方数.
(3)温馨提示:
①规定0的算术平方根是 ;
算术平方根是本身的数有 和 ;
②正数有 个算术平方根,负数 算术平方根;
没有
1
1
0
0
③算术平方根具有双重非负性:a≥0及≥0.
求下列各数的算术平方根:
(1)100; (2) ; (3)0.0001.
102=100
100的算术平方根是10
的算术平方根是
0.012=0.0001
0.0001的算术平方根是0.01
(1)
(2)
(3)
被开方数越大,对应的算术平方根也越大
新知三 求算术平方根
例4 下列说法正确的是 .
①4是25的算术平方根.
② 0.01是0.1的算术平方根.
①
例2 下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
例3 16的算术平方根是 .
4
1.数4的算术平方根是( )
A.2 B.-2 C.±2 D.
A
A
3.填空:
(1) 一个数的算术平方根是8,则这个数是 .
(2) 一个自然数的算术平方根为a,则这个自然数是 ;和这个
自然数相邻的下一个自然数是 .
4.计算:
(1) 的算术平方根为 .
2的算术平方根为 .
(3)的结果是 .
3
64
a2
a2+1
3
5.求下列各数的算术平方根:
(1)121; (2) ; (3) 0.000004.
解:(1)因为112 =121,所以121的算术平方根是11,即 ;
(2)因为 ,所以 的算术平方根是 ,
即
(3)因为0.0022 =0.000004,所以0.000004的算术平方根
是0.002,即
解:设每块地板砖的边长为x m.由题意得
6.用大小完全相同的240块正方形地板砖,铺一间面积为60 m2的会
议室的地面,每块地板砖的边长是多少?
故每块地板砖的边长是0.5 m.
7.已知: .
求x-3y+4z的值.
解:由题意得:
解得
如果一个正数x的平方等于a,即x a,那么这个正数x叫做a的算术平方根,a的算术平方根记为,读作“根号a”,a叫做被开方数.
算术
平方根
的双重非负性:
应用:
几个非负数的和为0,则每个数均为0.
概念:
即
第六章 实数
6.1.1 算术平方根(1)
1.了解算术平方根的概念,会用根号表示正数的算术平方根,并了解算术平方根的非负性;
2.了解开方与乘方互为逆运算,会求某些非负数的算术平方根;
学校要举行美术作品比赛,小明很高兴,他想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?你能帮小明算一算吗?
5 dm
因为 52=25
正方形的边长/dm 1 3 4 6
正方形的面积/dm2
1
9
16
36
完成表1:
你能从表1中各运算发现什么共同点吗
已知一个正数,求这个正数的平方
新知一 什么是算术平方根
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
1
3
4
6
完成表2:
你能从表2中各运算发现什么共同点吗
已知一个正数的平方,求这个正数
可见,求画布边长问题实质是已知一个正数的平方,求这个正数的问题.
一般地,如果一个正数 x 的平方等于 a ,即 x a,那么这个正数 x 叫做 a 的算术平方根.
规定:0的算术平方根是0.
算术平方根是它本身的数只有0和1.
1.因为2 4,所以4的算术平方根是_____;
2
2.下列说法正确的是______.
①
①5是25的算术平方根.
②0.01是0.1的算术平方根.
x =a (x≥0)
x =
a的算术平方根
读作:根号a
互为
逆运算
被开方数
(a≥0)
新知二 算术平方根的符号表示
平方根号
例1 下列各式是否有意义?为什么?
有
有
有
无
(1)定义:一般地,如果一个正数的平方等于a,即x2=a,那么这个
正数x叫做a的 .
算术平方根
(2)表示方法:a的算术平方根记为 ,读作“根号a”,a叫做
被开方数.
(3)温馨提示:
①规定0的算术平方根是 ;
算术平方根是本身的数有 和 ;
②正数有 个算术平方根,负数 算术平方根;
没有
1
1
0
0
③算术平方根具有双重非负性:a≥0及≥0.
求下列各数的算术平方根:
(1)100; (2) ; (3)0.0001.
102=100
100的算术平方根是10
的算术平方根是
0.012=0.0001
0.0001的算术平方根是0.01
(1)
(2)
(3)
被开方数越大,对应的算术平方根也越大
新知三 求算术平方根
例4 下列说法正确的是 .
①4是25的算术平方根.
② 0.01是0.1的算术平方根.
①
例2 下列说法正确的是( )
A.因为62=36,所以6是36的算术平方根
B.因为(-6)2=36,所以-6是36的算术平方根
C.因为(±6)2=36,所以6和-6都是36的算术平方根
D.以上说法都不对
A
例3 16的算术平方根是 .
4
1.数4的算术平方根是( )
A.2 B.-2 C.±2 D.
A
A
3.填空:
(1) 一个数的算术平方根是8,则这个数是 .
(2) 一个自然数的算术平方根为a,则这个自然数是 ;和这个
自然数相邻的下一个自然数是 .
4.计算:
(1) 的算术平方根为 .
2的算术平方根为 .
(3)的结果是 .
3
64
a2
a2+1
3
5.求下列各数的算术平方根:
(1)121; (2) ; (3) 0.000004.
解:(1)因为112 =121,所以121的算术平方根是11,即 ;
(2)因为 ,所以 的算术平方根是 ,
即
(3)因为0.0022 =0.000004,所以0.000004的算术平方根
是0.002,即
解:设每块地板砖的边长为x m.由题意得
6.用大小完全相同的240块正方形地板砖,铺一间面积为60 m2的会
议室的地面,每块地板砖的边长是多少?
故每块地板砖的边长是0.5 m.
7.已知: .
求x-3y+4z的值.
解:由题意得:
解得
如果一个正数x的平方等于a,即x a,那么这个正数x叫做a的算术平方根,a的算术平方根记为,读作“根号a”,a叫做被开方数.
算术
平方根
的双重非负性:
应用:
几个非负数的和为0,则每个数均为0.
概念:
即
