6.1.1 算术平方根(3) 课件 (共19张PPT)
文档属性
| 名称 | 6.1.1 算术平方根(3) 课件 (共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 11:46:29 | ||
图片预览






文档简介
(共19张PPT)
第六章 实数
6.1.1 算术平方根(3)
1.掌握平方根的概念,明确平方根和算术平方根之间的联系和区别;
2.能用符号正确地表示一个数的平方根,理解开方运算和乘方运算之间的互逆关系;
3.通过探索平方根与算术平方根的区别与联系,学会利用算术平方根解决平方根的问题;
4.通过对平方根的学习,培养学生从多方面、多角度分析解决问题的思想意识,养成全面分析问题的习惯.
2.判断下列各数有没有算术平方根?如果有,请求出它们的算术平方根.
-36 , 0.09 , , 0 , 2 , .
-36没有算术平方根.
1.什么是算术平方根?
如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做
a的算术平方根.
2的算术平方根是
如果一个数的平方等于9,这个数是多少?
答:3或 3
由于( 3) =9,那么这个数也可以是 3
填表:
x2 1 16 36 49
x
新知一 平方根的定义
一般地,如果一个数的平方等于 a,那么这个数叫做 a 的平方根或二次方根.这就是说,如果 x2=a,那么 x 叫做 a 的平方根.
例如,3 和 3 是 9 的平方根,简记为 3 是 9 的平方根.
注意:一个正数有两个平方根,不要丢掉负的平方根.
1
4
9
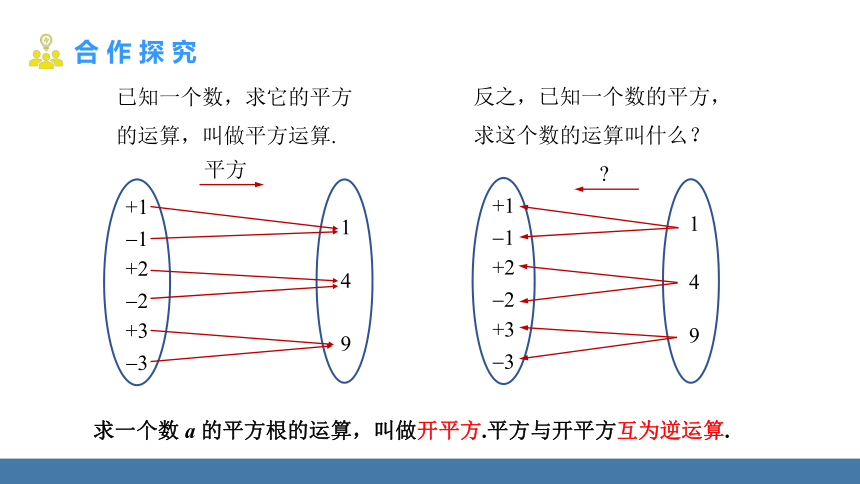
已知一个数,求它的平方的运算,叫做平方运算.
+1
1
+2
2
+3
3
平方
1
4
9
+1
1
+2
2
+3
3
反之,已知一个数的平方,求这个数的运算叫什么?
求一个数 a 的平方根的运算,叫做开平方.平方与开平方互为逆运算.
例1 求下列各数的平方根.
(1)100 (2) (3)0.25
解:(1)因为(±10)2=100,所以100的平方根是±10.
(3)因为(±0.5)2=0.25,所以0.25的平方根是±0.5.
新知二 平方根的性质
1. 144的平方根是什么?
2. 0的平方根是什么?
3.
的平方根是什么?
4. -49有没有平方根?为什么?
0
没有,因为一个数的平方不可能是负数
通过这些题目的解答,你能发现什么
问题:(1)正数有几个平方根?它们什么关系?
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
(2)0的平方根是多少?
(3)负数呢?
正数有两个平方根,它们互为相反数
0的平方根是0
(1)平方根的性质:
1.正数有两个平方根,两个平方根互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
(2)平方根的表示方法:
正数a有两个平方根,一个是a的算术平方根 ,另一个是 ,它们互为相反数.这两个平方根合起来可以记作 读作“正、负根号a”.
求下列各式的值:
(1) ; (2) ; (3) .
例2
解:(1)因为62=36,所以 =6;
(2)因为0.92=0.81,所以 ;
(3)因为 ,所以 .
例3 一个正数的两个平方根分别是2a+1和a-4,
求这个数.
解:由于一个正数的两个平方根是2a+1和a-4,
则有2a+1+a-4=0,即3a-3=0,
解得a=1.
所以这个数为(2a+1)2=(2+1)2=9.
方法归纳:一个正数有两个平方根,它们互为相反数.
1.下列说法不正确的是( )
A.0的平方根是0
B. 的平方根是2
C.正数的平方根互为相反数
D.一个正数的算术平方根一定大于这个数的相反数
B
3 .如果x2=a,那么下列说法错误的是( )
A.若x确定,则a的值是唯一的
B.若a确定,则x的值是唯一的
C.a是x的平方
D.x是a的平方根
B
C
2.(-3)2的平方根是( )
A.3 B.-3 C.±3 D.
D
5.下列说法正确的是_________
① -3是9的平方根; ②25的平方根是5;
③ -36的平方根是-6; ④平方根等于0的数是0;
⑤64的算术平方根是8.
①④⑤
4.若8xmy与6x3yn的和是单项式,则(m+n)3的平方根为( )
A.4 B.8 C.±4 D.±8
6. 判断下列说法是否正确:
正确.
(4)-42的平方根是-4.
(1) 是 的一个平方根;
(2) 是6的算术平方根;
(3) 的值是±4;
正确.
不正确,是 4.
不正确,
负数没有平方根
7. 分别求 64, ,6.25 , 的平方根.
64的平方根是8与-8,
的平方根是 与 ,
6.25的平方根是2.5与-2.5.
的平方根是3和-3.
解:
解:(1)
(2)
8.求下列各式的值:
(1)
(2)
(3)
(3)
1.包含关系:平方根包含算术平方根,算术平方
根是平方根的一种.
平方根与算术平方根的联系与区别:
2.只有非负数才有平方根和算术平方根.
3.0的平方根是0,算术平方根也是0.
区别
1.个数不同:一个正数有两个平方根,
但只有一个算术平方根.
2.表示法不同:平方根表示为 ,
而算术平方根表示为 .
联系
第六章 实数
6.1.1 算术平方根(3)
1.掌握平方根的概念,明确平方根和算术平方根之间的联系和区别;
2.能用符号正确地表示一个数的平方根,理解开方运算和乘方运算之间的互逆关系;
3.通过探索平方根与算术平方根的区别与联系,学会利用算术平方根解决平方根的问题;
4.通过对平方根的学习,培养学生从多方面、多角度分析解决问题的思想意识,养成全面分析问题的习惯.
2.判断下列各数有没有算术平方根?如果有,请求出它们的算术平方根.
-36 , 0.09 , , 0 , 2 , .
-36没有算术平方根.
1.什么是算术平方根?
如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做
a的算术平方根.
2的算术平方根是
如果一个数的平方等于9,这个数是多少?
答:3或 3
由于( 3) =9,那么这个数也可以是 3
填表:
x2 1 16 36 49
x
新知一 平方根的定义
一般地,如果一个数的平方等于 a,那么这个数叫做 a 的平方根或二次方根.这就是说,如果 x2=a,那么 x 叫做 a 的平方根.
例如,3 和 3 是 9 的平方根,简记为 3 是 9 的平方根.
注意:一个正数有两个平方根,不要丢掉负的平方根.
1
4
9
已知一个数,求它的平方的运算,叫做平方运算.
+1
1
+2
2
+3
3
平方
1
4
9
+1
1
+2
2
+3
3
反之,已知一个数的平方,求这个数的运算叫什么?
求一个数 a 的平方根的运算,叫做开平方.平方与开平方互为逆运算.
例1 求下列各数的平方根.
(1)100 (2) (3)0.25
解:(1)因为(±10)2=100,所以100的平方根是±10.
(3)因为(±0.5)2=0.25,所以0.25的平方根是±0.5.
新知二 平方根的性质
1. 144的平方根是什么?
2. 0的平方根是什么?
3.
的平方根是什么?
4. -49有没有平方根?为什么?
0
没有,因为一个数的平方不可能是负数
通过这些题目的解答,你能发现什么
问题:(1)正数有几个平方根?它们什么关系?
因为任何实数的平方都为非负数,所以负数没有平方根,也没有算术平方根.
(2)0的平方根是多少?
(3)负数呢?
正数有两个平方根,它们互为相反数
0的平方根是0
(1)平方根的性质:
1.正数有两个平方根,两个平方根互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
(2)平方根的表示方法:
正数a有两个平方根,一个是a的算术平方根 ,另一个是 ,它们互为相反数.这两个平方根合起来可以记作 读作“正、负根号a”.
求下列各式的值:
(1) ; (2) ; (3) .
例2
解:(1)因为62=36,所以 =6;
(2)因为0.92=0.81,所以 ;
(3)因为 ,所以 .
例3 一个正数的两个平方根分别是2a+1和a-4,
求这个数.
解:由于一个正数的两个平方根是2a+1和a-4,
则有2a+1+a-4=0,即3a-3=0,
解得a=1.
所以这个数为(2a+1)2=(2+1)2=9.
方法归纳:一个正数有两个平方根,它们互为相反数.
1.下列说法不正确的是( )
A.0的平方根是0
B. 的平方根是2
C.正数的平方根互为相反数
D.一个正数的算术平方根一定大于这个数的相反数
B
3 .如果x2=a,那么下列说法错误的是( )
A.若x确定,则a的值是唯一的
B.若a确定,则x的值是唯一的
C.a是x的平方
D.x是a的平方根
B
C
2.(-3)2的平方根是( )
A.3 B.-3 C.±3 D.
D
5.下列说法正确的是_________
① -3是9的平方根; ②25的平方根是5;
③ -36的平方根是-6; ④平方根等于0的数是0;
⑤64的算术平方根是8.
①④⑤
4.若8xmy与6x3yn的和是单项式,则(m+n)3的平方根为( )
A.4 B.8 C.±4 D.±8
6. 判断下列说法是否正确:
正确.
(4)-42的平方根是-4.
(1) 是 的一个平方根;
(2) 是6的算术平方根;
(3) 的值是±4;
正确.
不正确,是 4.
不正确,
负数没有平方根
7. 分别求 64, ,6.25 , 的平方根.
64的平方根是8与-8,
的平方根是 与 ,
6.25的平方根是2.5与-2.5.
的平方根是3和-3.
解:
解:(1)
(2)
8.求下列各式的值:
(1)
(2)
(3)
(3)
1.包含关系:平方根包含算术平方根,算术平方
根是平方根的一种.
平方根与算术平方根的联系与区别:
2.只有非负数才有平方根和算术平方根.
3.0的平方根是0,算术平方根也是0.
区别
1.个数不同:一个正数有两个平方根,
但只有一个算术平方根.
2.表示法不同:平方根表示为 ,
而算术平方根表示为 .
联系
