6.2 立方根 课件 (共23张PPT)
文档属性
| 名称 | 6.2 立方根 课件 (共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第六章 实数
6.2 立方根
1.(课标)了解立方根的概念,会用根号表示数的立方根.
2.(课标)了解乘方与开方互为逆运算,会用立方运算求百以内整数的立方根.
3.会利用立方根的概念解简单的方程.
4.(课标)会用计算器求立方根.
某化工厂使用半径为1米的一种球形储气罐储藏气体,现在要造一个新的球形储气罐,如果要求它的体积必须是原来体积的8倍,那么它的半径应是原来储气罐半径的多少倍?
要做一个体积为27cm3的正方体模型(如图),它的棱长要取多少?你是怎么知道的?
思考:如果问题中正方体的体积为5cm3,正方体
的棱长又该是多少?
设正方体的棱长为 x ㎝,则
这就是要求一个数,使它的立方等于27.
因为
所以 x=3. 正方体的棱长为3㎝
立方根的概念
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.记作 .
立方根的表示
一个数a的立方根可以表示为:
根指数
被开方数
其中a是被开方数,3是根指数,3不能省略.
读作:三次根号 a,
填一填: 根据立方根的意义填空:
因为 =8,所以8的立方根是( );
因为( )3 =0.064,所以0.064的立方是( );
因为( )3 =0,所以0的立方根是( );
因为 ( )3 =-8,所以-8的立方根是( );
因为( )3 = ,所以 的立方根是( ).
0
2
-2
0
-2
0.4
0.4
通过上述计算,你能发现正数、0和负数的立方根各有什么特点吗?
立方根的性质
正数的立方根是正数,
负数的立方根是负数,
零的立方根是零.
立方根是它本身的数有
1, -1, 0;平方根是它本身的数只有0.
例1 如果一个数的立方根与其算术平方根相同,那么这个
数是( )
A.1 B.0或1
C.0或±1 D.任意非负数
B
解析:因为算术平方根必为非负数,而一个数的立方根与其本身符号相同,所以此数必为0或正数;
对除1以外的任意正数n,恒有n3>n2. 故选B.
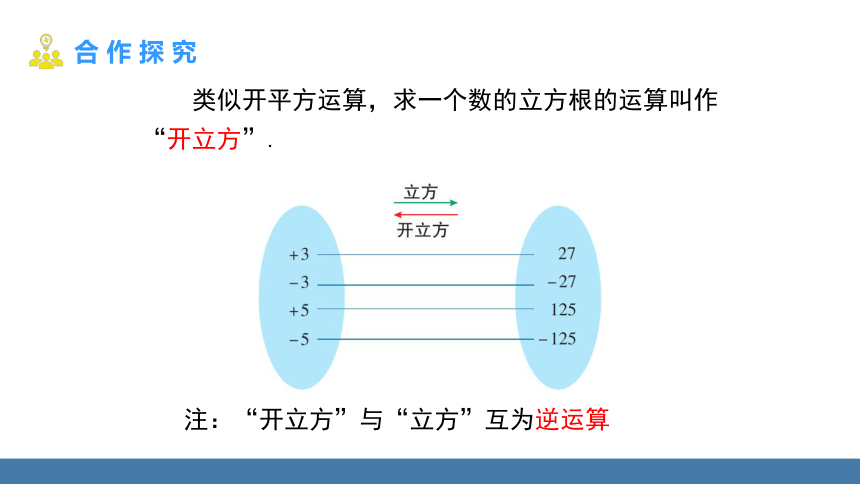
类似开平方运算,求一个数的立方根的运算叫作“开立方”.
注:“开立方”与“立方”互为逆运算
因为 =____, =____,
所以 ____ ;
因为 =____, =____,
所以 ____ ;
– 2
– 2
=
– 3
– 3
一般地,
=
=
你能归纳出立方根的另一性质吗?
平方根 立方根
性 质 正数
0
负数
表示方法
被开方数的范围
两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
平方根与立方根的区别和联系
可以为任何数
非负数
例2 已知x-2的平方根是±2,2x+y+7的立方根是3,
求x2+y2的算术平方根.
分析:根据平方根、立方根的定义和已知条件可知x-2=4,
2x+y+7=27,从而解出x,y,最后代入x2+y2求其
算术平方根即可.
∵x-2的平方根是±2, ∴x-2=4. ∴x=6.
∵2x+y+7的立方根是3, ∴2x+y+7=27.
把x=6代入得:y=8,
∴x2+y2=62+82=100.
∴x2+y2的算术平方根为10.
解:
例3 用计算器求下列各数的立方根:343,-1.331.
解:依次按键:
显示:7
所以,
2ndF
4
3
3
=
依次按键:
显示:-1.1
所以,
1
2ndF
-
.
3
1
3
=
由于一个数的立方根可能是无限不循环小数,所以我们可以利用计算器求一个数的立方根或它的近似值.
不同的计算器的按键方式可能有所差别!
用计算器求立方根
用计算器计算 , , , ,…,你能发现什么规律?
= 6
= 0.6
= 0.06
= 60
小结:被开方数的小数点向左或向右移动3n位时立方根的小数点就相应的向左或向右移动n位(n为正整数).
例4 用计算器计算 (精确到0.001),并利用你发现的规律求 , , 的近似值.
解:依次按键:
显示:4.641588834,精确到0.001为4.642
所以,
2ndF
0
1
0
=
所以 , , .
B
A
D
4.若x2=(-5)2, =-5,则x+y的值为( )
A.0 B.-10
C.0或-10 D.0或-10或10
C
C
0.5
-3
10
1
100
8.比较3,4, 的大小.
解:33 = 27,43 = 64
因为27 < 50 < 64
所以3 < < 4
9.立方根概念的起源与几何中的正方体有关,如果一个正方体的体积为V,那么这个正方体的棱长为多少?
解:
10.比较下列各组数的大小.
(1) 与2.5; (2) 与 .
解:因为 = 9
2.53 = 15.625
所以 < 15.625
所以 < 2.5
因为 = 3
所以 3 <
所以 <
第六章 实数
6.2 立方根
1.(课标)了解立方根的概念,会用根号表示数的立方根.
2.(课标)了解乘方与开方互为逆运算,会用立方运算求百以内整数的立方根.
3.会利用立方根的概念解简单的方程.
4.(课标)会用计算器求立方根.
某化工厂使用半径为1米的一种球形储气罐储藏气体,现在要造一个新的球形储气罐,如果要求它的体积必须是原来体积的8倍,那么它的半径应是原来储气罐半径的多少倍?
要做一个体积为27cm3的正方体模型(如图),它的棱长要取多少?你是怎么知道的?
思考:如果问题中正方体的体积为5cm3,正方体
的棱长又该是多少?
设正方体的棱长为 x ㎝,则
这就是要求一个数,使它的立方等于27.
因为
所以 x=3. 正方体的棱长为3㎝
立方根的概念
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.记作 .
立方根的表示
一个数a的立方根可以表示为:
根指数
被开方数
其中a是被开方数,3是根指数,3不能省略.
读作:三次根号 a,
填一填: 根据立方根的意义填空:
因为 =8,所以8的立方根是( );
因为( )3 =0.064,所以0.064的立方是( );
因为( )3 =0,所以0的立方根是( );
因为 ( )3 =-8,所以-8的立方根是( );
因为( )3 = ,所以 的立方根是( ).
0
2
-2
0
-2
0.4
0.4
通过上述计算,你能发现正数、0和负数的立方根各有什么特点吗?
立方根的性质
正数的立方根是正数,
负数的立方根是负数,
零的立方根是零.
立方根是它本身的数有
1, -1, 0;平方根是它本身的数只有0.
例1 如果一个数的立方根与其算术平方根相同,那么这个
数是( )
A.1 B.0或1
C.0或±1 D.任意非负数
B
解析:因为算术平方根必为非负数,而一个数的立方根与其本身符号相同,所以此数必为0或正数;
对除1以外的任意正数n,恒有n3>n2. 故选B.
类似开平方运算,求一个数的立方根的运算叫作“开立方”.
注:“开立方”与“立方”互为逆运算
因为 =____, =____,
所以 ____ ;
因为 =____, =____,
所以 ____ ;
– 2
– 2
=
– 3
– 3
一般地,
=
=
你能归纳出立方根的另一性质吗?
平方根 立方根
性 质 正数
0
负数
表示方法
被开方数的范围
两个,互为相反数
一个,为正数
0
0
没有平方根
一个,为负数
平方根与立方根的区别和联系
可以为任何数
非负数
例2 已知x-2的平方根是±2,2x+y+7的立方根是3,
求x2+y2的算术平方根.
分析:根据平方根、立方根的定义和已知条件可知x-2=4,
2x+y+7=27,从而解出x,y,最后代入x2+y2求其
算术平方根即可.
∵x-2的平方根是±2, ∴x-2=4. ∴x=6.
∵2x+y+7的立方根是3, ∴2x+y+7=27.
把x=6代入得:y=8,
∴x2+y2=62+82=100.
∴x2+y2的算术平方根为10.
解:
例3 用计算器求下列各数的立方根:343,-1.331.
解:依次按键:
显示:7
所以,
2ndF
4
3
3
=
依次按键:
显示:-1.1
所以,
1
2ndF
-
.
3
1
3
=
由于一个数的立方根可能是无限不循环小数,所以我们可以利用计算器求一个数的立方根或它的近似值.
不同的计算器的按键方式可能有所差别!
用计算器求立方根
用计算器计算 , , , ,…,你能发现什么规律?
= 6
= 0.6
= 0.06
= 60
小结:被开方数的小数点向左或向右移动3n位时立方根的小数点就相应的向左或向右移动n位(n为正整数).
例4 用计算器计算 (精确到0.001),并利用你发现的规律求 , , 的近似值.
解:依次按键:
显示:4.641588834,精确到0.001为4.642
所以,
2ndF
0
1
0
=
所以 , , .
B
A
D
4.若x2=(-5)2, =-5,则x+y的值为( )
A.0 B.-10
C.0或-10 D.0或-10或10
C
C
0.5
-3
10
1
100
8.比较3,4, 的大小.
解:33 = 27,43 = 64
因为27 < 50 < 64
所以3 < < 4
9.立方根概念的起源与几何中的正方体有关,如果一个正方体的体积为V,那么这个正方体的棱长为多少?
解:
10.比较下列各组数的大小.
(1) 与2.5; (2) 与 .
解:因为 = 9
2.53 = 15.625
所以 < 15.625
所以 < 2.5
因为 = 3
所以 3 <
所以 <
