8.1 二元一次方程组 课件 (共23张PPT)
文档属性
| 名称 | 8.1 二元一次方程组 课件 (共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 12:03:19 | ||
图片预览








文档简介
(共23张PPT)
第八章 二元一次方程组
你能分出
胜负吗?
在上面的问题中,要求的是两个未知数,如果用一元一次方程来解决,列方程时,要用一个未知数表示另一个未知数.能不能根据题意直接设两个未知数,使列方程变得容易呢?我们从这个想法出发开始本章的学习.
篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分.某队在 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
8.1 二元一次方程组
1.了解二元一次方程(组)及其解的定义.
2.会检验一对数值是不是某个二元一次方程组的解.
3.能根据简单的实际问题列出二元一次方程组.
问题1 什么是方程?
含有未知数的等式叫方程.
问题2 什么是一元一次方程?
只含有一个未知数(元),未知数的次数都是 1 ,且等号两边都是等式,这样的方程叫做一元一次方程.
新知一 二元一次方程(组)
篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分.某队在 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
解:设胜 x 场,则负(10-x)场.
2x +(10-x)= 16.
问题1 如何列一元一次方程?
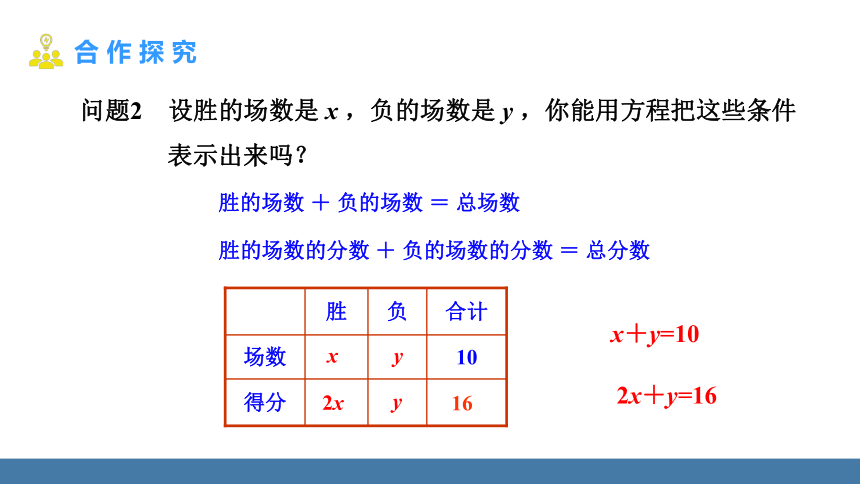
问题2 设胜的场数是 x ,负的场数是 y ,你能用方程把这些条件
表示出来吗?
胜的场数 + 负的场数 = 总场数
胜的场数的分数 + 负的场数的分数 = 总分数
得分
10
场数
合计
负
胜
x
y
2x
y
16
2x+y=16
x+y=10
思考一:上述方程有什么特点
思考二:它与一元一次方程有什么不同
x+y=10
2x+y=16
含有两个未知数,并且含有未知数的项的次数都是 1 ,像这样的方程叫作二元一次方程.
注意:二元一次方程满足的三个条件:
(1)在方程中“元”是指未知数,“二元”就是指方程中有且只有两个未知数.
(2)“未知数的次数为 1 ”是指含有未知数的项(单项式)的次数是 1.
(3)二元一次方程的左边和右边都必须是整式.
方程组中有两个未知数,含有每个未知数的项的次数都是 1,并且一共有两个方程,像这样的方程组叫作二元一次方程组.
x+y=10,
2x+y=16
叫作方程组
小提示: 也是二元一次方程组.
例1 已知下列方程,其中是二元一次方程的有______________.
【解析】只有(1)(4)(5)(8)(10)满足二元一次方程的概念.
(2)为一元一次方程,方程中只含有一个未知数;
(3)中含未知数的项的次数为 2;(6)只含有一个未知数;
(7)不是整式方程;(9)中未知数 x 的次数为 2.
(1)(4)(5)(8)(10)
【解析】A 中未知数的项的次数为 2,故 A 不是二元一次方程组;
B 中含有三个未知数,故 B 不是二元一次方程组;
C 是二元一次方程组,故 C 是二元一次方程组;
D 不是整式方程,故 D 不是二元一次方程组.
例2 下列方程组是二元一次方程组的是( )
C
A. B. C. D.
x
y
探究 满足篮球联赛问题中的方程 x + y = 10 ,且符合问题
的实际意义的值有哪些?把它们填入表中.
x 0 1 2 3 4 5 6 7 8 9 10
y 10 9 8 7 6 5 4 3 2 1 0
新知二 二元一次方程组的解
思考二:上表中哪对 x,y 的值还满足方程 2x+y=16 ②?
x=6,y=4 还满足方程②.也就是说, 它是方程 x+y=10 ①
与方程②的公共解,记作
思考一:如果不考虑方程表示的实际意义,还可以取哪些值?这些值是有限的吗?
x,y 还可取到小数,如 x=0.5,y=9.5;有无数组这样的值.
一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
例3 下列数组中,是二元一次方程 x+y=7 的解的是( )
A.
C.
D.
B.
x=-2,
y=5
x=3,
y=4
x=-1,
y=7
x=-2,
y=-5
【思路点拨】二元一次方程 x+y=7 的解有无数个,
所以此题应该用排除法确定答案,分别代入方程组,使方程左右相等的解才是方程组的解.
B
例4 判断下列各组数是否是二元一次方程组 的解.
【总结升华】检验是否是方程组的解,应把数值代入两个方程,若两个方程同时成立,才是方程组的解;而方程组中某一个方程的某一组解不一定是方程组的解.
4x+2y=2, ①
x+2y=-1. ②
x=3,
y=-5
x=1,
y=-1
(1) (2)
√
例5 加工某种产品须经两道工序,第一道工序每人每天可完成 900 件,第二道工序每人每天可完成 1 200 件. 现有 7 位工人参加这两道工序,应怎样安排人力,才能使每天第一、二道工序所完成的件数相等?请列出符合题意的二元一次方程组.
解:设安排第一道工序为 x 人,第二道工序为 y 人.
根据题意得
1.关于 x,y 的方程 ax2+bx+2y=3 是一个二元一次方程,则 a,b 的值
分别为( )
A .a=0 且 b=0 B.a=0 或 b=0 C. a=0 且 b≠0 D.a≠0 且 b≠0
2.下列不是二元一次方程组的是( )
A.
x+y=3,
x-y=1
x+ =1,
y+x=2
B.
D.
6x+4y=9,
y=3x+4
C.
x=1,
y=1
B
C
3.二元一次方程组 的解是( )
A. B. C. D.
B
4.若方程 的一个解是 ,则 a=____ .
3
5.根据下列语句,分别设适当的未知数,列出二元一次方程或方程组.
(1)摩托车的时速是货车的 2 倍,它们的速度之和是 200 km/h;
(2)某种时装的价格是某种皮装价格的 1.4 倍,5 件皮装比 3 件时装贵 700 元.
x=2y,
x+y=200.
设摩托车的速度为 x km/h,货车的速度为 y km/h,则
设时装的价格为 x 元/件,皮装的价格为 y 元/件,则
x=1.4y,
5y=3x+700.
认识二元一次方程组
二元一次方程(组)的定义
二元一次方程(组)的解
列二元一次方程组
第八章 二元一次方程组
你能分出
胜负吗?
在上面的问题中,要求的是两个未知数,如果用一元一次方程来解决,列方程时,要用一个未知数表示另一个未知数.能不能根据题意直接设两个未知数,使列方程变得容易呢?我们从这个想法出发开始本章的学习.
篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分.某队在 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
8.1 二元一次方程组
1.了解二元一次方程(组)及其解的定义.
2.会检验一对数值是不是某个二元一次方程组的解.
3.能根据简单的实际问题列出二元一次方程组.
问题1 什么是方程?
含有未知数的等式叫方程.
问题2 什么是一元一次方程?
只含有一个未知数(元),未知数的次数都是 1 ,且等号两边都是等式,这样的方程叫做一元一次方程.
新知一 二元一次方程(组)
篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分.某队在 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
解:设胜 x 场,则负(10-x)场.
2x +(10-x)= 16.
问题1 如何列一元一次方程?
问题2 设胜的场数是 x ,负的场数是 y ,你能用方程把这些条件
表示出来吗?
胜的场数 + 负的场数 = 总场数
胜的场数的分数 + 负的场数的分数 = 总分数
得分
10
场数
合计
负
胜
x
y
2x
y
16
2x+y=16
x+y=10
思考一:上述方程有什么特点
思考二:它与一元一次方程有什么不同
x+y=10
2x+y=16
含有两个未知数,并且含有未知数的项的次数都是 1 ,像这样的方程叫作二元一次方程.
注意:二元一次方程满足的三个条件:
(1)在方程中“元”是指未知数,“二元”就是指方程中有且只有两个未知数.
(2)“未知数的次数为 1 ”是指含有未知数的项(单项式)的次数是 1.
(3)二元一次方程的左边和右边都必须是整式.
方程组中有两个未知数,含有每个未知数的项的次数都是 1,并且一共有两个方程,像这样的方程组叫作二元一次方程组.
x+y=10,
2x+y=16
叫作方程组
小提示: 也是二元一次方程组.
例1 已知下列方程,其中是二元一次方程的有______________.
【解析】只有(1)(4)(5)(8)(10)满足二元一次方程的概念.
(2)为一元一次方程,方程中只含有一个未知数;
(3)中含未知数的项的次数为 2;(6)只含有一个未知数;
(7)不是整式方程;(9)中未知数 x 的次数为 2.
(1)(4)(5)(8)(10)
【解析】A 中未知数的项的次数为 2,故 A 不是二元一次方程组;
B 中含有三个未知数,故 B 不是二元一次方程组;
C 是二元一次方程组,故 C 是二元一次方程组;
D 不是整式方程,故 D 不是二元一次方程组.
例2 下列方程组是二元一次方程组的是( )
C
A. B. C. D.
x
y
探究 满足篮球联赛问题中的方程 x + y = 10 ,且符合问题
的实际意义的值有哪些?把它们填入表中.
x 0 1 2 3 4 5 6 7 8 9 10
y 10 9 8 7 6 5 4 3 2 1 0
新知二 二元一次方程组的解
思考二:上表中哪对 x,y 的值还满足方程 2x+y=16 ②?
x=6,y=4 还满足方程②.也就是说, 它是方程 x+y=10 ①
与方程②的公共解,记作
思考一:如果不考虑方程表示的实际意义,还可以取哪些值?这些值是有限的吗?
x,y 还可取到小数,如 x=0.5,y=9.5;有无数组这样的值.
一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
例3 下列数组中,是二元一次方程 x+y=7 的解的是( )
A.
C.
D.
B.
x=-2,
y=5
x=3,
y=4
x=-1,
y=7
x=-2,
y=-5
【思路点拨】二元一次方程 x+y=7 的解有无数个,
所以此题应该用排除法确定答案,分别代入方程组,使方程左右相等的解才是方程组的解.
B
例4 判断下列各组数是否是二元一次方程组 的解.
【总结升华】检验是否是方程组的解,应把数值代入两个方程,若两个方程同时成立,才是方程组的解;而方程组中某一个方程的某一组解不一定是方程组的解.
4x+2y=2, ①
x+2y=-1. ②
x=3,
y=-5
x=1,
y=-1
(1) (2)
√
例5 加工某种产品须经两道工序,第一道工序每人每天可完成 900 件,第二道工序每人每天可完成 1 200 件. 现有 7 位工人参加这两道工序,应怎样安排人力,才能使每天第一、二道工序所完成的件数相等?请列出符合题意的二元一次方程组.
解:设安排第一道工序为 x 人,第二道工序为 y 人.
根据题意得
1.关于 x,y 的方程 ax2+bx+2y=3 是一个二元一次方程,则 a,b 的值
分别为( )
A .a=0 且 b=0 B.a=0 或 b=0 C. a=0 且 b≠0 D.a≠0 且 b≠0
2.下列不是二元一次方程组的是( )
A.
x+y=3,
x-y=1
x+ =1,
y+x=2
B.
D.
6x+4y=9,
y=3x+4
C.
x=1,
y=1
B
C
3.二元一次方程组 的解是( )
A. B. C. D.
B
4.若方程 的一个解是 ,则 a=____ .
3
5.根据下列语句,分别设适当的未知数,列出二元一次方程或方程组.
(1)摩托车的时速是货车的 2 倍,它们的速度之和是 200 km/h;
(2)某种时装的价格是某种皮装价格的 1.4 倍,5 件皮装比 3 件时装贵 700 元.
x=2y,
x+y=200.
设摩托车的速度为 x km/h,货车的速度为 y km/h,则
设时装的价格为 x 元/件,皮装的价格为 y 元/件,则
x=1.4y,
5y=3x+700.
认识二元一次方程组
二元一次方程(组)的定义
二元一次方程(组)的解
列二元一次方程组
