8.3.3 几何图形与图表信息问题 课件 (共17张PPT)
文档属性
| 名称 | 8.3.3 几何图形与图表信息问题 课件 (共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
8.3.3 几何图形与图表信息问题
1.以含有多个未知数的实际问题为背景,经历“分析数量关系,设未知数,列方程组,解方程组和检验结果”的过程,体会方程组是刻画现实世界中含有多个未知数问题的数学模型;
2. 熟练掌握用方程组解决几何图形与图表信息等问题.
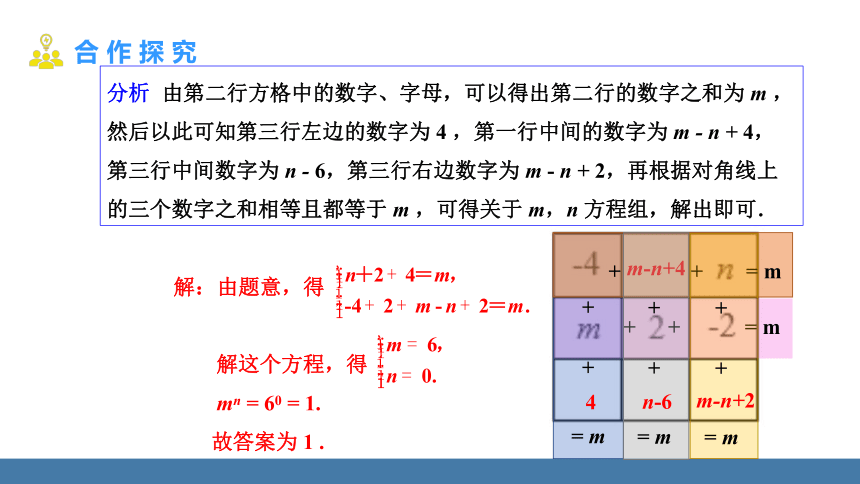
幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图 1),将 9 个数填在 3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图 2 的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则 mn = ___________.
问题1 “每个横行、每个竖列、每条对角线上的三个数字之和都相等”怎么理解呢?
问题2 突破口在哪里呢?
分析 由第二行方格中的数字、字母,可以得出第二行的数字之和为 m ,然后以此可知第三行左边的数字为 4 ,第一行中间的数字为 m - n + 4,第三行中间数字为 n - 6,第三行右边数字为 m - n + 2,再根据对角线上的三个数字之和相等且都等于 m ,可得关于 m,n 方程组,解出即可.
解:由题意,得
解这个方程,得
mn = 60 = 1.
故答案为 1 .
+ + = m
+
+
= m
4
+ + = m
m-n+4
+
+
= m
n-6
+
+
= m
m-n+2
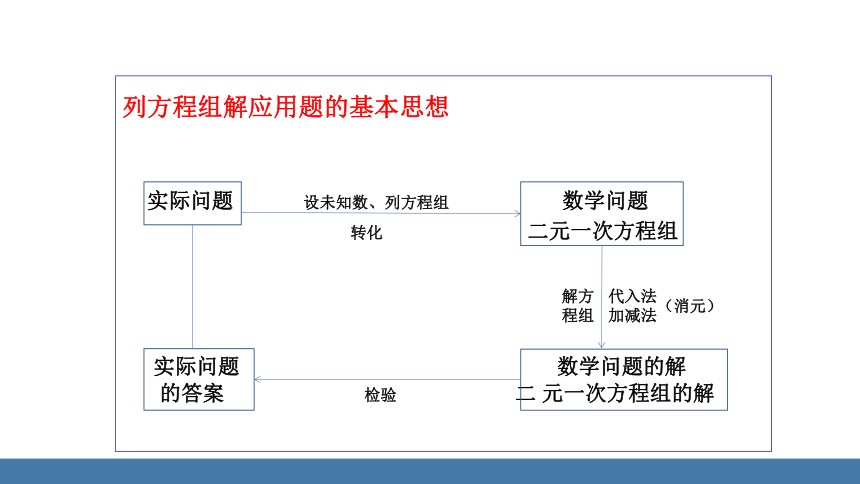
列方程组解应用题的基本思想
实际问题 设未知数、列方程组 数学问题
转化 二元一次方程组
实际问题 数学问题的解
的答案 检验 二 元一次方程组的解
解方程组
代入法
加减法
(消元)
列二元一次方程组解应用题的一般步骤
设:用两个字母表示问题中的两个未知数;
列:列出方程组(分析题意,找出两个等量关系,根据等量关系列出方程组);
解:解方程组,求出未知数的值;
验:检验求得的值是否正确和符合实际情形;
答:写出答案.
类型一 几何图形问题
1. 在长方形ABCD中,放入六个形状、大小相同的长方形,所标尺寸如图所示,求图中阴影部分的面积.
等量关系:
长 + 3 × 宽 = 14.
6 + 2 × 宽 = 长 + 宽.
解:设小长方形的长是 x cm ,宽是 y cm.
根据问题中的数量关系,列方程组
解这个方程组,得
∴小长方形的长是 8 cm ,宽是 2 cm.
S阴影部分 = S四边形ABCD - 6 × S小长方形 = 14 × 10 - 6 × 2 × 8 = 44 cm2.
答:阴影部分的面积是 44 cm2.
某厂计划生产 A,B 两种产品 600 件,已知两种产品的成本价和销售价如下表:
(1)若该厂生产 600 件 A,B 两种产品时,恰好用了 2 300 元,求两种产品各生产了多少件.
(2)若该厂销售完 600 件 A,B 两种产品时,要使利润恰好是成本价的30%,应如何安排生产?此时利润为多少元?(利润=销售价-成本价)
类型二 图表信息问题
A种产品 B种产品
成本价/(元/件) 2.5 4.5
销售价/(元/件) 3 6
解:(1)设 A种产品生产了 x 个,B种产品生产了 y 个.
由题意,列方程组
解这个方程组,得
答:A种产品生产了 200 个,B种产品生产了 400 个.
返回
解:(2)设 A 种产品生产了 m 个,B 种产品生产了 n 个.
由题意,列方程组
解这个方程组,得
(3-2.5)×225+(6-4.5)×375=675(元).
答:应安排生产 A 种产品 225 件,B 种产品 375 件,此时利润为 675 元.
1. 在长为 10 m,宽为 8 m 的长方形空地上,沿平行于长方形各边的方向分割出三个全等的小长方形花圃,其示意图如图所示. 求花圃的面积.
解:设花圃的长是 x m,宽是 y m.
根据题意,得
解这个方程,得
花圃的面积 = 3 xy = 3 × 4 × 2 = 24 m2.
答:花圃的面积是 24 m2 .
2. 如图所示的是由截面为同一种长方形的墙砖粘贴的部分墙面,其中三块横放的墙砖比两块竖放的墙砖低,两块竖放的墙砖比两块横放的墙砖高,求每块墙砖的截面面积.
解:设每块墙砖的长为 x cm, 宽为 y cm.
根据题意,得
解这个方程,得
每块墙砖的截面面积 = 45 × 20 = 900 cm2.
答:每块墙砖的截面面积是 900 cm2.
3.某地区 2020 年进出口总额为 520 亿元,2021 年进出口总额比 2020 年有所增加,其中进口额增加了 25%,出口额增加了 30%. (进出口总额 = 进口额 + 出口额)
(1)设 2020 年进口额为 x 亿元,出口额为 y 亿元,请用含 x,y 的式子填表:
年份 进口额/亿元 出口额/亿元 进出口总额/亿元
2020 x y 520
2021 1.25x 1.3y
1.25 x+1.3 y
(2)已知2021年进出口总额比 2020 年增加了 140 亿元,求 2021 年进口额和出口额分别是多少亿元.
∴1.25 x = 400,1.3 y = 260.
答:2021年进口额是400亿元,出口额是260亿元.
解:由题意可得,
解这个方程,得
二元一次方程组应用
几何图形问题
图表信息问题
8.3.3 几何图形与图表信息问题
1.以含有多个未知数的实际问题为背景,经历“分析数量关系,设未知数,列方程组,解方程组和检验结果”的过程,体会方程组是刻画现实世界中含有多个未知数问题的数学模型;
2. 熟练掌握用方程组解决几何图形与图表信息等问题.
幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图 1),将 9 个数填在 3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图 2 的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则 mn = ___________.
问题1 “每个横行、每个竖列、每条对角线上的三个数字之和都相等”怎么理解呢?
问题2 突破口在哪里呢?
分析 由第二行方格中的数字、字母,可以得出第二行的数字之和为 m ,然后以此可知第三行左边的数字为 4 ,第一行中间的数字为 m - n + 4,第三行中间数字为 n - 6,第三行右边数字为 m - n + 2,再根据对角线上的三个数字之和相等且都等于 m ,可得关于 m,n 方程组,解出即可.
解:由题意,得
解这个方程,得
mn = 60 = 1.
故答案为 1 .
+ + = m
+
+
= m
4
+ + = m
m-n+4
+
+
= m
n-6
+
+
= m
m-n+2
列方程组解应用题的基本思想
实际问题 设未知数、列方程组 数学问题
转化 二元一次方程组
实际问题 数学问题的解
的答案 检验 二 元一次方程组的解
解方程组
代入法
加减法
(消元)
列二元一次方程组解应用题的一般步骤
设:用两个字母表示问题中的两个未知数;
列:列出方程组(分析题意,找出两个等量关系,根据等量关系列出方程组);
解:解方程组,求出未知数的值;
验:检验求得的值是否正确和符合实际情形;
答:写出答案.
类型一 几何图形问题
1. 在长方形ABCD中,放入六个形状、大小相同的长方形,所标尺寸如图所示,求图中阴影部分的面积.
等量关系:
长 + 3 × 宽 = 14.
6 + 2 × 宽 = 长 + 宽.
解:设小长方形的长是 x cm ,宽是 y cm.
根据问题中的数量关系,列方程组
解这个方程组,得
∴小长方形的长是 8 cm ,宽是 2 cm.
S阴影部分 = S四边形ABCD - 6 × S小长方形 = 14 × 10 - 6 × 2 × 8 = 44 cm2.
答:阴影部分的面积是 44 cm2.
某厂计划生产 A,B 两种产品 600 件,已知两种产品的成本价和销售价如下表:
(1)若该厂生产 600 件 A,B 两种产品时,恰好用了 2 300 元,求两种产品各生产了多少件.
(2)若该厂销售完 600 件 A,B 两种产品时,要使利润恰好是成本价的30%,应如何安排生产?此时利润为多少元?(利润=销售价-成本价)
类型二 图表信息问题
A种产品 B种产品
成本价/(元/件) 2.5 4.5
销售价/(元/件) 3 6
解:(1)设 A种产品生产了 x 个,B种产品生产了 y 个.
由题意,列方程组
解这个方程组,得
答:A种产品生产了 200 个,B种产品生产了 400 个.
返回
解:(2)设 A 种产品生产了 m 个,B 种产品生产了 n 个.
由题意,列方程组
解这个方程组,得
(3-2.5)×225+(6-4.5)×375=675(元).
答:应安排生产 A 种产品 225 件,B 种产品 375 件,此时利润为 675 元.
1. 在长为 10 m,宽为 8 m 的长方形空地上,沿平行于长方形各边的方向分割出三个全等的小长方形花圃,其示意图如图所示. 求花圃的面积.
解:设花圃的长是 x m,宽是 y m.
根据题意,得
解这个方程,得
花圃的面积 = 3 xy = 3 × 4 × 2 = 24 m2.
答:花圃的面积是 24 m2 .
2. 如图所示的是由截面为同一种长方形的墙砖粘贴的部分墙面,其中三块横放的墙砖比两块竖放的墙砖低,两块竖放的墙砖比两块横放的墙砖高,求每块墙砖的截面面积.
解:设每块墙砖的长为 x cm, 宽为 y cm.
根据题意,得
解这个方程,得
每块墙砖的截面面积 = 45 × 20 = 900 cm2.
答:每块墙砖的截面面积是 900 cm2.
3.某地区 2020 年进出口总额为 520 亿元,2021 年进出口总额比 2020 年有所增加,其中进口额增加了 25%,出口额增加了 30%. (进出口总额 = 进口额 + 出口额)
(1)设 2020 年进口额为 x 亿元,出口额为 y 亿元,请用含 x,y 的式子填表:
年份 进口额/亿元 出口额/亿元 进出口总额/亿元
2020 x y 520
2021 1.25x 1.3y
1.25 x+1.3 y
(2)已知2021年进出口总额比 2020 年增加了 140 亿元,求 2021 年进口额和出口额分别是多少亿元.
∴1.25 x = 400,1.3 y = 260.
答:2021年进口额是400亿元,出口额是260亿元.
解:由题意可得,
解这个方程,得
二元一次方程组应用
几何图形问题
图表信息问题
