8.3.4 打折销售及其他问题 课件 (共20张PPT)
文档属性
| 名称 | 8.3.4 打折销售及其他问题 课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 939.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 12:18:36 | ||
图片预览







文档简介
(共20张PPT)
8.3.4 打折销售及其他问题
1.以含有多个未知数的实际问题为背景,经历“分析数量关系,设未知数,列方程组,解方程组和检验结果”的过程,体会方程组是刻画现实世界中含有多个未知数问题的数学模型;
2. 熟练掌握用方程组解决打折销售及其他等问题.
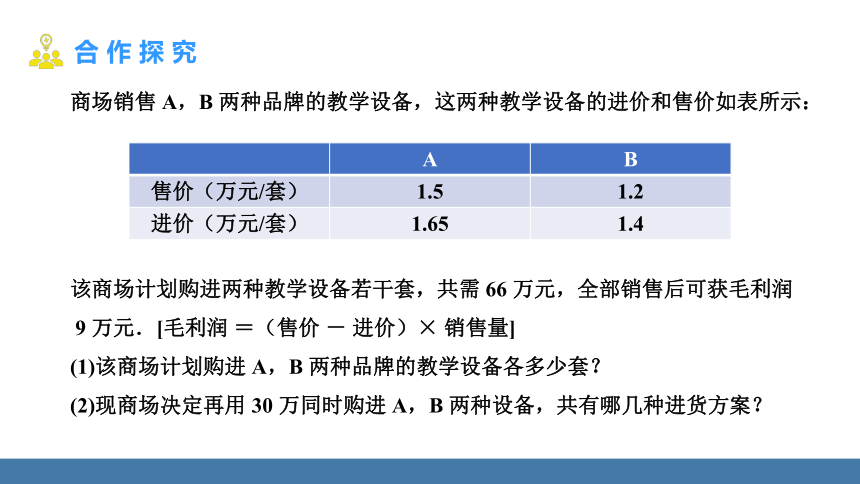
商场销售 A,B 两种品牌的教学设备,这两种教学设备的进价和售价如表所示:
该商场计划购进两种教学设备若干套,共需 66 万元,全部销售后可获毛利润
9 万元.[毛利润 =(售价 - 进价)× 销售量]
(1)该商场计划购进 A,B 两种品牌的教学设备各多少套?
(2)现商场决定再用 30 万同时购进 A,B 两种设备,共有哪几种进货方案?
A B
售价(万元/套) 1.5 1.2
进价(万元/套) 1.65 1.4
解:(1)设购进 A 品牌的教学设备 x 套,B 品牌的教学设备 y 套.
由题意,列方程组
解这个方程组,得
答:购进 A 品牌的教学设备 20 套,B 品牌的教学设备 30 套.
返回
解:(2)设可以购进 m 套 A 品牌的教学设备,n 套 B 品牌的教学设备.
依题意,得 1.5 m + 1.2 n = 30 ,
∴
又∵ m,n 均为正整数,
∴
∴共有 4 种进货方案,
方案 1:购进 16 套 A 品牌的教学设备,5 套 B 品牌的教学设备;
方案 2:购进 12套 A 品牌的教学设备,10套 B 品牌的教学设备;
方案 3:购进 8 套 A 品牌的教学设备,15套 B 品牌的教学设备;
方案 4:购进 4 套 A 品牌的教学设备,20套 B 品牌的教学设备.
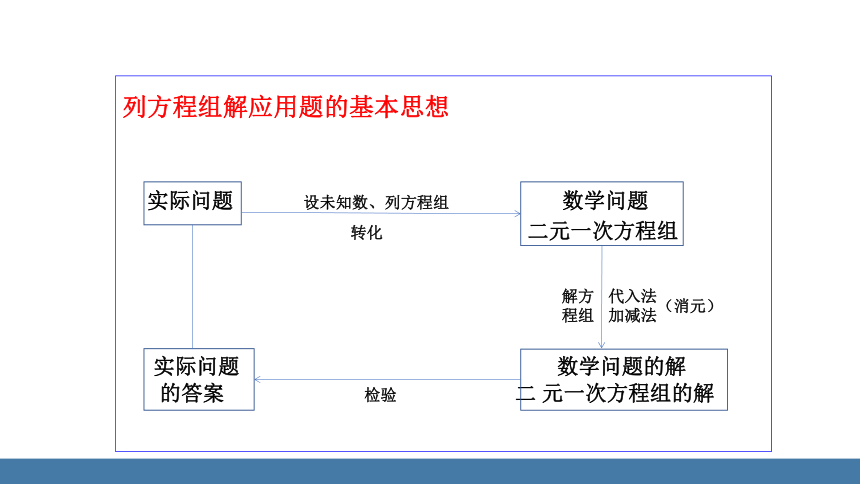
列方程组解应用题的基本思想
实际问题 设未知数、列方程组 数学问题
转化 二元一次方程组
实际问题 数学问题的解
的答案 检验 二 元一次方程组的解
解方程组
代入法
加减法
(消元)
列二元一次方程组解应用题的一般步骤
设:用两个字母表示问题中的两个未知数;
列:列出方程组(分析题意,找出两个等量关系,根据等量关系列出方程组);
解:解方程组,求出未知数的值;
验:检验求得的值是否正确和符合实际情形;
答:写出答案.
某超市对甲、乙两种商品进行打折销售,其中甲种商品打八折,乙种商品打七五折.已知打折前,买 6 件甲种商品和 3 件乙种商品需 600 元; 打折后,买 50 件甲种商品和 40 件乙种商品需 5 200 元.求打折前甲、乙两种商品每件分别为多少元.
类型一 打折问题
等量关系:
打折前:6×甲 +3× 乙 = 600 元.
打折后:50×甲 +40× 乙 = 5200 元.
解:设打折前甲商品每件 x 元,甲商品每件 y 元.
由题意,列方程组
解这个方程组,得
答:打折前甲商品每件 40 元,甲商品每件 120 元.
返回
类型二 销售问题
1. 王师傅下岗后开了一家小商店,上周他购进甲乙两种商品共 50 件,甲种商品的进价是每件 35 元,利润率是 20%,乙种商品的进价是每件 20 元,利润率是 15%,共获利 278 元,你知道王师傅分别购进甲乙两种商品各多少件吗
等量关系:
甲 + 乙 = 50 件.
解:设王师傅购进甲商品 x 件,购进乙商品 y 件.
由题意,得
解这个方程组,得
答:王师傅购进甲商品 32 件,购进乙商品 18 件.
类型三 配置问题
1. 用含药 30% 和 75% 的两种防腐药水,配置含药 50% 的防腐药水 18 kg,
两种药水各需多少千克?
等量关系:
需 30% 的药水 + 需 75% 的药水 = 18 kg.
配好后的含药量 = 含药 30% 的含药量 + 含药 75% 的含药量.
解:设含药 30% 的防腐药水需要 x kg,含药75%的防腐药水需要 y kg.
由题意,得
解这个方程组,得
答:含药 30% 的防腐药水需要 10 kg,含药75%的防腐药水需要 8 kg.
类型四 数字问题
小明和小亮做游戏,小明在一个加数的后面多写了一个 0,得到的和为 242;小亮在另一个加数后面多写了一个 0,得到的和为 341 . 原来的两个数分别为多少?
【思路点拨】在后面多写一个 0,实际就是扩大了 10 倍.
【等量关系】
10 × 一个加数 + 另一个加数 = 242;
一个加数 + 10 × 另一个加数 = 341.
解:设原来的两个数分别为 x 和 y .
由题意,得
解这个方程组,得
答:原来的两个数分别为 21 和 32 .
1.某商场投入 13 800 元资金购进甲、乙两种矿泉水共 500 箱,矿泉水的成本价和销售价如表所示:
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完 500 箱矿泉水,该商场共获得利润多少元?
成本价/(元/箱) 销售价/(元/箱)
甲 24 36
乙 33 48
解:(1)设商场购进甲种矿泉水 x 箱,购进乙种矿泉水 y 箱.
由题意,得
解这个方程,得
答:商场购进甲种矿泉水 300 箱,购进乙种矿泉水 200 箱.
(2)300 ×(36 - 24)+ 200 ×(48 - 33)
= 3600 + 3000 = 6600(元).
答:该商场共获得利润 6600 元.
2. 某便利店准备用两种价格分别为 36 元/kg 和 21 元/kg 的糖果混合成杂拌糖果出售,混合后糖果的价格是 30 元/kg.现在要配置这种杂拌糖果 100 kg 需要两种糖果各多少千克?
解:设需要每千克为 36 元的糖果 x kg,每千克为 21 元的糖果 y kg.
根据题意,得
解这个方程,得
答:需要每千克为 36 元的糖果 60 kg,每千克为 21 元的糖果 40 kg.
3.一个两位数十位上的数字是个位上的数字为 2 倍,若交换十位与个位上的数字,则所得新两位数与原数的和为 99 ,求这个两位数.
∴ 10 x + y = 10 × 6 + 3 = 63.
答:这个两位数是 63 .
解:设这个两位数十位上的数字是 x ,个位上的数字是 y ,
由题意,得
解这个方程,得
二元一次方程组应用
打折销售问题
其他问题
8.3.4 打折销售及其他问题
1.以含有多个未知数的实际问题为背景,经历“分析数量关系,设未知数,列方程组,解方程组和检验结果”的过程,体会方程组是刻画现实世界中含有多个未知数问题的数学模型;
2. 熟练掌握用方程组解决打折销售及其他等问题.
商场销售 A,B 两种品牌的教学设备,这两种教学设备的进价和售价如表所示:
该商场计划购进两种教学设备若干套,共需 66 万元,全部销售后可获毛利润
9 万元.[毛利润 =(售价 - 进价)× 销售量]
(1)该商场计划购进 A,B 两种品牌的教学设备各多少套?
(2)现商场决定再用 30 万同时购进 A,B 两种设备,共有哪几种进货方案?
A B
售价(万元/套) 1.5 1.2
进价(万元/套) 1.65 1.4
解:(1)设购进 A 品牌的教学设备 x 套,B 品牌的教学设备 y 套.
由题意,列方程组
解这个方程组,得
答:购进 A 品牌的教学设备 20 套,B 品牌的教学设备 30 套.
返回
解:(2)设可以购进 m 套 A 品牌的教学设备,n 套 B 品牌的教学设备.
依题意,得 1.5 m + 1.2 n = 30 ,
∴
又∵ m,n 均为正整数,
∴
∴共有 4 种进货方案,
方案 1:购进 16 套 A 品牌的教学设备,5 套 B 品牌的教学设备;
方案 2:购进 12套 A 品牌的教学设备,10套 B 品牌的教学设备;
方案 3:购进 8 套 A 品牌的教学设备,15套 B 品牌的教学设备;
方案 4:购进 4 套 A 品牌的教学设备,20套 B 品牌的教学设备.
列方程组解应用题的基本思想
实际问题 设未知数、列方程组 数学问题
转化 二元一次方程组
实际问题 数学问题的解
的答案 检验 二 元一次方程组的解
解方程组
代入法
加减法
(消元)
列二元一次方程组解应用题的一般步骤
设:用两个字母表示问题中的两个未知数;
列:列出方程组(分析题意,找出两个等量关系,根据等量关系列出方程组);
解:解方程组,求出未知数的值;
验:检验求得的值是否正确和符合实际情形;
答:写出答案.
某超市对甲、乙两种商品进行打折销售,其中甲种商品打八折,乙种商品打七五折.已知打折前,买 6 件甲种商品和 3 件乙种商品需 600 元; 打折后,买 50 件甲种商品和 40 件乙种商品需 5 200 元.求打折前甲、乙两种商品每件分别为多少元.
类型一 打折问题
等量关系:
打折前:6×甲 +3× 乙 = 600 元.
打折后:50×甲 +40× 乙 = 5200 元.
解:设打折前甲商品每件 x 元,甲商品每件 y 元.
由题意,列方程组
解这个方程组,得
答:打折前甲商品每件 40 元,甲商品每件 120 元.
返回
类型二 销售问题
1. 王师傅下岗后开了一家小商店,上周他购进甲乙两种商品共 50 件,甲种商品的进价是每件 35 元,利润率是 20%,乙种商品的进价是每件 20 元,利润率是 15%,共获利 278 元,你知道王师傅分别购进甲乙两种商品各多少件吗
等量关系:
甲 + 乙 = 50 件.
解:设王师傅购进甲商品 x 件,购进乙商品 y 件.
由题意,得
解这个方程组,得
答:王师傅购进甲商品 32 件,购进乙商品 18 件.
类型三 配置问题
1. 用含药 30% 和 75% 的两种防腐药水,配置含药 50% 的防腐药水 18 kg,
两种药水各需多少千克?
等量关系:
需 30% 的药水 + 需 75% 的药水 = 18 kg.
配好后的含药量 = 含药 30% 的含药量 + 含药 75% 的含药量.
解:设含药 30% 的防腐药水需要 x kg,含药75%的防腐药水需要 y kg.
由题意,得
解这个方程组,得
答:含药 30% 的防腐药水需要 10 kg,含药75%的防腐药水需要 8 kg.
类型四 数字问题
小明和小亮做游戏,小明在一个加数的后面多写了一个 0,得到的和为 242;小亮在另一个加数后面多写了一个 0,得到的和为 341 . 原来的两个数分别为多少?
【思路点拨】在后面多写一个 0,实际就是扩大了 10 倍.
【等量关系】
10 × 一个加数 + 另一个加数 = 242;
一个加数 + 10 × 另一个加数 = 341.
解:设原来的两个数分别为 x 和 y .
由题意,得
解这个方程组,得
答:原来的两个数分别为 21 和 32 .
1.某商场投入 13 800 元资金购进甲、乙两种矿泉水共 500 箱,矿泉水的成本价和销售价如表所示:
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完 500 箱矿泉水,该商场共获得利润多少元?
成本价/(元/箱) 销售价/(元/箱)
甲 24 36
乙 33 48
解:(1)设商场购进甲种矿泉水 x 箱,购进乙种矿泉水 y 箱.
由题意,得
解这个方程,得
答:商场购进甲种矿泉水 300 箱,购进乙种矿泉水 200 箱.
(2)300 ×(36 - 24)+ 200 ×(48 - 33)
= 3600 + 3000 = 6600(元).
答:该商场共获得利润 6600 元.
2. 某便利店准备用两种价格分别为 36 元/kg 和 21 元/kg 的糖果混合成杂拌糖果出售,混合后糖果的价格是 30 元/kg.现在要配置这种杂拌糖果 100 kg 需要两种糖果各多少千克?
解:设需要每千克为 36 元的糖果 x kg,每千克为 21 元的糖果 y kg.
根据题意,得
解这个方程,得
答:需要每千克为 36 元的糖果 60 kg,每千克为 21 元的糖果 40 kg.
3.一个两位数十位上的数字是个位上的数字为 2 倍,若交换十位与个位上的数字,则所得新两位数与原数的和为 99 ,求这个两位数.
∴ 10 x + y = 10 × 6 + 3 = 63.
答:这个两位数是 63 .
解:设这个两位数十位上的数字是 x ,个位上的数字是 y ,
由题意,得
解这个方程,得
二元一次方程组应用
打折销售问题
其他问题
