8.4.2三元一次方程组的应用 课件 (共18张PPT)
文档属性
| 名称 | 8.4.2三元一次方程组的应用 课件 (共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 951.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
* 8.4.2 三元一次方程组的应用
1.理解三元一次方程组的概念.
2.掌握解三元一次方程组过程中化三元为二元或一元的思路.
3. 熟练掌握用三元一次方程组解决实际问题.
1.什么是三元一次方程?那三元一次方程组呢?
①三元一次方程:
含有三个未知数,并且含有未知数的项的次数都是 1 的整式方程.
2.解三元一次方程组的基本思路是什么?
②三元一次方程组:
含有三个未知数,每个方程中含未知数的项的次数都是 1 ,并且一共有三个方程.
消元
消元
三元一次方程组 三元一次方程组 三元一次方程组
(2022·湖北武汉)幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将 9 个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的 3 个数之和相等,例如图(1)就是一个幻方.
图(2)是一个未完成的幻方,求 x + y.
4 9 2
3 5 7
8 1 6
x 6 20
22 y
(1) (2)
问题1 “每个横行、每个竖列、每条对角线上的三个数字之和都相等”怎么理解呢?
问题2 突破口在哪里呢?
x 6 20
22 y
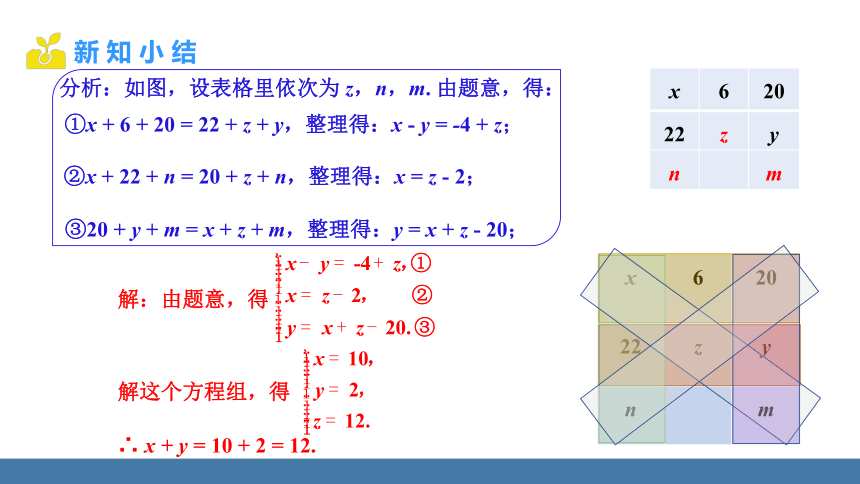
分析:如图,设表格里依次为 z,n,m. 由题意,得:
x 6 20
22 z y
n m
x 6 20
22 z y
n m
②x + 22 + n = 20 + z + n,整理得:x = z - 2;
①x + 6 + 20 = 22 + z + y,整理得:x - y = -4 + z;
解:由题意,得
解这个方程组,得
∴ x + y = 10 + 2 = 12.
③20 + y + m = x + z + m,整理得:y = x + z - 20;
三元一次方程组的解法
(1)解三元一次方程组的基本思路是:通过“代入”或“加减”消元,把“三元”化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程.这与解二元一次方程组是一样的.其思想方法是:
三元一次方程组 二元一次方程组 一元一次方程组
(2)有些特殊的方程组可用特殊的消元法,解题时要根据各方程特点寻求其较简单的解法.
消元
消元
列三元一次方程组解应用题的一般步骤
1.弄清题意和题目中的数量关系,用字母(如 x,y,z )表示题目中的两个(或三个)未知数;
2.找出能够表达应用题全部含义的相等关系;
3.根据这些相等关系列出需要的代数式,从而列出方程并组成方程组;
4.解这个方程组,求出未知数的值;
5.写出答案(包括单位名称).
注意:解实际应用题必须写“答”,而且在写答案前要根据应用题的实际意义,检查求得的结果是否合理,不符合题意的应该舍去.
例1 甲、乙、丙三个数的和是 35,甲数的 2 倍比乙数大 5,乙数的 等于丙数的 .求这三个数.
数量关系:
(1)甲 + 乙 +丙 = 35 .
(2)甲 × 2 = 乙 + 5.
(3)
例1 甲、乙、丙三个数的和是 35,甲数的 2 倍比乙数大 5,乙数的 等于丙数的 .求这三个数.
解:设甲为 x ,乙为 y ,丙为 z .
由题意,得
解这个方程组,得
答:甲是 10,乙是 15,丙是 10.
例 2 某电脑公司有 A型、B型、C型三种型号的电脑,其中 A型每台6 000 元、
B型每台 4 000 元、C型每台 2 500 元.某中学现有资金 100 500元,计划全部用于从这家电脑公司购进 36 台两种型号的电脑.请你设计几种不同的购买方案供这个学校选择,并说明理由.
【分析】
两种型号共 36 台,共有资金 100 500 元;
所以分类讨论,舍弃负数、小数值,即可解答此题.
解:设购买 A 型电脑 x 台,B 型 y 台,C 型 z 台.
(1)若购买 A 型、B 型时,由题意,得
解得 不符合题意,舍去.
(2)若购买 A 型、C 型时,由题意,得
解得
(3)若购买 B 型、C 型时,由题意,得
解得
答:有两种方案供该校选择,第一种方案是购进 A 型电脑 3 台,
C 型电脑 33 台;第二种方案是购进 B 型电脑 7 台,C 型电脑 29 台.
例3 甲地到乙地全程是 3.3 km,一段上坡、一段平路、一段下坡.如果保持上坡每小时走 3 km,平路每小时走 4 km,下坡每小时走 5 km,那么从甲地到乙地需 0.85 h,从乙地到甲地需 0.89 h.从甲地到乙地时,上坡、平路、下坡的路程各是多少?
【分析】
路程 = 速度 × 时间,时间 = 路程 ÷ 速度
解:设从甲地到乙地,上坡路是 x km,平路是 y km,下坡路是 z km.
根据题意,得
解这个方程,得
答:从甲地到乙地,上坡路是 1.2 km,平路是 0.6 km,下坡路是 1.5 km.
1.一个三位数,个位、百位上的数的和等于十位上的数,百位上的数
的 7 倍比个位、十位上的数的和大 2,且个位、十位、百位上的数的和
是 14. 求这个三位数.
解:设这个三位数百位上的数是 x ,十位是 y ,个位是 z.
根据题意,得
解这个方程,得
答:这个三位数是275.
D
2.甲、乙、丙三种商品,若购买甲 2 件、乙 4 件、丙3 件,共需 220 元钱;购甲 3 件、乙 1 件、丙 2 件共需 235 元钱.那么购甲、乙、丙三种商品各一件共需( )
A.85元 B.89元 C.90元 D.91元
【小结】注意观察方程组的特征,
运用整体思想是解题的关键.
解析:设购甲商品 x 件 ,乙商品 y 件,丙商品 z 件.
根据题意,得
两式相加,得 5x + 5y + 5z = 455 .
解得 x + y + z = 91.
所以购三种商品各一件需 91 元.
3.某服装厂专门安排 210 名工人进行手工衬衣的缝制,每件衬衣由 2 个衣袖、1 个衣身、1 个衣领组成. 如果每人每天能够缝制衣袖 10 个, 或衣身 15个,或衣领 12 个,那么应该如何安排工人,使每天缝制出的衣袖、衣身、衣领正好配套?
解:设应该安排 x 名工人缝制衣袖,y 名工人缝制衣身,z 名工人缝制衣领.
根据题意,得 解得
答:应该安排 120 名工人缝制衣袖,40 名工人缝制衣身,50 名工人缝制衣领.
三元一次
方程组应用
步骤
方法
* 8.4.2 三元一次方程组的应用
1.理解三元一次方程组的概念.
2.掌握解三元一次方程组过程中化三元为二元或一元的思路.
3. 熟练掌握用三元一次方程组解决实际问题.
1.什么是三元一次方程?那三元一次方程组呢?
①三元一次方程:
含有三个未知数,并且含有未知数的项的次数都是 1 的整式方程.
2.解三元一次方程组的基本思路是什么?
②三元一次方程组:
含有三个未知数,每个方程中含未知数的项的次数都是 1 ,并且一共有三个方程.
消元
消元
三元一次方程组 三元一次方程组 三元一次方程组
(2022·湖北武汉)幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将 9 个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的 3 个数之和相等,例如图(1)就是一个幻方.
图(2)是一个未完成的幻方,求 x + y.
4 9 2
3 5 7
8 1 6
x 6 20
22 y
(1) (2)
问题1 “每个横行、每个竖列、每条对角线上的三个数字之和都相等”怎么理解呢?
问题2 突破口在哪里呢?
x 6 20
22 y
分析:如图,设表格里依次为 z,n,m. 由题意,得:
x 6 20
22 z y
n m
x 6 20
22 z y
n m
②x + 22 + n = 20 + z + n,整理得:x = z - 2;
①x + 6 + 20 = 22 + z + y,整理得:x - y = -4 + z;
解:由题意,得
解这个方程组,得
∴ x + y = 10 + 2 = 12.
③20 + y + m = x + z + m,整理得:y = x + z - 20;
三元一次方程组的解法
(1)解三元一次方程组的基本思路是:通过“代入”或“加减”消元,把“三元”化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程.这与解二元一次方程组是一样的.其思想方法是:
三元一次方程组 二元一次方程组 一元一次方程组
(2)有些特殊的方程组可用特殊的消元法,解题时要根据各方程特点寻求其较简单的解法.
消元
消元
列三元一次方程组解应用题的一般步骤
1.弄清题意和题目中的数量关系,用字母(如 x,y,z )表示题目中的两个(或三个)未知数;
2.找出能够表达应用题全部含义的相等关系;
3.根据这些相等关系列出需要的代数式,从而列出方程并组成方程组;
4.解这个方程组,求出未知数的值;
5.写出答案(包括单位名称).
注意:解实际应用题必须写“答”,而且在写答案前要根据应用题的实际意义,检查求得的结果是否合理,不符合题意的应该舍去.
例1 甲、乙、丙三个数的和是 35,甲数的 2 倍比乙数大 5,乙数的 等于丙数的 .求这三个数.
数量关系:
(1)甲 + 乙 +丙 = 35 .
(2)甲 × 2 = 乙 + 5.
(3)
例1 甲、乙、丙三个数的和是 35,甲数的 2 倍比乙数大 5,乙数的 等于丙数的 .求这三个数.
解:设甲为 x ,乙为 y ,丙为 z .
由题意,得
解这个方程组,得
答:甲是 10,乙是 15,丙是 10.
例 2 某电脑公司有 A型、B型、C型三种型号的电脑,其中 A型每台6 000 元、
B型每台 4 000 元、C型每台 2 500 元.某中学现有资金 100 500元,计划全部用于从这家电脑公司购进 36 台两种型号的电脑.请你设计几种不同的购买方案供这个学校选择,并说明理由.
【分析】
两种型号共 36 台,共有资金 100 500 元;
所以分类讨论,舍弃负数、小数值,即可解答此题.
解:设购买 A 型电脑 x 台,B 型 y 台,C 型 z 台.
(1)若购买 A 型、B 型时,由题意,得
解得 不符合题意,舍去.
(2)若购买 A 型、C 型时,由题意,得
解得
(3)若购买 B 型、C 型时,由题意,得
解得
答:有两种方案供该校选择,第一种方案是购进 A 型电脑 3 台,
C 型电脑 33 台;第二种方案是购进 B 型电脑 7 台,C 型电脑 29 台.
例3 甲地到乙地全程是 3.3 km,一段上坡、一段平路、一段下坡.如果保持上坡每小时走 3 km,平路每小时走 4 km,下坡每小时走 5 km,那么从甲地到乙地需 0.85 h,从乙地到甲地需 0.89 h.从甲地到乙地时,上坡、平路、下坡的路程各是多少?
【分析】
路程 = 速度 × 时间,时间 = 路程 ÷ 速度
解:设从甲地到乙地,上坡路是 x km,平路是 y km,下坡路是 z km.
根据题意,得
解这个方程,得
答:从甲地到乙地,上坡路是 1.2 km,平路是 0.6 km,下坡路是 1.5 km.
1.一个三位数,个位、百位上的数的和等于十位上的数,百位上的数
的 7 倍比个位、十位上的数的和大 2,且个位、十位、百位上的数的和
是 14. 求这个三位数.
解:设这个三位数百位上的数是 x ,十位是 y ,个位是 z.
根据题意,得
解这个方程,得
答:这个三位数是275.
D
2.甲、乙、丙三种商品,若购买甲 2 件、乙 4 件、丙3 件,共需 220 元钱;购甲 3 件、乙 1 件、丙 2 件共需 235 元钱.那么购甲、乙、丙三种商品各一件共需( )
A.85元 B.89元 C.90元 D.91元
【小结】注意观察方程组的特征,
运用整体思想是解题的关键.
解析:设购甲商品 x 件 ,乙商品 y 件,丙商品 z 件.
根据题意,得
两式相加,得 5x + 5y + 5z = 455 .
解得 x + y + z = 91.
所以购三种商品各一件需 91 元.
3.某服装厂专门安排 210 名工人进行手工衬衣的缝制,每件衬衣由 2 个衣袖、1 个衣身、1 个衣领组成. 如果每人每天能够缝制衣袖 10 个, 或衣身 15个,或衣领 12 个,那么应该如何安排工人,使每天缝制出的衣袖、衣身、衣领正好配套?
解:设应该安排 x 名工人缝制衣袖,y 名工人缝制衣身,z 名工人缝制衣领.
根据题意,得 解得
答:应该安排 120 名工人缝制衣袖,40 名工人缝制衣身,50 名工人缝制衣领.
三元一次
方程组应用
步骤
方法
