9.1.2 不等式的性质(2) 课件 (共14张PPT)
文档属性
| 名称 | 9.1.2 不等式的性质(2) 课件 (共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-26 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第九章 不等式与不等式组
9.1.2 不等式的性质(2)
问题 前面学过哪几种形式的不等式?
xm, x≠m.
思考 写出下列图片信息中的含义:
问题 铁路部门对随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过160cm.设行李的长、宽、高分别为acm,bcm,ccm,请你列出行李的长、宽、高满足的关系式.
根据题意可得: a+b+c≤160.
我们把用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.其中“≥”读作“大于等于”,“≤”读作“小于等于”.
1.不等式的概念
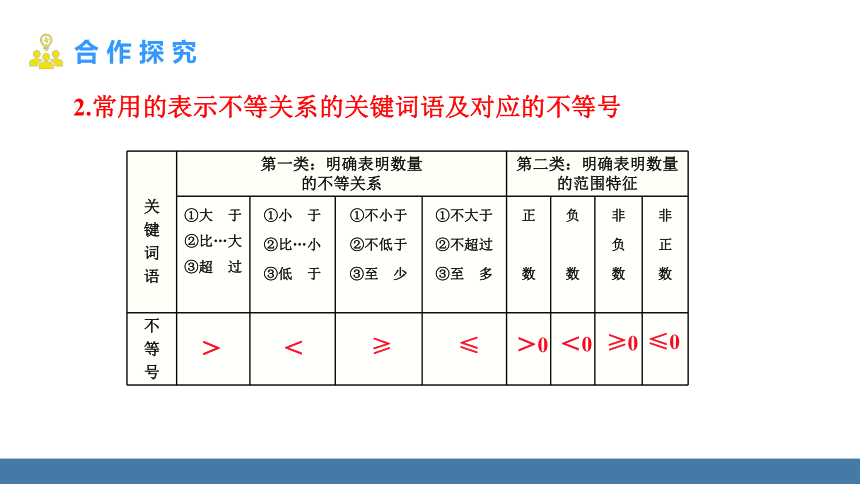
2.常用的表示不等关系的关键词语及对应的不等号
关 键 词 语 第一类:明确表明数量 的不等关系 第二类:明确表明数量的范围特征 ①大 于 ②比…大 ③超 过 ①小 于 ②比…小 ③低 于 ①不小于 ②不低于 ③至 少 ①不大于 ②不超过 ③至 多 正 数 负 数 非 负 数 非
正
数
不 等 号
<
>
≥
≤
>0
<0
≥0
≤0
利用不等式的性质解不等式的注意
事项
2.要注意区分“大于” “不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来.
3.在数轴上表示解集应注意的问题:方向、空心圆圈或实心圆点.
1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
例1 某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出V 的取值范围,并在数轴上表示出来.
解:新注入水的体积V与原有水的体积的和不能超过容器的容积,即V+3×5×3≤3×5×10,解得V≤105.又由于新注入水的体积不能是负数,因此,V的取值范围是V≥0并且V≤105.
在数轴上表示V的取值范围如图.
0
105
在表示0和105的点上画实心圆点,表示取值范围包括这两个数.
例2 利用不等式的性质解下列不等式,并在数轴上表示解集:
(1)6x≤5x-7;
解:根据不等式的性质1,不等式两边同时减去5x,不等号方向不变,所以6x-5x≤5x-7-5x,得x≤-7.
在数轴上表示如图所示:
(2)4x≥-12.
解:根据不等式的性质3,不等式两边同时除以4,不等号方向不变,所以x≥-3.
在数轴上表示如图所示:
提示:考虑什么时候需要变号——两边同时除以负数时变号.
A.a≥0 B.a>0 C.a≤0 D.a<0
B
2.莉莉就读的学校上午第一节课的上课时间是8点.莉莉家距学校
有2千米,而她的步行速度为每小时10千米.那么,莉莉上午几点
从家里出发才能保证不迟到?
解:设莉莉上午x点从家里出发才能不迟到,
根据题意得
答:莉莉上午7:48前从家里出发才能不迟到.
≤8,
解得 x≤ .
3.一瓶饮料净重约300 g,瓶上注有“碳水化合物含量≥3%”,其中碳水化合物的含量为多少克?
解:设碳水化合物的含量为x克,根据题意,得 ≥3%,根据不等式的性质2,不等式两边同时乘300,不等号方向不变,所以 ≥3% ×300,x≥9.
答:其中碳水化合物的含量不低于9克.
一个概念:
不等式
两种思想:
数学建模、类比等式
三个注意:
一、要注意“负数”、“非负数”、“不大于”、“不小于”等关键词语的含义;
二、要注意仔细审题,正确列出不等式;
三、要注意观察生活,让数学服务生活.
第九章 不等式与不等式组
9.1.2 不等式的性质(2)
问题 前面学过哪几种形式的不等式?
x
思考 写出下列图片信息中的含义:
问题 铁路部门对随身携带的行李有如下规定:每件行李的长、宽、高之和不得超过160cm.设行李的长、宽、高分别为acm,bcm,ccm,请你列出行李的长、宽、高满足的关系式.
根据题意可得: a+b+c≤160.
我们把用不等号(>,<,≥,≤,≠)连接而成的式子叫作不等式.其中“≥”读作“大于等于”,“≤”读作“小于等于”.
1.不等式的概念
2.常用的表示不等关系的关键词语及对应的不等号
关 键 词 语 第一类:明确表明数量 的不等关系 第二类:明确表明数量的范围特征 ①大 于 ②比…大 ③超 过 ①小 于 ②比…小 ③低 于 ①不小于 ②不低于 ③至 少 ①不大于 ②不超过 ③至 多 正 数 负 数 非 负 数 非
正
数
不 等 号
<
>
≥
≤
>0
<0
≥0
≤0
利用不等式的性质解不等式的注意
事项
2.要注意区分“大于” “不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来.
3.在数轴上表示解集应注意的问题:方向、空心圆圈或实心圆点.
1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
例1 某长方体形状的容器长5cm,宽3cm,高10cm,容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm3)表示新注入水的体积,写出V 的取值范围,并在数轴上表示出来.
解:新注入水的体积V与原有水的体积的和不能超过容器的容积,即V+3×5×3≤3×5×10,解得V≤105.又由于新注入水的体积不能是负数,因此,V的取值范围是V≥0并且V≤105.
在数轴上表示V的取值范围如图.
0
105
在表示0和105的点上画实心圆点,表示取值范围包括这两个数.
例2 利用不等式的性质解下列不等式,并在数轴上表示解集:
(1)6x≤5x-7;
解:根据不等式的性质1,不等式两边同时减去5x,不等号方向不变,所以6x-5x≤5x-7-5x,得x≤-7.
在数轴上表示如图所示:
(2)4x≥-12.
解:根据不等式的性质3,不等式两边同时除以4,不等号方向不变,所以x≥-3.
在数轴上表示如图所示:
提示:考虑什么时候需要变号——两边同时除以负数时变号.
A.a≥0 B.a>0 C.a≤0 D.a<0
B
2.莉莉就读的学校上午第一节课的上课时间是8点.莉莉家距学校
有2千米,而她的步行速度为每小时10千米.那么,莉莉上午几点
从家里出发才能保证不迟到?
解:设莉莉上午x点从家里出发才能不迟到,
根据题意得
答:莉莉上午7:48前从家里出发才能不迟到.
≤8,
解得 x≤ .
3.一瓶饮料净重约300 g,瓶上注有“碳水化合物含量≥3%”,其中碳水化合物的含量为多少克?
解:设碳水化合物的含量为x克,根据题意,得 ≥3%,根据不等式的性质2,不等式两边同时乘300,不等号方向不变,所以 ≥3% ×300,x≥9.
答:其中碳水化合物的含量不低于9克.
一个概念:
不等式
两种思想:
数学建模、类比等式
三个注意:
一、要注意“负数”、“非负数”、“不大于”、“不小于”等关键词语的含义;
二、要注意仔细审题,正确列出不等式;
三、要注意观察生活,让数学服务生活.
