第一单元 第03课时 轴对称图形(教学课件) 四年级数学下册苏教版(共27张PPT)
文档属性
| 名称 | 第一单元 第03课时 轴对称图形(教学课件) 四年级数学下册苏教版(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-24 15:36:27 | ||
图片预览







文档简介
(共27张PPT)
苏教版小学数学四年级下册
轴对称图形
第一单元第三课时
目录
01
情境导入—引“探究”
知识链接—构“联系”
02
新知探究—习“方法”
03
05
作业布置--拓“延伸”
达标练习--活“应用”
04
学习目标
2、认识并掌握确定轴对称图形的对称轴的方法,能画出对称轴;根据对称轴所在的位置,画出轴对称图形的另一半。
1、通过观察、操作、画图等活动,了解轴对称图形的特征。
3、在认识轴对称的过程中,感受与他人合作的乐趣,获得学习成功的愉悦体验,增强对图形变换的兴趣。
学习目标
正确找出轴对称图形对称轴,根据对称轴所在的位置,正确画出轴对称图形的另一半。
找出轴对称图形的所有对称轴。
通过观察、画图等活动进一步认识轴对称,找到对称轴,画出轴对称图形。
核心素养
重 点
难 点
情境引入
还有哪些轴对称图形?
情境引入
知识链接
剪下长方形、正方形和平行四边形。 折一折,哪些是轴对称图形?
知识点小结:如果一个图形沿着一条直线对折后两部分完全重合,那么这样的图形就叫做轴对称图形。
折一折,认识轴对称图形
学习任务一
探求新知
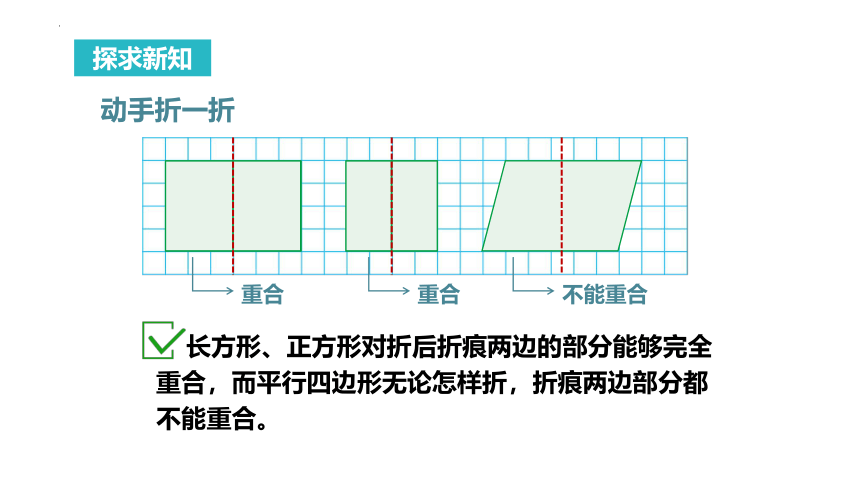
动手折一折
长方形、正方形对折后折痕两边的部分能够完全重合,而平行四边形无论怎样折,折痕两边部分都不能重合。
重合
重合
不能重合
探求新知
长方形是轴对称图形。
正方形是轴对称图形。
平行四边形不是轴对称图形。
找对称轴,补全轴对称图形
学习任务二
探求新知
把长方形纸对折, 使折痕两边完全重合, 有几种不同的折法?
折法一:
把短边对折,将长方形分成两个长不变,宽是原来一半的小长方形。
折痕所在的直线是长方形的对称轴
探求新知
把长方形纸对折, 使折痕两边完全重合, 有几种不同的折法?
折法二:
把长边对折,将长方形分成两个宽不变,长是原来一半的小长方形。
折痕所在的直线也是长方形的对称轴
探求新知
使图形两边完全重合的折痕所在的直线叫作轴对称图形的对称轴。
长方形有两条对称轴。那正方形呢?
探求新知
正方形有几条对称轴?
4条。
折一折,画一画。
对称轴一般用点划线表示;对称轴一般比图形长。
探求新知
易错警示:找不全的对称轴
2条
3条
4条
无数条
有些轴对称图形的对称轴不止一条。
探求新知
把下面的图形补全,使它成为一个轴对称图形。
方法1:在对称轴右边依次画出与左边对称的每一条线段,就可以画出与左边对称的另一半。
方法2:先找到给出的一半图形中的各个顶点,数出每个顶点到对称轴的距离是几格,再在对称轴的另一侧,根据数出的格数找到各个顶点的对称点,然后顺次连接这些点即可。
探求新知
轴对称图形的特征
对折后能重合的一组点叫作对称点。
轴对称图形中相对应的两个点(即对称点)到对称轴的距离相等。
达标练习,巩固成果
学习任务三
达标练习
1. 画出下面图形的对称轴。
课堂练习
达标练习
课堂练习
2. 把下面的图形补全, 使它成为一个轴对称图形。
达标练习
学以致用
3. 根据对称轴画出下面图形的另一半。
达标练习
能力拓展
4. 先画出轴对称图形的另一半,再将整个图形向右平移6格。
达标练习
生活数学
5. 下面是由三个面积相等的小正方形组成的图形,如果再补画一个相同的小正方形,使补画的图形称为轴对称图形,一共有多少种补画的方法?
知识点总结
这节课你有什
么收获?
1.使图形两边完全重合的折痕所在的直线叫作轴对称图形的对称轴。有些轴对称图形的对称轴不止一条。
2.对折后图形两边对应的顶点和边都完全重合。在轴对称图形中,相对应的点到对称轴的距离都相等。
课后作业
1. 认识轴对称图形,掌握轴对称图形特征,并能按要求补画出轴对称图形的另一半;
2. 完成《分层作业》。
启发思维,快乐学习
苏教版小学数学四年级下册
轴对称图形
第一单元第三课时
目录
01
情境导入—引“探究”
知识链接—构“联系”
02
新知探究—习“方法”
03
05
作业布置--拓“延伸”
达标练习--活“应用”
04
学习目标
2、认识并掌握确定轴对称图形的对称轴的方法,能画出对称轴;根据对称轴所在的位置,画出轴对称图形的另一半。
1、通过观察、操作、画图等活动,了解轴对称图形的特征。
3、在认识轴对称的过程中,感受与他人合作的乐趣,获得学习成功的愉悦体验,增强对图形变换的兴趣。
学习目标
正确找出轴对称图形对称轴,根据对称轴所在的位置,正确画出轴对称图形的另一半。
找出轴对称图形的所有对称轴。
通过观察、画图等活动进一步认识轴对称,找到对称轴,画出轴对称图形。
核心素养
重 点
难 点
情境引入
还有哪些轴对称图形?
情境引入
知识链接
剪下长方形、正方形和平行四边形。 折一折,哪些是轴对称图形?
知识点小结:如果一个图形沿着一条直线对折后两部分完全重合,那么这样的图形就叫做轴对称图形。
折一折,认识轴对称图形
学习任务一
探求新知
动手折一折
长方形、正方形对折后折痕两边的部分能够完全重合,而平行四边形无论怎样折,折痕两边部分都不能重合。
重合
重合
不能重合
探求新知
长方形是轴对称图形。
正方形是轴对称图形。
平行四边形不是轴对称图形。
找对称轴,补全轴对称图形
学习任务二
探求新知
把长方形纸对折, 使折痕两边完全重合, 有几种不同的折法?
折法一:
把短边对折,将长方形分成两个长不变,宽是原来一半的小长方形。
折痕所在的直线是长方形的对称轴
探求新知
把长方形纸对折, 使折痕两边完全重合, 有几种不同的折法?
折法二:
把长边对折,将长方形分成两个宽不变,长是原来一半的小长方形。
折痕所在的直线也是长方形的对称轴
探求新知
使图形两边完全重合的折痕所在的直线叫作轴对称图形的对称轴。
长方形有两条对称轴。那正方形呢?
探求新知
正方形有几条对称轴?
4条。
折一折,画一画。
对称轴一般用点划线表示;对称轴一般比图形长。
探求新知
易错警示:找不全的对称轴
2条
3条
4条
无数条
有些轴对称图形的对称轴不止一条。
探求新知
把下面的图形补全,使它成为一个轴对称图形。
方法1:在对称轴右边依次画出与左边对称的每一条线段,就可以画出与左边对称的另一半。
方法2:先找到给出的一半图形中的各个顶点,数出每个顶点到对称轴的距离是几格,再在对称轴的另一侧,根据数出的格数找到各个顶点的对称点,然后顺次连接这些点即可。
探求新知
轴对称图形的特征
对折后能重合的一组点叫作对称点。
轴对称图形中相对应的两个点(即对称点)到对称轴的距离相等。
达标练习,巩固成果
学习任务三
达标练习
1. 画出下面图形的对称轴。
课堂练习
达标练习
课堂练习
2. 把下面的图形补全, 使它成为一个轴对称图形。
达标练习
学以致用
3. 根据对称轴画出下面图形的另一半。
达标练习
能力拓展
4. 先画出轴对称图形的另一半,再将整个图形向右平移6格。
达标练习
生活数学
5. 下面是由三个面积相等的小正方形组成的图形,如果再补画一个相同的小正方形,使补画的图形称为轴对称图形,一共有多少种补画的方法?
知识点总结
这节课你有什
么收获?
1.使图形两边完全重合的折痕所在的直线叫作轴对称图形的对称轴。有些轴对称图形的对称轴不止一条。
2.对折后图形两边对应的顶点和边都完全重合。在轴对称图形中,相对应的点到对称轴的距离都相等。
课后作业
1. 认识轴对称图形,掌握轴对称图形特征,并能按要求补画出轴对称图形的另一半;
2. 完成《分层作业》。
启发思维,快乐学习
