苏教版(2019)高中数学必修第一册 《第8章 函数应用》章末复习 课件(共22张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 《第8章 函数应用》章末复习 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-24 18:40:30 | ||
图片预览








文档简介
(共22张PPT)
苏教版同步教材精品课件
《函数应用》章末复习
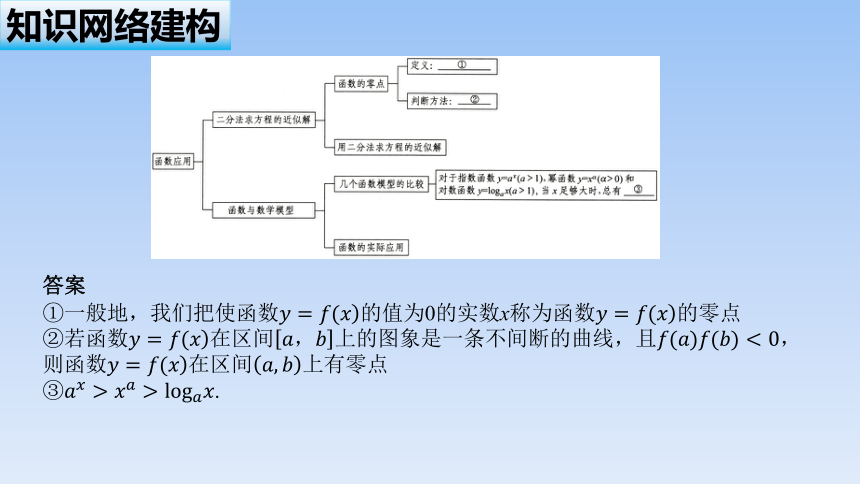
知识网络建构
答案
①一般地,我们把使函数的值为0的实数x称为函数的零点
②若函数在区间上的图象是一条不间断的曲线,且,则函数在区间上有零点
③.
1.确定函数零点的个数有两种基本方法:
一是利用图象研究函数图象与x轴的交点个数或转化为两个函数图象的交点个数定性判断;
二是转化为求相应方程的实数根的个数.
2.函数的零点是一个实数而非一个点,函数的零点就是方程的实数根,也就是函数与的图象交点的横坐标.
3.利用函数零点存在性的判断方法可以判断零点所在的区间,也可以求某些参数的取值范围.
知识要点整合
一、函数的零点
知识要点整合
典例剖析
例1、函数的零点个数为 ( )
A.3 B.2 C.7 D.0
B
解析
方法一:由,得或解得.
因此,函数共有2个零点.
方法二:函数的大致图象如图所示,由图可知,函数共有2个零点.
知识要点整合
典例剖析
例2、已知函数的一个零点在区间上,则实数a的取值范围是( )
A. B. C. D.
解析
因为函数是增函数,且它的一个零点在区间上,所以即
解得,故实数a的取值范围是.
C
用二分法求方程的一个近似解的操作流程是:
知识要点整合
二、用二分法求方程的近似解
知识要点整合
典例剖析
例3、方程的近似解(精确到0.1)是_________.
解析
利用二分法求方程近似解的步骤逐次计算即可.
2.5
1.函数的实际应用主要包含:
(1)利用给定的函数模型解决实际问题;
(2)建立确定性函数模型解决实际问题;
(3)建立拟合函数模型解决实际问题.
上述三个无论是哪一个,所涉及的函数模型主要是:
一(二)次函数模型、指(对)数型函数模型及分段函数模型.
2.建立恰当的函数模型解决实际问题的步骤:
(1)对实际问题进行抽象概括,确定变量之间的关系,并用x,y分别表示;
(2)建立函数模型,将变量y表示为x的函数,此时要注意函数的定义域;
(3)求解函数模型,并还原为实际问题的解.
知识要点整合
三、函数模型及其应用
知识要点整合
典例剖析
例4、为了预防流感,某学校对教室用药熏消毒法进行消毒已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比,药物释放完毕后,y与t的函数关系式为(a为常数),如图所示,根据图中提供的信息,回答下列问题:
解析
(1)药物释放过程中,室内每立方米空气中的含药量y与时间t成正比,设,将代入,得.
同理,将代入,得.综上可知,
(1)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为____________;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过___________小时后,学生才能回到教室.
知识要点整合
典例剖析
例4、为了预防流感,某学校对教室用药熏消毒法进行消毒已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比,药物释放完毕后,y与t的函数关系式为(a为常数),如图所示,根据图中提供的信息,回答下列问题:
解析
(2)令,代入,解得,
从药物释放开始,至少需要0.6小时后,学生才能回到教室.
(1)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为____________;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过___________小时后,学生才能回到教室.
0.6
知识要点整合
典例剖析
例5、某汽车制造商在2018年初公告:随着市场需求量的增加,公司计划2018年生产目标定为43万辆.已知该公司近三年的汽车产量(万辆)如下表所示:
分析
先根据题意求出函数关系式,再通过计算比较得出结论.
如果我们分别将2015,2016,2017,2018定义为第一、二、三、四年.现在你有两个函数模型:二次函数模型,指数型函数模型() ,哪个模型能更好地反映该公司年销量y与年份x的关系?
解析
建立年销量y与年份x的函数,可知函数图象必过点.
(1)构造二次函数模型,
将点的坐标分别代入,可得解得,
则,故,与计划误差为1.
知识要点整合
典例剖析
例5、某汽车制造商在2018年初公告:随着市场需求量的增加,公司计划2018年生产目标定为43万辆.已知该公司近三年的汽车产量(万辆)如下表所示:
如果我们分别将2015,2016,2017,2018定义为第一、二、三、四年.现在你有两个函数模型:二次函数模型,指数型函数模型() ,哪个模型能更好地反映该公司年销量y与年份x的关系?
解析
(2)构造指数型函数模型,将点的坐标代入,可得解得
则,故,与计划误差为1.4.
由(1)(2)可知,二次函数模型能更好地反映该公司年销量y与年份x的关系.
数学运算是解决数学问题的基本手段数学运算是演绎推理,是计算机解决问题的基础.
数学运算主要表现为:理解运算对象,掌握运算法则,探究运算思路,求得运算结果.
本章中,函数零点的判断及求解、二分法求方程的近似解利用函数模型解决实际问题等都体现了数学运算核心素养.
一、数学运算
核心素养梳理
典例剖析
例1、某化工厂生产一种溶液,按市场要求,杂质含量不能超过01%,若初时含杂质2%,每过滤一次可使杂质含量减少,要使产品达到市场要求,则至少应过滤的次数为(已知:) ( )
A.8 B.9
C.10 D.11
解析
根据题意,设需要过滤n次,则,即,
所以,
即.
又,所以,
所以至少应过滤11次才能使产品达到市场要求.
核心素养梳理
B
典例剖析
例2、在天文学中,天体的明暗程度可以用星等或亮度来描述两颗星的星等与亮度满足,其中星等为的星的亮度为.已知太阳的星等是,天狼星的星等是1.45 ,则太阳与天狼星的亮度的比值为 ( )
A. B.10.1 C. D.
解析
令,则,所以,所以.
核心素养梳理
A
数学模型搭建了数学与外部世界联系的桥梁,是数学应用的重要形式数学建模是应用数学解决实际问题的基本手段,也是推动数学发展的动力.
数学建模主要表现为:发现和提出问题,建立和求解模型,检验和完善模型,分析和解决问题.
本章中,建立函数模型解决实际问题体现了数学建模核心素养.
二、数学建模
核心素养梳理
典例剖析
例3、有A,B两种商品,经营销售这两种商品所能获得的利润依次是M(万元)和N(万元),它们与投入资金x(万元)的关系有经验公式:.今有4万元资金投入经营A,B两种商品,为获得最大利润,应分别对A,B两种商品的资金投入多少万元?
分析
先根据题意求出利润关于投入资金的函数关系式,再根据函数的性质求出最大值,即最大利润.
核心素养梳理
设对A种产品投资x万元,则对B种产品投资万元.
于是获得总利润.
由得.
令 ,则.
所以.
解析
典例剖析
例3、有A,B两种商品,经营销售这两种商品所能获得的利润依次是M(万元)和N(万元),它们与投入资金x(万元)的关系有经验公式:.今有4万元资金投入经营A,B两种商品,为获得最大利润,应分别对A,B两种商品的资金投入多少万元?
分析
先根据题意求出利润关于投入资金的函数关系式,再根据函数的性质求出最大值,即最大利润.
核心素养梳理
于是,当时,.
此时,.
故为了获得最大利润,对A种商品的资金投入为1.75万元,对B种商品的资金投入为2.25万元.
解析
函数的零点在高考中的题型以选择题和填空题为主,有时在解答题中也有所涉及,分值一般为5分.高考中对有关函数零点的考查主要有判断函数零点存在的区间、判断函数零点的个数等.
高考真题再现
考点1 函数的零点
典例剖析
例1、(2019·全国Ⅲ)函数在的零点个数为 ( )
A.2 B.3
C.4 D.5
解析
令,则或.又,所以,所以共有3个零点.
高考真题再现
B
例2 、(2014·北京)已知函数,在下列区间中,包含零点的区间是
( )
A. B.
C. D.
解析
包含零点的区间是.
C
函数的实际应用在高考中的题型以填空题和解答题为主,有时在选择题中也有所涉及,分值一般为5~12分.高考中对有关函数实际应用的考查常常以实际生活中的应用问题为背景,设问新颖,重在考查学生的逻辑推理能力,运算求解能力,体现数学建模、数学运算等核心素养.
高考真题再现
考点2 函数的实际应用
典例剖析
例3、(2015·四川)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系(为自然对数的底数,k,b为常数)若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是________小时.
解析
高考真题再现
由题意可得解得该食品在33℃的保鲜时间.
C
苏教版同步教材精品课件
《函数应用》章末复习
知识网络建构
答案
①一般地,我们把使函数的值为0的实数x称为函数的零点
②若函数在区间上的图象是一条不间断的曲线,且,则函数在区间上有零点
③.
1.确定函数零点的个数有两种基本方法:
一是利用图象研究函数图象与x轴的交点个数或转化为两个函数图象的交点个数定性判断;
二是转化为求相应方程的实数根的个数.
2.函数的零点是一个实数而非一个点,函数的零点就是方程的实数根,也就是函数与的图象交点的横坐标.
3.利用函数零点存在性的判断方法可以判断零点所在的区间,也可以求某些参数的取值范围.
知识要点整合
一、函数的零点
知识要点整合
典例剖析
例1、函数的零点个数为 ( )
A.3 B.2 C.7 D.0
B
解析
方法一:由,得或解得.
因此,函数共有2个零点.
方法二:函数的大致图象如图所示,由图可知,函数共有2个零点.
知识要点整合
典例剖析
例2、已知函数的一个零点在区间上,则实数a的取值范围是( )
A. B. C. D.
解析
因为函数是增函数,且它的一个零点在区间上,所以即
解得,故实数a的取值范围是.
C
用二分法求方程的一个近似解的操作流程是:
知识要点整合
二、用二分法求方程的近似解
知识要点整合
典例剖析
例3、方程的近似解(精确到0.1)是_________.
解析
利用二分法求方程近似解的步骤逐次计算即可.
2.5
1.函数的实际应用主要包含:
(1)利用给定的函数模型解决实际问题;
(2)建立确定性函数模型解决实际问题;
(3)建立拟合函数模型解决实际问题.
上述三个无论是哪一个,所涉及的函数模型主要是:
一(二)次函数模型、指(对)数型函数模型及分段函数模型.
2.建立恰当的函数模型解决实际问题的步骤:
(1)对实际问题进行抽象概括,确定变量之间的关系,并用x,y分别表示;
(2)建立函数模型,将变量y表示为x的函数,此时要注意函数的定义域;
(3)求解函数模型,并还原为实际问题的解.
知识要点整合
三、函数模型及其应用
知识要点整合
典例剖析
例4、为了预防流感,某学校对教室用药熏消毒法进行消毒已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比,药物释放完毕后,y与t的函数关系式为(a为常数),如图所示,根据图中提供的信息,回答下列问题:
解析
(1)药物释放过程中,室内每立方米空气中的含药量y与时间t成正比,设,将代入,得.
同理,将代入,得.综上可知,
(1)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为____________;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过___________小时后,学生才能回到教室.
知识要点整合
典例剖析
例4、为了预防流感,某学校对教室用药熏消毒法进行消毒已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比,药物释放完毕后,y与t的函数关系式为(a为常数),如图所示,根据图中提供的信息,回答下列问题:
解析
(2)令,代入,解得,
从药物释放开始,至少需要0.6小时后,学生才能回到教室.
(1)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为____________;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过___________小时后,学生才能回到教室.
0.6
知识要点整合
典例剖析
例5、某汽车制造商在2018年初公告:随着市场需求量的增加,公司计划2018年生产目标定为43万辆.已知该公司近三年的汽车产量(万辆)如下表所示:
分析
先根据题意求出函数关系式,再通过计算比较得出结论.
如果我们分别将2015,2016,2017,2018定义为第一、二、三、四年.现在你有两个函数模型:二次函数模型,指数型函数模型() ,哪个模型能更好地反映该公司年销量y与年份x的关系?
解析
建立年销量y与年份x的函数,可知函数图象必过点.
(1)构造二次函数模型,
将点的坐标分别代入,可得解得,
则,故,与计划误差为1.
知识要点整合
典例剖析
例5、某汽车制造商在2018年初公告:随着市场需求量的增加,公司计划2018年生产目标定为43万辆.已知该公司近三年的汽车产量(万辆)如下表所示:
如果我们分别将2015,2016,2017,2018定义为第一、二、三、四年.现在你有两个函数模型:二次函数模型,指数型函数模型() ,哪个模型能更好地反映该公司年销量y与年份x的关系?
解析
(2)构造指数型函数模型,将点的坐标代入,可得解得
则,故,与计划误差为1.4.
由(1)(2)可知,二次函数模型能更好地反映该公司年销量y与年份x的关系.
数学运算是解决数学问题的基本手段数学运算是演绎推理,是计算机解决问题的基础.
数学运算主要表现为:理解运算对象,掌握运算法则,探究运算思路,求得运算结果.
本章中,函数零点的判断及求解、二分法求方程的近似解利用函数模型解决实际问题等都体现了数学运算核心素养.
一、数学运算
核心素养梳理
典例剖析
例1、某化工厂生产一种溶液,按市场要求,杂质含量不能超过01%,若初时含杂质2%,每过滤一次可使杂质含量减少,要使产品达到市场要求,则至少应过滤的次数为(已知:) ( )
A.8 B.9
C.10 D.11
解析
根据题意,设需要过滤n次,则,即,
所以,
即.
又,所以,
所以至少应过滤11次才能使产品达到市场要求.
核心素养梳理
B
典例剖析
例2、在天文学中,天体的明暗程度可以用星等或亮度来描述两颗星的星等与亮度满足,其中星等为的星的亮度为.已知太阳的星等是,天狼星的星等是1.45 ,则太阳与天狼星的亮度的比值为 ( )
A. B.10.1 C. D.
解析
令,则,所以,所以.
核心素养梳理
A
数学模型搭建了数学与外部世界联系的桥梁,是数学应用的重要形式数学建模是应用数学解决实际问题的基本手段,也是推动数学发展的动力.
数学建模主要表现为:发现和提出问题,建立和求解模型,检验和完善模型,分析和解决问题.
本章中,建立函数模型解决实际问题体现了数学建模核心素养.
二、数学建模
核心素养梳理
典例剖析
例3、有A,B两种商品,经营销售这两种商品所能获得的利润依次是M(万元)和N(万元),它们与投入资金x(万元)的关系有经验公式:.今有4万元资金投入经营A,B两种商品,为获得最大利润,应分别对A,B两种商品的资金投入多少万元?
分析
先根据题意求出利润关于投入资金的函数关系式,再根据函数的性质求出最大值,即最大利润.
核心素养梳理
设对A种产品投资x万元,则对B种产品投资万元.
于是获得总利润.
由得.
令 ,则.
所以.
解析
典例剖析
例3、有A,B两种商品,经营销售这两种商品所能获得的利润依次是M(万元)和N(万元),它们与投入资金x(万元)的关系有经验公式:.今有4万元资金投入经营A,B两种商品,为获得最大利润,应分别对A,B两种商品的资金投入多少万元?
分析
先根据题意求出利润关于投入资金的函数关系式,再根据函数的性质求出最大值,即最大利润.
核心素养梳理
于是,当时,.
此时,.
故为了获得最大利润,对A种商品的资金投入为1.75万元,对B种商品的资金投入为2.25万元.
解析
函数的零点在高考中的题型以选择题和填空题为主,有时在解答题中也有所涉及,分值一般为5分.高考中对有关函数零点的考查主要有判断函数零点存在的区间、判断函数零点的个数等.
高考真题再现
考点1 函数的零点
典例剖析
例1、(2019·全国Ⅲ)函数在的零点个数为 ( )
A.2 B.3
C.4 D.5
解析
令,则或.又,所以,所以共有3个零点.
高考真题再现
B
例2 、(2014·北京)已知函数,在下列区间中,包含零点的区间是
( )
A. B.
C. D.
解析
包含零点的区间是.
C
函数的实际应用在高考中的题型以填空题和解答题为主,有时在选择题中也有所涉及,分值一般为5~12分.高考中对有关函数实际应用的考查常常以实际生活中的应用问题为背景,设问新颖,重在考查学生的逻辑推理能力,运算求解能力,体现数学建模、数学运算等核心素养.
高考真题再现
考点2 函数的实际应用
典例剖析
例3、(2015·四川)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系(为自然对数的底数,k,b为常数)若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是________小时.
解析
高考真题再现
由题意可得解得该食品在33℃的保鲜时间.
C
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
