苏教版(2019)高中数学必修第一册 《第8章 函数的实际应用》专题训练(含解析)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 《第8章 函数的实际应用》专题训练(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-24 00:00:00 | ||
图片预览





文档简介
《函数的实际应用》专题训练
一、选择题
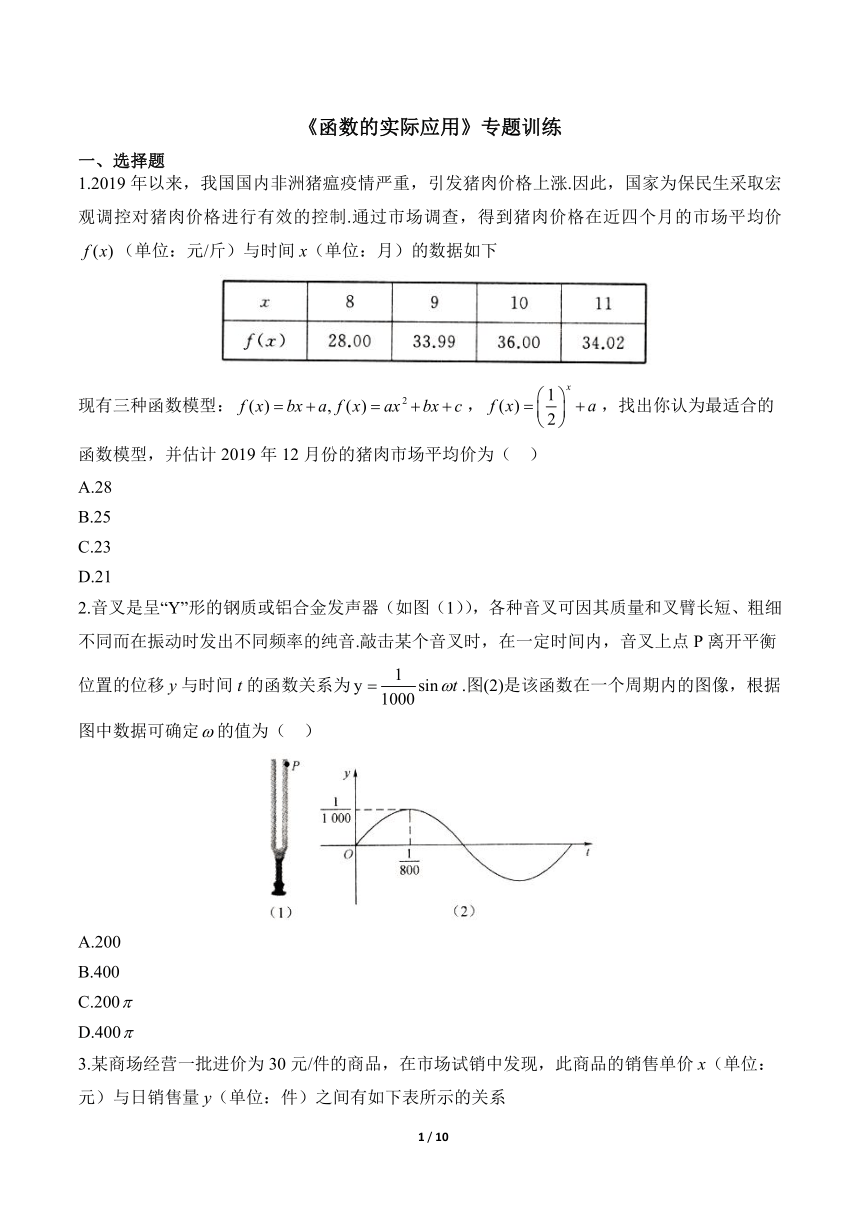
1.2019年以来,我国国内非洲猪瘟疫情严重,引发猪肉价格上涨.因此,国家为保民生采取宏观调控对猪肉价格进行有效的控制.通过市场调查,得到猪肉价格在近四个月的市场平均价(单位:元/斤)与时间x(单位:月)的数据如下
现有三种函数模型:,,找出你认为最适合的函数模型,并估计2019年12月份的猪肉市场平均价为( )
A.28
B.25
C.23
D.21
2.音叉是呈“Y”形的钢质或铝合金发声器(如图(1)),各种音叉可因其质量和叉臂长短、粗细不同而在振动时发出不同频率的纯音.敲击某个音叉时,在一定时间内,音叉上点P离开平衡位置的位移y与时间t的函数关系为.图(2)是该函数在一个周期内的图像,根据图中数据可确定的值为( )
A.200
B.400
C.200
D.400
3.某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如下表所示的关系
设销售单价为x元时,才能获得最大日销售利润p,则x,p分别为( )
A.35,225
B.40,300
C.45,350
D.45,400
4.某企业为激励员工创新,计划逐年加大研发资金投入.若该公司2020年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该企业全年投入的研发资金开始超过200万元的年份是( )
A.2022年
B.2023年
C.2024年
D.2025年
5.某工厂产生的废气必须经过过滤后排放,规定排放时污染物的残留含量不得超过原污染物总量的.已知在过滤过程中的污染物的残留数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为(为常数,为原污染物总量)若前4个小时废气中的污染物被过滤掉了80%,那么要能够按规定排放废气,还需要过滤n小时,则正整数n的最小值为(参考数据:取)( )
A.8
B.9
C.10
D.14
6.惠州市某学校物理兴趣小组在实验测试中收集到一组数据如表所示:
用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( )
A.
B.
C.
D.
二、填空题
7.某餐厅经营盒饭生意,每天的房租、人员工资等固定成本为200元,每盒盒饭的成本为15元,销售单价与日均销售量的关系如下表:
根据以上数据,当这个餐厅每盒盒饭定价 元时,利润最大
8.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,如图(1)所示.假定在水流量稳定的情况下,半径为3m的筒车上的每一个盛水桶都按逆时针方向做角速度为的匀速圆周运动,平面示意图如图(2)所示,已知筒车中心O到水面BC的距离为2m,初始时刻其中一个盛水筒位于点处,且,则8min后该盛水筒到水面的距离为 m.
三、解答题
9.某村电费收取有以下两种方案供农户选择:
方案一:每户每月收取管理费2元,月用电量不超过30度时,每度0.5元;超过30度时,超过部分按每度0.6元收取.
方案二:不收取管理费,每度0.58元.
(1)求方案一的收费(元)与用电量(度)间的函数关系若老王家九月份按方案一缴费35元,问老王家该月用电多少度?
(2)老王家该月用电量在什么范围内,选择方案一比选择方案二好?
10.随着中国经济的快速发展,环保问题已经成为一个不容忽视的问题,而与每个居民的日常生活密切相关的就是水资源问题某污水处理厂在国家环保部门的支持下,引进新设备,污水处理能力大大提高已知该厂每月的污水处理量最少为150万吨,最多为300万吨,月处理成本y(万元)与月处理量x(万吨)之间的函数关系可近似地表示为,且每处理一万吨污水产生的收益价值为0.3万元.
(1)该厂每月污水处理量为多少万吨时,才能使每万吨的处理成本最低?
(2)该厂每月能否获利?如果获利,求出最大利润.
11.进一步改善空气质量,增强人民的蓝天幸福感,2018年7月3日,国务院公开发布《打赢蓝天保卫战三年行动计划》,其中京津冀地区被列为重点治理区域.某课外活动小组根据北京市预报的某天(时)空气质量指数数据绘制成散点图,并选择连续函数来近似刻画空气质量指数y随时间t变化的规律(如图),
(1)求a,b的值;
(2)当空气质量指数大于150时,有关部门建议市民外出活动应戴防雾霾口罩,并禁止某行业施工作业.请你结合该课外活动小组选择的函数模型,回答以下问题:
①某同学该天7:00出发上学,是否应该戴防雾霾口罩?请说明理由;
②试问该天8:00之后,该行业可以施工作业的时间最长为多少小时?
12.某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对,点落在如图所示的两条线段上.该股票在30天内(包括第30天)的日交易量M(万股)与时间t(天)的部分数据如表所示:
(1)根据提供的图像,写出该股票每股交易价格P(元)与时间t(天)所满足的函数关系式P;
(2)根据表中数据,写出日交易量M(万股)与时间t(天)的一次函数关系式;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
参考答案
1.
答案:A
解析:的值随x的值先增后减,选最合适.解得
,代入求得.
2.
答案:D
解析:由y与t的函数关系为,且.
3.
答案:B
解析:由表格可知,x与y满足一次函数关系,设把点和点代入得:解得,
销售利润,
当时,销售利润p的值最大,最大值为300.
4.
答案:C
解析:设第n年开始超过200万元,则130×(1+,
,,
从2024年开始超过200万元.
5.
答案:C
解析:由题意,前4个小时消除了80%的污染物,,,即,,则由,得
,
故正整数n的最小值为.
6.
答案:C
解析:方法一:由表可知,v是关于t的增函数,且增幅随t的增大而增大,故只有C满足要求.
方法二:做出散点图,如下:
由函数拟合可知只有C满足要求.
方法三:由表可知:v是关于t的增函数,故B不适合.对于A,,故A不接近,对于C,,故C接近.
对于D,,故D不接近.
7.
答案:21.5
解析:设销售单价为x元时,销售量为,
日销售利润,
当这个餐厅每盒盒饭定价21.5元时,利润取最大值为1490元.
8.
答案:
解析:由题意知,点离水面的距离的函数为,当时,
,则8min后该盛水筒到水面的距离为m.
9.
答案:见解析
解析:(1)
2 当时,令0.5 +2=35,解得(舍去);
②当 >30时,令,解得,
老王家该月用电60度.
(2)令,
由(1)可得显然为所求.
①时,令,解得;
② >30时,令,解得,则.
综上可得.故当时,选择方案一比选择方案二好.
10.
答案:见解析
解析:(1)由题意可知,每万吨污水的处理成本为,
当且仅当时等号成立.
该厂每月污水处理量为200万吨时,才能使每万吨的处理成本最低,最低成本为万元.
(2)设该厂每月获利为Z万元,则
当时,Z有最大值22.5,
该污水处理厂每月能获利且当月处理量为250万吨时,利润最大,为22.5万元.
11.
答案:见解析
解析:(1)由图像可知,当时,, =11.
又函数为连续函数,.
(2)由(1)可知
①当时,该同学应该戴防雾霾口罩.
②当时,,
令得,,解得10< <22,
该天之后,该行业可以施工作业的时间最长为12个小时.
12.
答案:见解析
解析:(1)当时,设函数解析式为,把点和代入得
解得
.
当时,.
当时,设函数解析式为,
把点和代入得
解得
,
(2)设,
把点和点代入得
解得.
(3)∵该股票每股交易价格日交易量 = +40,
∴该股票日交易额
当时,,当时,
当20 30时,,当时,,
综上所求,在这30天内第15天日交易额最大,最大值为125.
6 / 10
一、选择题
1.2019年以来,我国国内非洲猪瘟疫情严重,引发猪肉价格上涨.因此,国家为保民生采取宏观调控对猪肉价格进行有效的控制.通过市场调查,得到猪肉价格在近四个月的市场平均价(单位:元/斤)与时间x(单位:月)的数据如下
现有三种函数模型:,,找出你认为最适合的函数模型,并估计2019年12月份的猪肉市场平均价为( )
A.28
B.25
C.23
D.21
2.音叉是呈“Y”形的钢质或铝合金发声器(如图(1)),各种音叉可因其质量和叉臂长短、粗细不同而在振动时发出不同频率的纯音.敲击某个音叉时,在一定时间内,音叉上点P离开平衡位置的位移y与时间t的函数关系为.图(2)是该函数在一个周期内的图像,根据图中数据可确定的值为( )
A.200
B.400
C.200
D.400
3.某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x(单位:元)与日销售量y(单位:件)之间有如下表所示的关系
设销售单价为x元时,才能获得最大日销售利润p,则x,p分别为( )
A.35,225
B.40,300
C.45,350
D.45,400
4.某企业为激励员工创新,计划逐年加大研发资金投入.若该公司2020年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该企业全年投入的研发资金开始超过200万元的年份是( )
A.2022年
B.2023年
C.2024年
D.2025年
5.某工厂产生的废气必须经过过滤后排放,规定排放时污染物的残留含量不得超过原污染物总量的.已知在过滤过程中的污染物的残留数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为(为常数,为原污染物总量)若前4个小时废气中的污染物被过滤掉了80%,那么要能够按规定排放废气,还需要过滤n小时,则正整数n的最小值为(参考数据:取)( )
A.8
B.9
C.10
D.14
6.惠州市某学校物理兴趣小组在实验测试中收集到一组数据如表所示:
用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( )
A.
B.
C.
D.
二、填空题
7.某餐厅经营盒饭生意,每天的房租、人员工资等固定成本为200元,每盒盒饭的成本为15元,销售单价与日均销售量的关系如下表:
根据以上数据,当这个餐厅每盒盒饭定价 元时,利润最大
8.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,如图(1)所示.假定在水流量稳定的情况下,半径为3m的筒车上的每一个盛水桶都按逆时针方向做角速度为的匀速圆周运动,平面示意图如图(2)所示,已知筒车中心O到水面BC的距离为2m,初始时刻其中一个盛水筒位于点处,且,则8min后该盛水筒到水面的距离为 m.
三、解答题
9.某村电费收取有以下两种方案供农户选择:
方案一:每户每月收取管理费2元,月用电量不超过30度时,每度0.5元;超过30度时,超过部分按每度0.6元收取.
方案二:不收取管理费,每度0.58元.
(1)求方案一的收费(元)与用电量(度)间的函数关系若老王家九月份按方案一缴费35元,问老王家该月用电多少度?
(2)老王家该月用电量在什么范围内,选择方案一比选择方案二好?
10.随着中国经济的快速发展,环保问题已经成为一个不容忽视的问题,而与每个居民的日常生活密切相关的就是水资源问题某污水处理厂在国家环保部门的支持下,引进新设备,污水处理能力大大提高已知该厂每月的污水处理量最少为150万吨,最多为300万吨,月处理成本y(万元)与月处理量x(万吨)之间的函数关系可近似地表示为,且每处理一万吨污水产生的收益价值为0.3万元.
(1)该厂每月污水处理量为多少万吨时,才能使每万吨的处理成本最低?
(2)该厂每月能否获利?如果获利,求出最大利润.
11.进一步改善空气质量,增强人民的蓝天幸福感,2018年7月3日,国务院公开发布《打赢蓝天保卫战三年行动计划》,其中京津冀地区被列为重点治理区域.某课外活动小组根据北京市预报的某天(时)空气质量指数数据绘制成散点图,并选择连续函数来近似刻画空气质量指数y随时间t变化的规律(如图),
(1)求a,b的值;
(2)当空气质量指数大于150时,有关部门建议市民外出活动应戴防雾霾口罩,并禁止某行业施工作业.请你结合该课外活动小组选择的函数模型,回答以下问题:
①某同学该天7:00出发上学,是否应该戴防雾霾口罩?请说明理由;
②试问该天8:00之后,该行业可以施工作业的时间最长为多少小时?
12.某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对,点落在如图所示的两条线段上.该股票在30天内(包括第30天)的日交易量M(万股)与时间t(天)的部分数据如表所示:
(1)根据提供的图像,写出该股票每股交易价格P(元)与时间t(天)所满足的函数关系式P;
(2)根据表中数据,写出日交易量M(万股)与时间t(天)的一次函数关系式;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
参考答案
1.
答案:A
解析:的值随x的值先增后减,选最合适.解得
,代入求得.
2.
答案:D
解析:由y与t的函数关系为,且.
3.
答案:B
解析:由表格可知,x与y满足一次函数关系,设把点和点代入得:解得,
销售利润,
当时,销售利润p的值最大,最大值为300.
4.
答案:C
解析:设第n年开始超过200万元,则130×(1+,
,,
从2024年开始超过200万元.
5.
答案:C
解析:由题意,前4个小时消除了80%的污染物,,,即,,则由,得
,
故正整数n的最小值为.
6.
答案:C
解析:方法一:由表可知,v是关于t的增函数,且增幅随t的增大而增大,故只有C满足要求.
方法二:做出散点图,如下:
由函数拟合可知只有C满足要求.
方法三:由表可知:v是关于t的增函数,故B不适合.对于A,,故A不接近,对于C,,故C接近.
对于D,,故D不接近.
7.
答案:21.5
解析:设销售单价为x元时,销售量为,
日销售利润,
当这个餐厅每盒盒饭定价21.5元时,利润取最大值为1490元.
8.
答案:
解析:由题意知,点离水面的距离的函数为,当时,
,则8min后该盛水筒到水面的距离为m.
9.
答案:见解析
解析:(1)
2 当时,令0.5 +2=35,解得(舍去);
②当 >30时,令,解得,
老王家该月用电60度.
(2)令,
由(1)可得显然为所求.
①时,令,解得;
② >30时,令,解得,则.
综上可得.故当时,选择方案一比选择方案二好.
10.
答案:见解析
解析:(1)由题意可知,每万吨污水的处理成本为,
当且仅当时等号成立.
该厂每月污水处理量为200万吨时,才能使每万吨的处理成本最低,最低成本为万元.
(2)设该厂每月获利为Z万元,则
当时,Z有最大值22.5,
该污水处理厂每月能获利且当月处理量为250万吨时,利润最大,为22.5万元.
11.
答案:见解析
解析:(1)由图像可知,当时,, =11.
又函数为连续函数,.
(2)由(1)可知
①当时,该同学应该戴防雾霾口罩.
②当时,,
令得,,解得10< <22,
该天之后,该行业可以施工作业的时间最长为12个小时.
12.
答案:见解析
解析:(1)当时,设函数解析式为,把点和代入得
解得
.
当时,.
当时,设函数解析式为,
把点和代入得
解得
,
(2)设,
把点和点代入得
解得.
(3)∵该股票每股交易价格日交易量 = +40,
∴该股票日交易额
当时,,当时,
当20 30时,,当时,,
综上所求,在这30天内第15天日交易额最大,最大值为125.
6 / 10
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
