苏教版(2019)高中数学必修第一册 《第8章 函数应用》单元综合测试B(含解析)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 《第8章 函数应用》单元综合测试B(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-24 18:43:33 | ||
图片预览


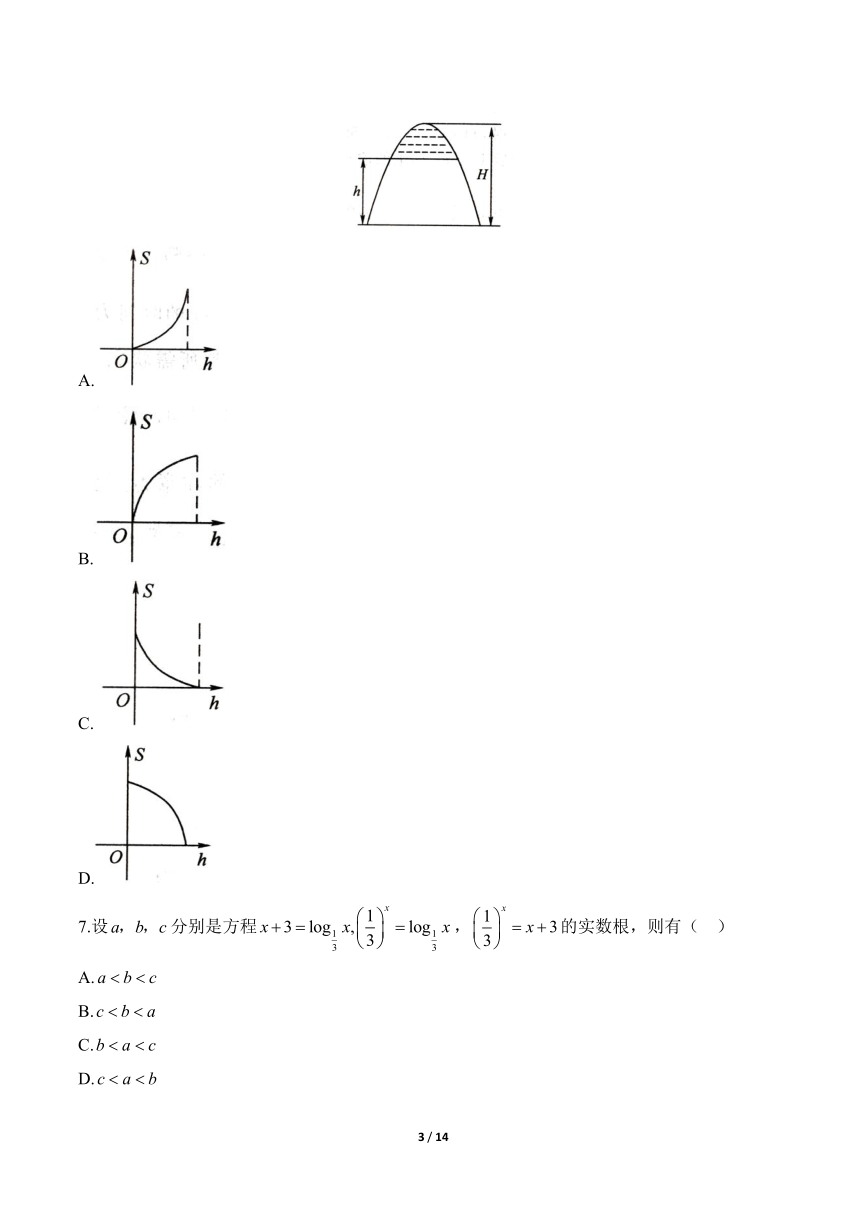


文档简介
《函数应用》单元综合测试B
(时间:120分钟满分:150分)
一、选择题(每小题5分,共60分)
1.函数的零点个数为( )
A.3
B.2
C.1
D.0
2.下列给出的四个函数的图象中,能使函数没有零点的是( )
A.
B.
C.
D.
3.若函数的一个正数零点附近的函数值用二分法计算,其参考数据如下:
那么方程的一个近似解(精确到0.1)可以是( )
A.1.2
B.1.3
C.1.4
D.1.5
4.已知函数,则其零点所在的大致区间为( )
A.
B.
C.
D.
5.如果是函数的零点,且(),那么k的值是( )
A.
B.
C.0
D.1
6.如图所示,阴影部分的面积S是h的函数(),则该函数的图象是下面四个图形中的( )
A.
B.
C.
D.
7.设分别是方程,的实数根,则有( )
A.
B.
C.
D.
8.已知函数,若在区间上存在,使,则实数m的取值范围是( )
A.
B.
C.
D.
9.某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系(为自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在44℃的保鲜时间是( )
A.11小时
B.12小时
C.16小时
D.24小时
10.已知函数的两个零点为,则( )
A.
B.
C.
D.
11.如图,直角梯形OABC中,,直线截此梯形所得位于l左方图形的面积为S,则函数的图象大致为( )
A.
B.
C.
D.
12.函数只有两个零点,则( )
A.
B.
C.
D.
二、填空题(每小题5分,共20分)
13.函数的零点是__________.
14.用二分法求方程在区间(2,4)上的近似解时,取中点,则下一个有解区间是_________.
15.方程在实数范围内的解有__________个.
16.某化工厂生产一种溶液,按市场要求杂质含量不超过01%,若初始时含杂质2%每过滤一次可使杂质含量减少,至少应过滤_________次才能达到市场要求.(已知)
三、解答题(共70分)
17.(10分)设函数(),若函数的图象过点.
(1)求a的值及函数的零点;
(2)求不等式的解集.
18.(12分)设函数的两个零点分别是和2.
(1)求的表达式;
(2)当函数的定义域是时,求函数的值域.
19.(12分)设函数,其中,当时,判断函数在区间上是否存在零点.
20.(12分)某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价x(单位:元/千克)满足关系式,其中,a为常数,已知销售价为6元/千克时,每日可售出该商品220千克.
(1)求a的值;
(2)若该商品的进价为4元/千克,试确定销售价x的值,使商场每日销售该商品所获得的利润最大,并求出利润的最大值.
21.(12分)某公司在2018年承包了一项工程项目,经统计发现该公司在这项工程项目上的月利润P与月份x近似地满足某一函数关系.其中2月到5月所获利润统计如下表:
(1)已知该公司的月利润P与月份x近似满足下列中的某一个函数模型:①;②;③.请以表中该公司这四个月的利润与月份的数据为依据给出你的选择(需要说明选择该模型的理由),并据此估计该公司2018年8月份在这项工程项目中获得的利润;
(2)对(1)中选择的函数模型,若该公司在2018年承包项目的月成本符合函数模型(单位:亿元),求该公司2018年承包的这项工程项目月成本的最大值及相应的月份.
22.(12分)攀枝花是一座资源富集的城市,矿产资源储量巨大,已发现矿种76种,探明储量39种,其中钒、钛资源储量分别占全国的63%和93%,占全球的11%和35%,因此其素有“钒钛之都”的美称攀枝花市某科研单位在研发钛合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值y(y值越大,产品的性能越好)与这种新合金材料的含量x(单位:克)的关系为:当时,y是x的二次函数;当时,测得部分数据如下表:
(1)求y关于x的函数关系式;
(2)该新合金材料的含量x为何值时,产品的性能达到最佳?
参考答案
1.
答案:B
解析:当时,令,则,符合要求;当时,令,则,符合要求,所以的零点有2个.
2.
答案:C
解析:把的图象向下平移1个单位后,只有C中图象与x轴无交点.
3.
答案:C
解析:由表格可知,函数的零点在之间,且1.375与1.4375精确到0.1的近似值均为1.4,所以方程的一个近似解(精确到0.1)是1.4.
4.
答案:C
解析:由题意可知,函数为上的单调增函数,,
,故函数的零点所在的大致区间为.
5.
答案:B
解析:为增函数,,满足,则在上函数存在一个零点,即.又.
6.
答案:C
解析:当时,对应阴影部分的面积小于整个图形面积的一半,且随着h的增大,S随之减小,故排除A,B,D.
7.
答案:D
解析:将方程的实数根问题转化为函数和,和,和图象的交点横坐标问题.
如图,在同一直角坐标系中画出各函数的大致图象,可得.
8.
答案:B
解析:由题意知,,故是单调函数又在区间上存在,使,所以,所以,即,得{ 或解得.
9.
答案:B
解析:由题意可得时,时,,代入,可得,即,则当时,.
10.
答案:A
解析:由题意,作出函数的图象如图所示.不妨设,则,从而,所以,故,所以.
11.
答案:C
解析:由题图可得函数的解析式为
12.
答案:D
解析:令,由题意即要求这两个函数图象有两个交点,利用数形结合思想,作出这两个函数图象可得k的取值范围.
13.
答案:
解析:令,即,解得.故函数的零点是.
14.
答案:
解析:设,则,所以,则下一个有解区间是.
15.
答案:2
解析:可转化为判断函数与的图象的交点个数,如图,有2个交点.
16.
答案:8
解析:设过滤n次才能达到市场要求,则,即,,.又.
17.
答案:见解析
解析:(1)因为函数的图象过点,
所以.
又,且,
所以.
令,则,
即函数的零点为1.
(2),即,变形可得,
解得,即原不等式的解集为.
18.
答案:见解析
解析:(1)函数的两个零点分别是和2,
函数的图象过点,
,①
.②
,得.③
③代入②,得,即.
又.
.
(2),
函数的图象的对称轴是直线,且.
.
函数的值域是.
19.
答案:见解析
解析:因为,
所以.
又,所以,
所以.
又函数的图象在区间上是一条连续曲线,
故函数在区间上存在零点.
20.
答案:见解析
解析:(1)因为,且,
所以,解得.
(2)由(1)知,该商品每日的销售量,
所以商场每日销售该商品所获得的利润
.
因为为二次函数,且其图象的开口向下,对称轴为直线,
所以当时,取得最大值,且最大值为440.
所以当销售价定为6元/千克时,商场每日销售该商品所获得的利润最大,最大利润为440元.
21.
答案:见解析
解析:(1)由题意知.
因为或是单调函数,由所给数据,不具备单调性,故②③不满足条件.
故选择①选择表格中的前三组数据,代入解析式得
即该公司的月利润P与月份x近似满足(且).
当时,(亿元).
即估计该公司2018年8月份在这项工程项目中获得的利润为65亿元.
(2) ,
当时,取得最大值为,即该公司2018年承包的这项工程项目月成本的最大值为11亿元,此时对应的月份是2月.
22.
答案:见解析
解析:(1)当时,y是x的二次函数,可设().
由可得.
由,得.①
由,得.②
由①②解得,
此时.
当时,,由,得,
此时.
综上可得
(2)当时,,
当时,取得最大值12;
当时,递减,可得,当时,取得最大值3.
综上可知,当时产品的性能达到最佳.
1 / 14
(时间:120分钟满分:150分)
一、选择题(每小题5分,共60分)
1.函数的零点个数为( )
A.3
B.2
C.1
D.0
2.下列给出的四个函数的图象中,能使函数没有零点的是( )
A.
B.
C.
D.
3.若函数的一个正数零点附近的函数值用二分法计算,其参考数据如下:
那么方程的一个近似解(精确到0.1)可以是( )
A.1.2
B.1.3
C.1.4
D.1.5
4.已知函数,则其零点所在的大致区间为( )
A.
B.
C.
D.
5.如果是函数的零点,且(),那么k的值是( )
A.
B.
C.0
D.1
6.如图所示,阴影部分的面积S是h的函数(),则该函数的图象是下面四个图形中的( )
A.
B.
C.
D.
7.设分别是方程,的实数根,则有( )
A.
B.
C.
D.
8.已知函数,若在区间上存在,使,则实数m的取值范围是( )
A.
B.
C.
D.
9.某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系(为自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在44℃的保鲜时间是( )
A.11小时
B.12小时
C.16小时
D.24小时
10.已知函数的两个零点为,则( )
A.
B.
C.
D.
11.如图,直角梯形OABC中,,直线截此梯形所得位于l左方图形的面积为S,则函数的图象大致为( )
A.
B.
C.
D.
12.函数只有两个零点,则( )
A.
B.
C.
D.
二、填空题(每小题5分,共20分)
13.函数的零点是__________.
14.用二分法求方程在区间(2,4)上的近似解时,取中点,则下一个有解区间是_________.
15.方程在实数范围内的解有__________个.
16.某化工厂生产一种溶液,按市场要求杂质含量不超过01%,若初始时含杂质2%每过滤一次可使杂质含量减少,至少应过滤_________次才能达到市场要求.(已知)
三、解答题(共70分)
17.(10分)设函数(),若函数的图象过点.
(1)求a的值及函数的零点;
(2)求不等式的解集.
18.(12分)设函数的两个零点分别是和2.
(1)求的表达式;
(2)当函数的定义域是时,求函数的值域.
19.(12分)设函数,其中,当时,判断函数在区间上是否存在零点.
20.(12分)某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价x(单位:元/千克)满足关系式,其中,a为常数,已知销售价为6元/千克时,每日可售出该商品220千克.
(1)求a的值;
(2)若该商品的进价为4元/千克,试确定销售价x的值,使商场每日销售该商品所获得的利润最大,并求出利润的最大值.
21.(12分)某公司在2018年承包了一项工程项目,经统计发现该公司在这项工程项目上的月利润P与月份x近似地满足某一函数关系.其中2月到5月所获利润统计如下表:
(1)已知该公司的月利润P与月份x近似满足下列中的某一个函数模型:①;②;③.请以表中该公司这四个月的利润与月份的数据为依据给出你的选择(需要说明选择该模型的理由),并据此估计该公司2018年8月份在这项工程项目中获得的利润;
(2)对(1)中选择的函数模型,若该公司在2018年承包项目的月成本符合函数模型(单位:亿元),求该公司2018年承包的这项工程项目月成本的最大值及相应的月份.
22.(12分)攀枝花是一座资源富集的城市,矿产资源储量巨大,已发现矿种76种,探明储量39种,其中钒、钛资源储量分别占全国的63%和93%,占全球的11%和35%,因此其素有“钒钛之都”的美称攀枝花市某科研单位在研发钛合金产品的过程中发现了一种新合金材料,由大数据测得该产品的性能指标值y(y值越大,产品的性能越好)与这种新合金材料的含量x(单位:克)的关系为:当时,y是x的二次函数;当时,测得部分数据如下表:
(1)求y关于x的函数关系式;
(2)该新合金材料的含量x为何值时,产品的性能达到最佳?
参考答案
1.
答案:B
解析:当时,令,则,符合要求;当时,令,则,符合要求,所以的零点有2个.
2.
答案:C
解析:把的图象向下平移1个单位后,只有C中图象与x轴无交点.
3.
答案:C
解析:由表格可知,函数的零点在之间,且1.375与1.4375精确到0.1的近似值均为1.4,所以方程的一个近似解(精确到0.1)是1.4.
4.
答案:C
解析:由题意可知,函数为上的单调增函数,,
,故函数的零点所在的大致区间为.
5.
答案:B
解析:为增函数,,满足,则在上函数存在一个零点,即.又.
6.
答案:C
解析:当时,对应阴影部分的面积小于整个图形面积的一半,且随着h的增大,S随之减小,故排除A,B,D.
7.
答案:D
解析:将方程的实数根问题转化为函数和,和,和图象的交点横坐标问题.
如图,在同一直角坐标系中画出各函数的大致图象,可得.
8.
答案:B
解析:由题意知,,故是单调函数又在区间上存在,使,所以,所以,即,得{ 或解得.
9.
答案:B
解析:由题意可得时,时,,代入,可得,即,则当时,.
10.
答案:A
解析:由题意,作出函数的图象如图所示.不妨设,则,从而,所以,故,所以.
11.
答案:C
解析:由题图可得函数的解析式为
12.
答案:D
解析:令,由题意即要求这两个函数图象有两个交点,利用数形结合思想,作出这两个函数图象可得k的取值范围.
13.
答案:
解析:令,即,解得.故函数的零点是.
14.
答案:
解析:设,则,所以,则下一个有解区间是.
15.
答案:2
解析:可转化为判断函数与的图象的交点个数,如图,有2个交点.
16.
答案:8
解析:设过滤n次才能达到市场要求,则,即,,.又.
17.
答案:见解析
解析:(1)因为函数的图象过点,
所以.
又,且,
所以.
令,则,
即函数的零点为1.
(2),即,变形可得,
解得,即原不等式的解集为.
18.
答案:见解析
解析:(1)函数的两个零点分别是和2,
函数的图象过点,
,①
.②
,得.③
③代入②,得,即.
又.
.
(2),
函数的图象的对称轴是直线,且.
.
函数的值域是.
19.
答案:见解析
解析:因为,
所以.
又,所以,
所以.
又函数的图象在区间上是一条连续曲线,
故函数在区间上存在零点.
20.
答案:见解析
解析:(1)因为,且,
所以,解得.
(2)由(1)知,该商品每日的销售量,
所以商场每日销售该商品所获得的利润
.
因为为二次函数,且其图象的开口向下,对称轴为直线,
所以当时,取得最大值,且最大值为440.
所以当销售价定为6元/千克时,商场每日销售该商品所获得的利润最大,最大利润为440元.
21.
答案:见解析
解析:(1)由题意知.
因为或是单调函数,由所给数据,不具备单调性,故②③不满足条件.
故选择①选择表格中的前三组数据,代入解析式得
即该公司的月利润P与月份x近似满足(且).
当时,(亿元).
即估计该公司2018年8月份在这项工程项目中获得的利润为65亿元.
(2) ,
当时,取得最大值为,即该公司2018年承包的这项工程项目月成本的最大值为11亿元,此时对应的月份是2月.
22.
答案:见解析
解析:(1)当时,y是x的二次函数,可设().
由可得.
由,得.①
由,得.②
由①②解得,
此时.
当时,,由,得,
此时.
综上可得
(2)当时,,
当时,取得最大值12;
当时,递减,可得,当时,取得最大值3.
综上可知,当时产品的性能达到最佳.
1 / 14
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
