初中1数学总复习--相似形[上学期]
文档属性
| 名称 | 初中1数学总复习--相似形[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 904.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-29 06:49:00 | ||
图片预览



文档简介
课件19张PPT。 第35课 图形的相似 考试内容:
比例的基本性质,线段的比,成比例线段,图形的相似及性质,三角形相似的条件,图形的位似
考试要求:
(1)了解比例的基本性质,了解线段的比、成比例线段,通过实例了解黄金
分割。
(2)通过实例认识图形的相似,了解相似图形的性质,知道相似多边形的对
应角相等,对应边成比例,面积的比等于对应边比的平方。
(3)了解两个三角形相似的概念,掌握两个三角形相似的条件。
(4)了解图形的位似,能够利用位似将一个图形放大或缩小。
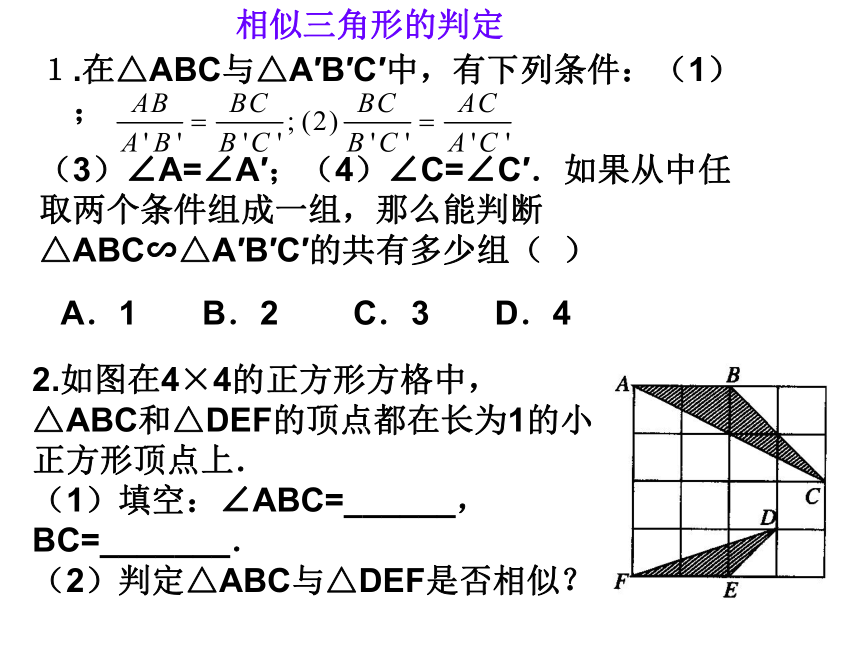
(5)通过实例了解物体的相似,利用图形的相似解决一些实际问题(如利用相似测量旗杆的高度)。1.在△ABC与△A′B′C′中,有下列条件:(1) ;
(3)∠A=∠A′;(4)∠C=∠C′.如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有多少组( ) A.1 B.2 C.3 D.4 2.如图在4×4的正方形方格中,△ABC和△DEF的顶点都在长为1的小正方形顶点上.
(1)填空:∠ABC=______,BC=_______.
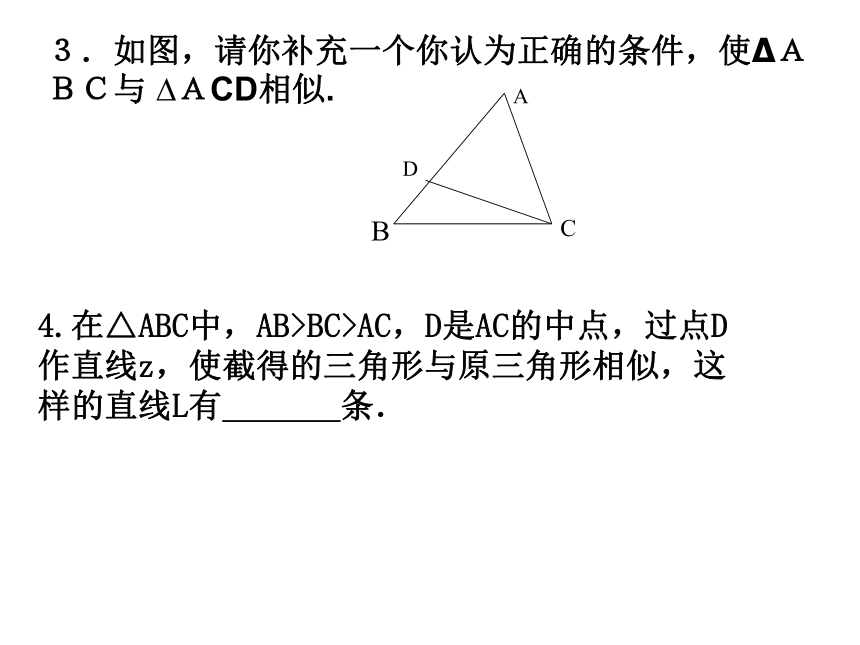
(2)判定△ABC与△DEF是否相似?相似三角形的判定3.如图,请你补充一个你认为正确的条件,使?ABC与 ?ACD相似. 4.在△ABC中,AB>BC>AC,D是AC的中点,过点D作直线z,使截得的三角形与原三角形相似,这样的直线L有 条. 5.如图所示,在△ABC中,AB=AC=1,点D、E在直线BC上运动,设BD=x,CE=y.
(1)如果∠BAC=30°,∠DAE=105°,试确定y与x之间的函数关系式;
(2)如果∠BAC的度数为α,∠DAE的度数为β,当α、β满足怎样的关系式时,(1)中y与x之间的函数关系式还成立,试说明理由.
?
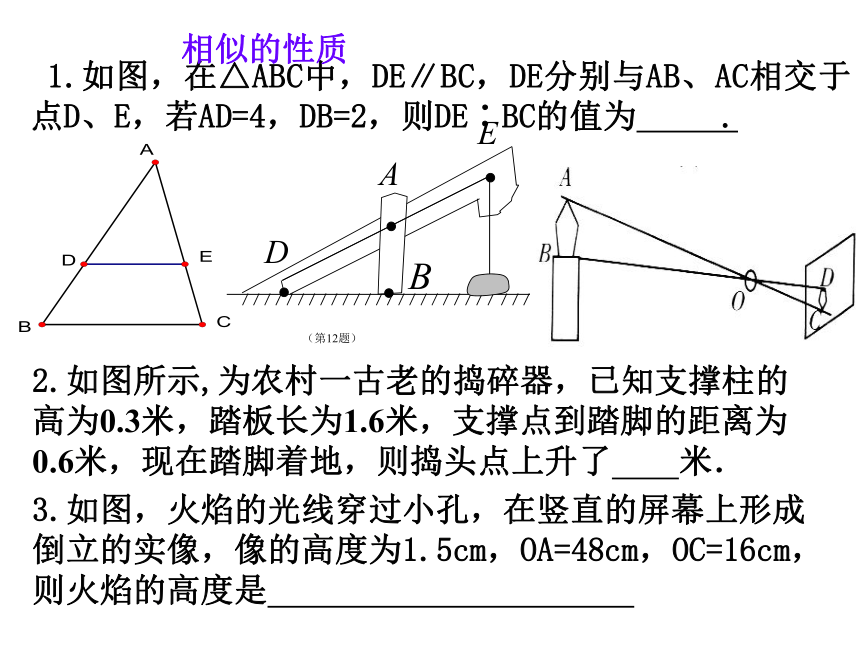
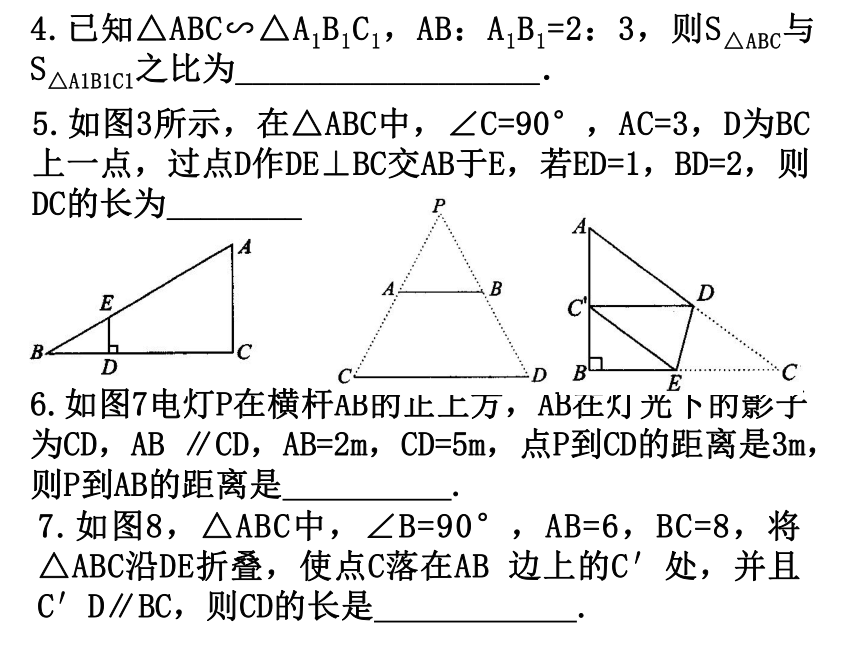
1.如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则DE∶BC的值为 .3.如图,火焰的光线穿过小孔,在竖直的屏幕上形成倒立的实像,像的高度为1.5cm,OA=48cm,OC=16cm,则火焰的高度是 相似的性质 6.如图7电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=5m,点P到CD的距离是3m,则P到AB的距离是 .7.如图8,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的C′处,并且C′D∥BC,则CD的长是 .5.如图3所示,在△ABC中,∠C=90°,AC=3,D为BC上一点,过点D作DE⊥BC交AB于E,若ED=1,BD=2,则DC的长为________4.已知△ABC∽△A1B1C1,AB:A1B1=2:3,则S△ABC与S△A1B1C1之比为__________________.8.9.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少? 10.如图5所示,为了测量一棵树AB的高度,测量者在D点立一高CD=2米的标杆,现测量者从E处可以看到杆顶C与树顶A在同一直线上,如果测得BD=20米,FD=4米,EF=1.8米,则树的高度为__________.11、如图,在长8cm、宽6cm的矩形中,截去一个矩形
(图中阴影部分所示),使留下的矩形与原矩形相似,
那么留下的矩形面积为多少?解:由题意得x 48 = 6 8 ((212.已知两个不相似的直角三角形ABC和A′B′C′中,∠C=∠C′=90°,能否将这两个三角形各分割成两个小三角形,使它们分别相似?你能想出几种分割方法?能否将这个问题推广到有一个角相等的两个任意三角形?13.有一块两直角边长分别为3cm和4cm的直角三角形铁皮,要利用它来裁剪一个正方形,有两种方法:一种是正方形的一边在直角三角形的斜边上,另两个顶点在两条直角边上,如图(1);另一种是一组邻边在直角三角形的两直角边上,另一个顶点在斜边上,如图(2).两种情形下正方形的面积哪个大?为什么?14.如图所示,四边形ABCD为正方形,E是CD的中点,P在BC上,如果BP:PC=1:2,那么请你判:断:△APB和△PCE是否相似,并写出你的理由. 15. 如图,已知
在图(1)中,若 ,则 ;
在图(2)中,若 ,则 ;
在图(3)中,若 ,则 ;
按此规律,若 ,则 . 1.下列说法中不正确的是( )
A.位似图形一定是相似图形;
B.相似图形不一定是位似图形;
C.位似图形上任意一对对应点到位似中心的距离之比等于位似比;
D.位似图形中每组对应点所在的直线必相互平行2.若两个图形位似,则下列叙述不正确的是( )
A.每对对应点所在的直线相交于同一点;
B.两个图形上的对应线段之比等于位似比
C.两个图形上对应线段必平行
D.两个图形的面积比等于位似比的平方位似图形下列说法正确的是( )
A.所有的矩形都是相似形 B.所有的正方形都是相似形C.对应角相等的两个多边形相似
D.对应边成比例的两个多边形相似 A.(-2a,-2b)
B.(-a,-2b)
C.(-2b,-2a)
D.(-2a,-b)某学习小组在讨论“变化的鱼”时,知道大鱼和小鱼是位似图形(如图所示),则小鱼上的点(a,b)对应大鱼上的点.( )3.按如下方法将△ABC的三边缩小来原来的:如图所示,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法中正确的个数是( )
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF是周长的比为2:1; ④△ABC与△DEF面积比为4:1
A.1个 B.2个
C.3个 D.4个4.如图所示,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的位似比为2),画出图形;
(2)分别写出B,C两点的对应点B′,C′的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.5.在矩形ABCD中,已知AB=a,BC=b,P是边CD上异于点C、D的任意一点 .
(1) 若a=2b,当点P在什么位置时,△APB与△BCP相似 (不必证明) ?
(2) 若a≠2b,① 判断以AB为直径的圆与直线CD的位置关系,并说明理由;② 是否存在点P,使以A、B、P为顶点的三角形与以A、D、P为顶点的三角形相似 (不必证明) ?
比例的基本性质,线段的比,成比例线段,图形的相似及性质,三角形相似的条件,图形的位似
考试要求:
(1)了解比例的基本性质,了解线段的比、成比例线段,通过实例了解黄金
分割。
(2)通过实例认识图形的相似,了解相似图形的性质,知道相似多边形的对
应角相等,对应边成比例,面积的比等于对应边比的平方。
(3)了解两个三角形相似的概念,掌握两个三角形相似的条件。
(4)了解图形的位似,能够利用位似将一个图形放大或缩小。
(5)通过实例了解物体的相似,利用图形的相似解决一些实际问题(如利用相似测量旗杆的高度)。1.在△ABC与△A′B′C′中,有下列条件:(1) ;
(3)∠A=∠A′;(4)∠C=∠C′.如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有多少组( ) A.1 B.2 C.3 D.4 2.如图在4×4的正方形方格中,△ABC和△DEF的顶点都在长为1的小正方形顶点上.
(1)填空:∠ABC=______,BC=_______.
(2)判定△ABC与△DEF是否相似?相似三角形的判定3.如图,请你补充一个你认为正确的条件,使?ABC与 ?ACD相似. 4.在△ABC中,AB>BC>AC,D是AC的中点,过点D作直线z,使截得的三角形与原三角形相似,这样的直线L有 条. 5.如图所示,在△ABC中,AB=AC=1,点D、E在直线BC上运动,设BD=x,CE=y.
(1)如果∠BAC=30°,∠DAE=105°,试确定y与x之间的函数关系式;
(2)如果∠BAC的度数为α,∠DAE的度数为β,当α、β满足怎样的关系式时,(1)中y与x之间的函数关系式还成立,试说明理由.
?
1.如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则DE∶BC的值为 .3.如图,火焰的光线穿过小孔,在竖直的屏幕上形成倒立的实像,像的高度为1.5cm,OA=48cm,OC=16cm,则火焰的高度是 相似的性质 6.如图7电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=5m,点P到CD的距离是3m,则P到AB的距离是 .7.如图8,△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的C′处,并且C′D∥BC,则CD的长是 .5.如图3所示,在△ABC中,∠C=90°,AC=3,D为BC上一点,过点D作DE⊥BC交AB于E,若ED=1,BD=2,则DC的长为________4.已知△ABC∽△A1B1C1,AB:A1B1=2:3,则S△ABC与S△A1B1C1之比为__________________.8.9.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少? 10.如图5所示,为了测量一棵树AB的高度,测量者在D点立一高CD=2米的标杆,现测量者从E处可以看到杆顶C与树顶A在同一直线上,如果测得BD=20米,FD=4米,EF=1.8米,则树的高度为__________.11、如图,在长8cm、宽6cm的矩形中,截去一个矩形
(图中阴影部分所示),使留下的矩形与原矩形相似,
那么留下的矩形面积为多少?解:由题意得x 48 = 6 8 ((212.已知两个不相似的直角三角形ABC和A′B′C′中,∠C=∠C′=90°,能否将这两个三角形各分割成两个小三角形,使它们分别相似?你能想出几种分割方法?能否将这个问题推广到有一个角相等的两个任意三角形?13.有一块两直角边长分别为3cm和4cm的直角三角形铁皮,要利用它来裁剪一个正方形,有两种方法:一种是正方形的一边在直角三角形的斜边上,另两个顶点在两条直角边上,如图(1);另一种是一组邻边在直角三角形的两直角边上,另一个顶点在斜边上,如图(2).两种情形下正方形的面积哪个大?为什么?14.如图所示,四边形ABCD为正方形,E是CD的中点,P在BC上,如果BP:PC=1:2,那么请你判:断:△APB和△PCE是否相似,并写出你的理由. 15. 如图,已知
在图(1)中,若 ,则 ;
在图(2)中,若 ,则 ;
在图(3)中,若 ,则 ;
按此规律,若 ,则 . 1.下列说法中不正确的是( )
A.位似图形一定是相似图形;
B.相似图形不一定是位似图形;
C.位似图形上任意一对对应点到位似中心的距离之比等于位似比;
D.位似图形中每组对应点所在的直线必相互平行2.若两个图形位似,则下列叙述不正确的是( )
A.每对对应点所在的直线相交于同一点;
B.两个图形上的对应线段之比等于位似比
C.两个图形上对应线段必平行
D.两个图形的面积比等于位似比的平方位似图形下列说法正确的是( )
A.所有的矩形都是相似形 B.所有的正方形都是相似形C.对应角相等的两个多边形相似
D.对应边成比例的两个多边形相似 A.(-2a,-2b)
B.(-a,-2b)
C.(-2b,-2a)
D.(-2a,-b)某学习小组在讨论“变化的鱼”时,知道大鱼和小鱼是位似图形(如图所示),则小鱼上的点(a,b)对应大鱼上的点.( )3.按如下方法将△ABC的三边缩小来原来的:如图所示,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法中正确的个数是( )
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;③△ABC与△DEF是周长的比为2:1; ④△ABC与△DEF面积比为4:1
A.1个 B.2个
C.3个 D.4个4.如图所示,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的位似比为2),画出图形;
(2)分别写出B,C两点的对应点B′,C′的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.5.在矩形ABCD中,已知AB=a,BC=b,P是边CD上异于点C、D的任意一点 .
(1) 若a=2b,当点P在什么位置时,△APB与△BCP相似 (不必证明) ?
(2) 若a≠2b,① 判断以AB为直径的圆与直线CD的位置关系,并说明理由;② 是否存在点P,使以A、B、P为顶点的三角形与以A、D、P为顶点的三角形相似 (不必证明) ?
