九年级下中考复习解直角三角形[下学期]
文档属性
| 名称 | 九年级下中考复习解直角三角形[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 753.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-18 20:05:00 | ||
图片预览



文档简介
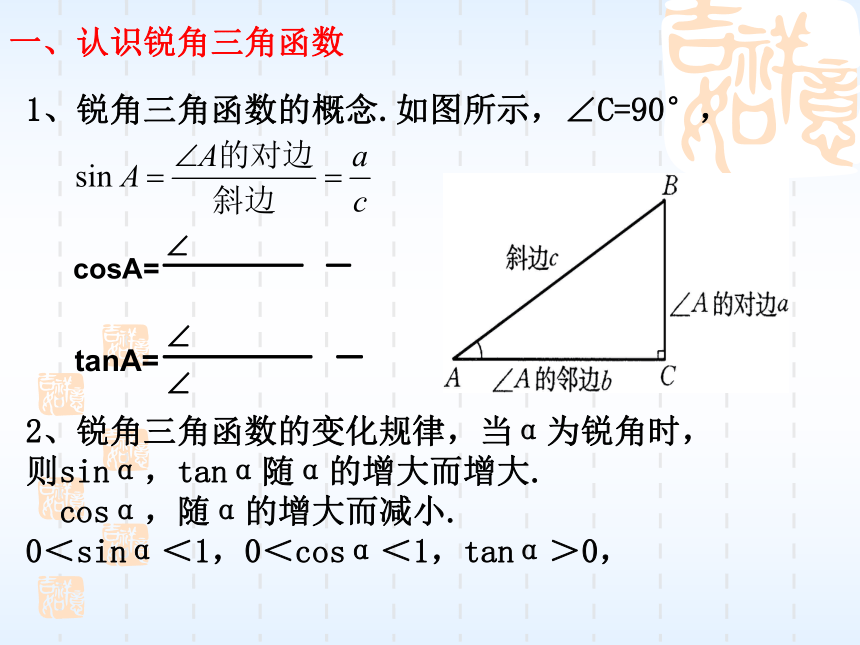
课件30张PPT。解直角三角形 考试说明中对三角函数的要求一、认识锐角三角函数(sinA, cosA, tanA),知道30 °, 45°, 60°角的三角函数值。二、会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角。三、运用三角函数解决与直角三角形有关的简单的实际问题。1、锐角三角函数的概念.如图所示,∠C=90°,
2、锐角三角函数的变化规律,当α为锐角时,
则sinα,tanα随α的增大而增大.
cosα,随α的增大而减小.
0<sinα<1,0<cosα<1,tanα>0,一、认识锐角三角函数
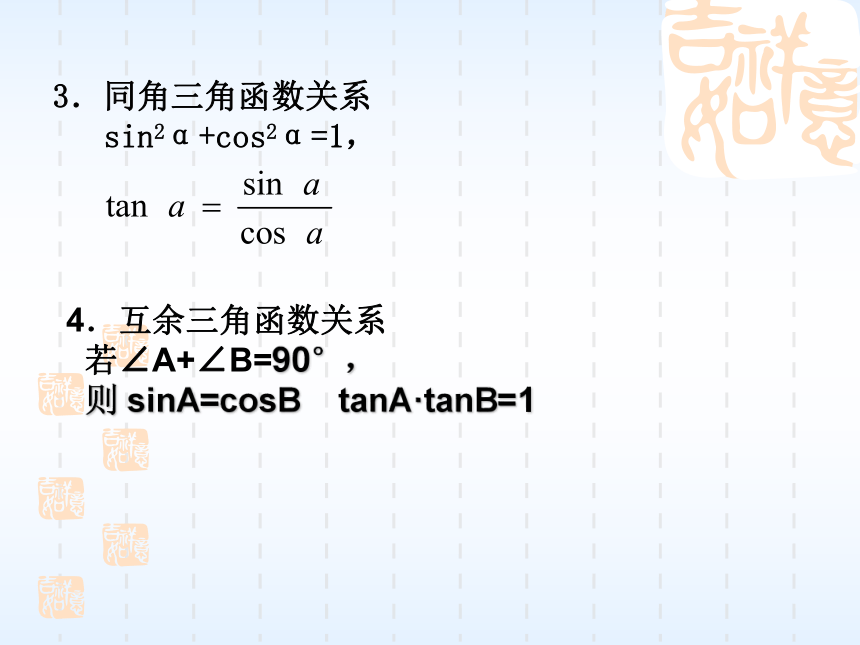
3.同角三角函数关系
sin2α+cos2α=1,
4.互余三角函数关系
若∠A+∠B=90°,
则 sinA=cosB tanA·tanB=1
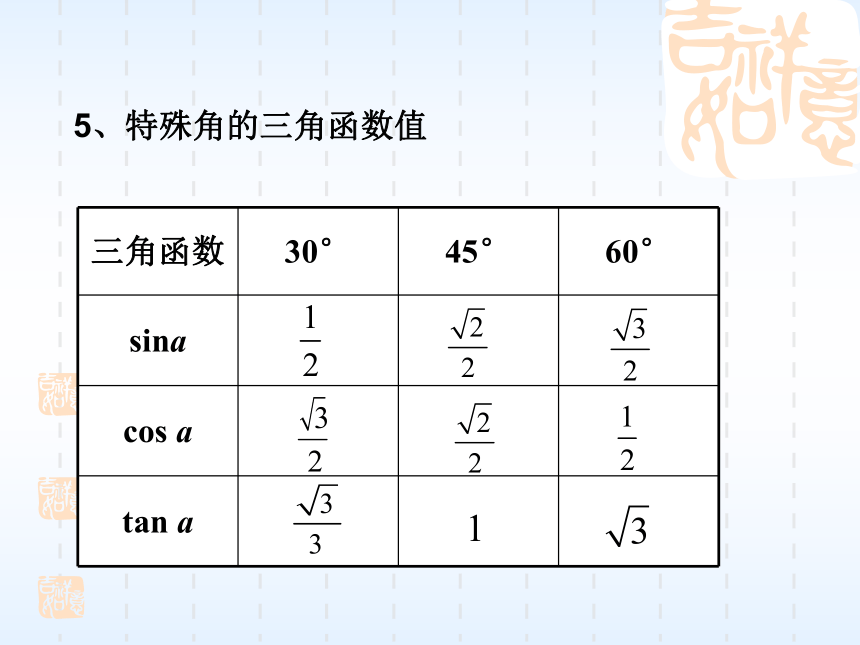
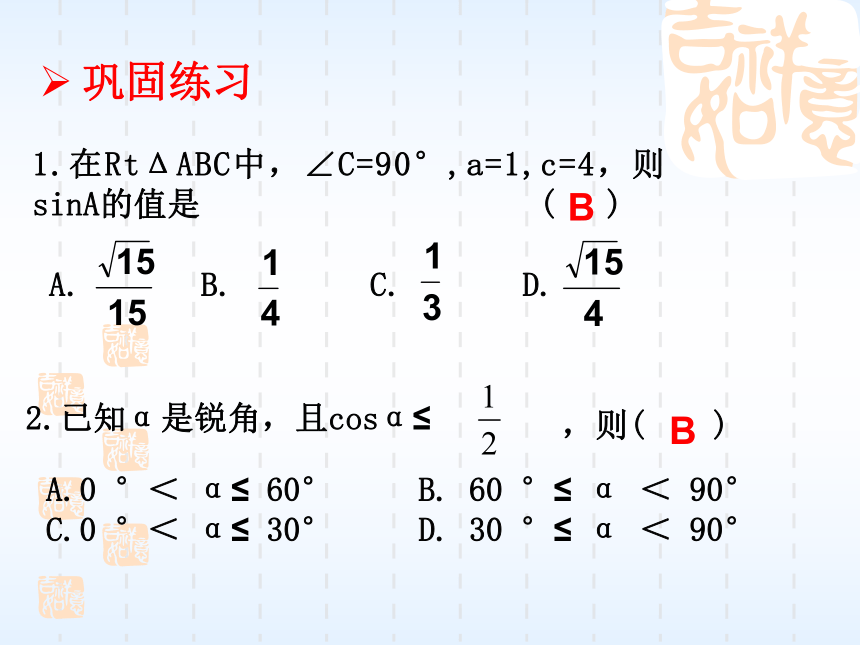
5、特殊角的三角函数值1.在RtΔABC中,∠C=90°,a=1,c=4,则sinA的值是 ( )
A. B. C. D. 2.已知α是锐角,且cosα≤,则( ) A.0 °< α≤ 60° B. 60 °≤ α < 90°
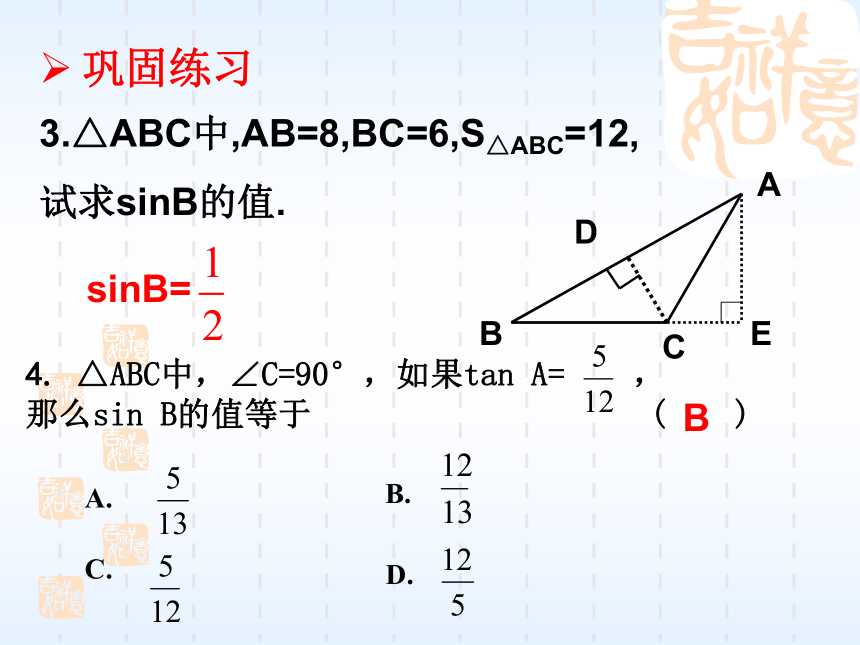
C.0 °< α≤ 30° D. 30 °≤ α < 90°BB巩固练习4. △ABC中,∠C=90°,如果tan A= ,
那么sin B的值等于 ( ) A. B. C. D. B巩固练习3.△ABC中,AB=8,BC=6,S△ABC=12,
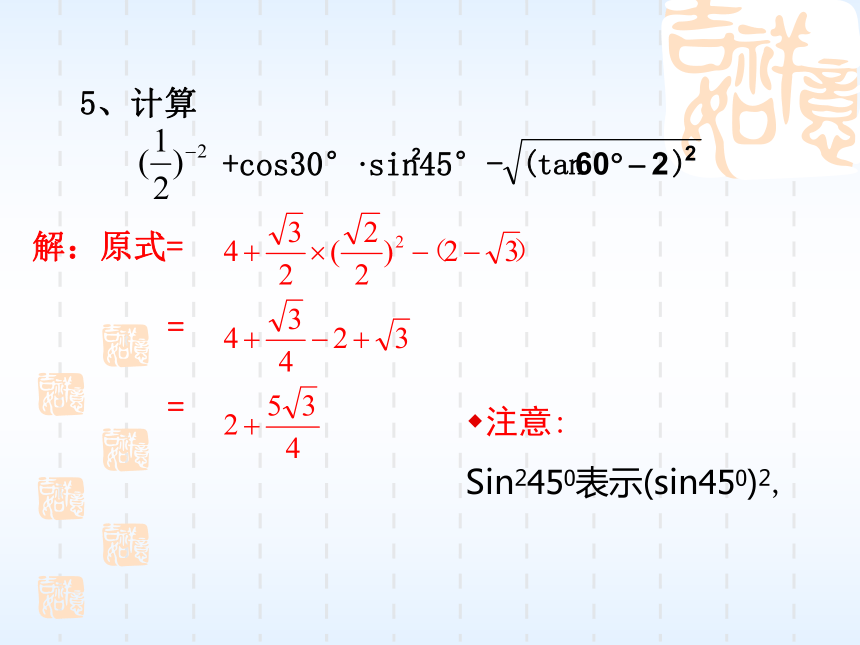
试求sinB的值.ABCDsinB=E5、计算+cos30°·sin45°- 注意:
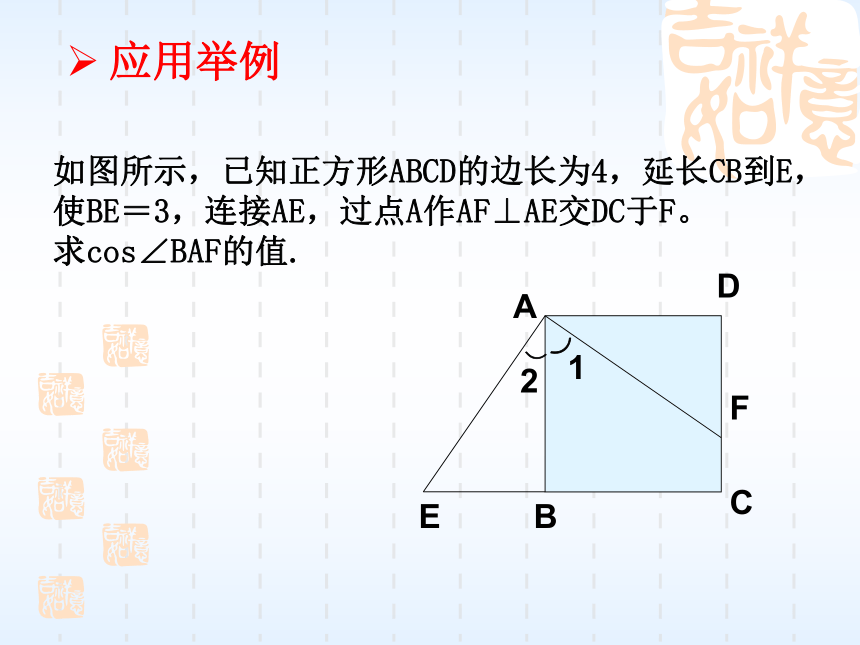
Sin2450表示(sin450)2,2⌒如图所示,已知正方形ABCD的边长为4,延长CB到E,使BE=3,连接AE,过点A作AF⊥AE交DC于F。
求cos∠BAF的值. 应用举例ADCBEF⌒12 要求一个锐角的三角函数值,一定要把这个角构造为直角三角形的一个锐角,再根据定义求.还要熟记特殊角的三角函数值及三角函数公式.
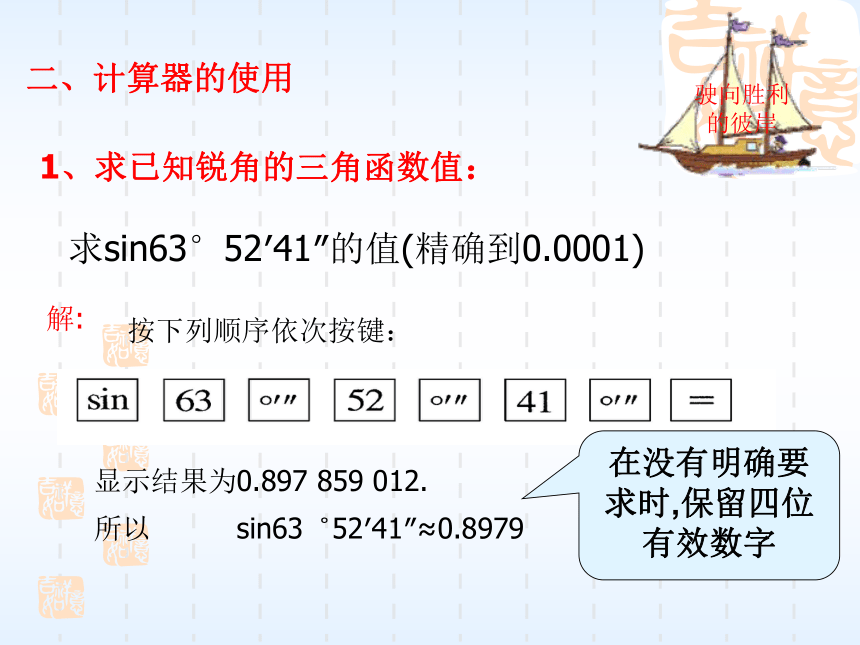
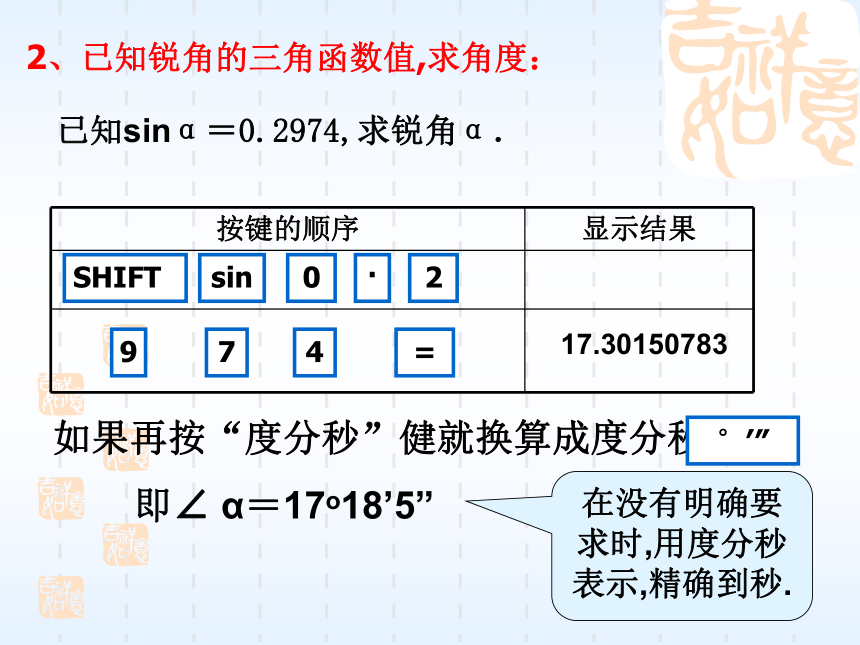
方法小结:1、求已知锐角的三角函数值: 求sin63°52′41″的值(精确到0.0001)解:按下列顺序依次按键:显示结果为0.897 859 012.所以 sin63゜52′41″≈0.8979二、计算器的使用在没有明确要求时,保留四位有效数字SHIFT20917.301507834sin·7=已知sinα=0.2974,求锐角α.
如果再按“度分秒”健就换算成度分秒,°′″即∠ α=17o18’5”2、已知锐角的三角函数值,求角度:在没有明确要求时,用度分秒表示,精确到秒.1、 我军某部在一次野外训练中,有一辆坦克准备通过一座
小山,已知山脚和山顶的水平距离为1000米,山高为565米,
如果这辆坦克能够爬300 的斜坡,试问:它能不能通过这座
小山?巩固练习1.仰角、俯角 在我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的叫做仰角,在水平线
下方的角叫做俯角(如图所示). 三、解直角三角形的应用2.坡度(坡比)、坡角(1)坡度也叫坡比,用i 表示即i = ,
h是坡面的铅直高度,l 为对应水平宽度,
(2)坡角:坡面与水平面的夹角,即∠α.
(3)坡度与坡角(若用α表示)的
关系:i =tanα.3.方向角⌒α 1、某人在A处测得大厦的仰角∠BAC为45度,沿AC方向行20米至D处,测得仰角∠BDC 为60度,求此大厦的高度BC.(精确到米)
BC
A450600D
巩固练习 如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高,精确到米).60°45°A 100米变形题一:BC变形题二:如图,两建筑物的水平距离BD为50米,从点A测得点D的俯角为60度,测得点C的俯角为45度,求AB与CD的高分别是多少?(精确到米)变形题三:
1.把实际问题转化成数学问题,这个转化为两个方面:一是将实际问题的图形转化为几何图形,画出正确的平面或截面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系.2.把数学问题转化成解直角三角形问题,如果示意图不是
直角三角形,可添加适当的辅助线,画出直角三角形.方法小结: “云娜”台风曾给我市造成严重的损失。台风中心从我市(看成一个点A)的正东方向300km的B岛以每时25km的速度正面袭击我市,距台风中心250km的范围内均受台风的影响. 那么影响时间有多长?问题:台风经过我市的路程-------刚好是一个半径为250km的圆的直径解:答:受台风影响的时间
为20小时。 “卡努” 台风中心从我市的正东方向300km处向北偏西60度方向移动,其他数据不变,请问此时,我市会受到台风影响吗?若受影响,则影响的时间又多长?如图,若AD≤250km,则受台风影响;
若AD>250km,则不会受台风影响。 解:会受到影响。以A为圆心,250km长为半径画圆交直线BC于E、F,则DF=DE=200km,答:影响时间为16小时。变形题:1.如图所示,一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时至B处,在B处看见灯塔M在北偏东15°方向,此时灯塔M与渔船的距离是多少? 巩固练习1.如图所示,水坝的横断面是等腰梯形,斜坡AB的坡度i=1∶ ,斜坡AB的水平宽度
BE= m,AD=2m,求∠B,坝高AE及坝底宽BC. 应用举例解:由i=1∶ 可知∠B=30°
又∵BE= ,∴AE=1.
过点D作DF⊥BC于F.
由四边形ABCD为等腰梯形可知FC= 。又∵EF=AD=2,
∴BC=BE+EF+FC= +2+ =2 +2. 1.某山路的坡度i=1: ,沿此山路向上前进200m,则升高了 ( )
A.1m B. m C.2m D.10m2.如图所示,是某市的一块三角形空地,准备在上面种植某种草皮以美化环境,已知这种草皮每平方米售价为a元,则购买这种草皮至少需要( )
A.450a元 B.225a元
C.150a元 D.300a元 DC课时训练 3.如图所示,挂着“庆祝国庆”条幅的氢气球升在广场上空,已知气球的半径为2m,在地面A点测得气球中心O的仰角为60°,测得气球的视角
∠BAC=2°(AB、AC是⊙O的切
线,B、C为切点),则气球
中心O离地面的高度OD为
(sin 1°=0.0175, ,
结果精确到1m) ( )
A.94m B.95m
C.99m D.105mC课时训练
2、锐角三角函数的变化规律,当α为锐角时,
则sinα,tanα随α的增大而增大.
cosα,随α的增大而减小.
0<sinα<1,0<cosα<1,tanα>0,一、认识锐角三角函数
3.同角三角函数关系
sin2α+cos2α=1,
4.互余三角函数关系
若∠A+∠B=90°,
则 sinA=cosB tanA·tanB=1
5、特殊角的三角函数值1.在RtΔABC中,∠C=90°,a=1,c=4,则sinA的值是 ( )
A. B. C. D. 2.已知α是锐角,且cosα≤,则( ) A.0 °< α≤ 60° B. 60 °≤ α < 90°
C.0 °< α≤ 30° D. 30 °≤ α < 90°BB巩固练习4. △ABC中,∠C=90°,如果tan A= ,
那么sin B的值等于 ( ) A. B. C. D. B巩固练习3.△ABC中,AB=8,BC=6,S△ABC=12,
试求sinB的值.ABCDsinB=E5、计算+cos30°·sin45°- 注意:
Sin2450表示(sin450)2,2⌒如图所示,已知正方形ABCD的边长为4,延长CB到E,使BE=3,连接AE,过点A作AF⊥AE交DC于F。
求cos∠BAF的值. 应用举例ADCBEF⌒12 要求一个锐角的三角函数值,一定要把这个角构造为直角三角形的一个锐角,再根据定义求.还要熟记特殊角的三角函数值及三角函数公式.
方法小结:1、求已知锐角的三角函数值: 求sin63°52′41″的值(精确到0.0001)解:按下列顺序依次按键:显示结果为0.897 859 012.所以 sin63゜52′41″≈0.8979二、计算器的使用在没有明确要求时,保留四位有效数字SHIFT20917.301507834sin·7=已知sinα=0.2974,求锐角α.
如果再按“度分秒”健就换算成度分秒,°′″即∠ α=17o18’5”2、已知锐角的三角函数值,求角度:在没有明确要求时,用度分秒表示,精确到秒.1、 我军某部在一次野外训练中,有一辆坦克准备通过一座
小山,已知山脚和山顶的水平距离为1000米,山高为565米,
如果这辆坦克能够爬300 的斜坡,试问:它能不能通过这座
小山?巩固练习1.仰角、俯角 在我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的叫做仰角,在水平线
下方的角叫做俯角(如图所示). 三、解直角三角形的应用2.坡度(坡比)、坡角(1)坡度也叫坡比,用i 表示即i = ,
h是坡面的铅直高度,l 为对应水平宽度,
(2)坡角:坡面与水平面的夹角,即∠α.
(3)坡度与坡角(若用α表示)的
关系:i =tanα.3.方向角⌒α 1、某人在A处测得大厦的仰角∠BAC为45度,沿AC方向行20米至D处,测得仰角∠BDC 为60度,求此大厦的高度BC.(精确到米)
BC
A450600D
巩固练习 如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高,精确到米).60°45°A 100米变形题一:BC变形题二:如图,两建筑物的水平距离BD为50米,从点A测得点D的俯角为60度,测得点C的俯角为45度,求AB与CD的高分别是多少?(精确到米)变形题三:
1.把实际问题转化成数学问题,这个转化为两个方面:一是将实际问题的图形转化为几何图形,画出正确的平面或截面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系.2.把数学问题转化成解直角三角形问题,如果示意图不是
直角三角形,可添加适当的辅助线,画出直角三角形.方法小结: “云娜”台风曾给我市造成严重的损失。台风中心从我市(看成一个点A)的正东方向300km的B岛以每时25km的速度正面袭击我市,距台风中心250km的范围内均受台风的影响. 那么影响时间有多长?问题:台风经过我市的路程-------刚好是一个半径为250km的圆的直径解:答:受台风影响的时间
为20小时。 “卡努” 台风中心从我市的正东方向300km处向北偏西60度方向移动,其他数据不变,请问此时,我市会受到台风影响吗?若受影响,则影响的时间又多长?如图,若AD≤250km,则受台风影响;
若AD>250km,则不会受台风影响。 解:会受到影响。以A为圆心,250km长为半径画圆交直线BC于E、F,则DF=DE=200km,答:影响时间为16小时。变形题:1.如图所示,一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时至B处,在B处看见灯塔M在北偏东15°方向,此时灯塔M与渔船的距离是多少? 巩固练习1.如图所示,水坝的横断面是等腰梯形,斜坡AB的坡度i=1∶ ,斜坡AB的水平宽度
BE= m,AD=2m,求∠B,坝高AE及坝底宽BC. 应用举例解:由i=1∶ 可知∠B=30°
又∵BE= ,∴AE=1.
过点D作DF⊥BC于F.
由四边形ABCD为等腰梯形可知FC= 。又∵EF=AD=2,
∴BC=BE+EF+FC= +2+ =2 +2. 1.某山路的坡度i=1: ,沿此山路向上前进200m,则升高了 ( )
A.1m B. m C.2m D.10m2.如图所示,是某市的一块三角形空地,准备在上面种植某种草皮以美化环境,已知这种草皮每平方米售价为a元,则购买这种草皮至少需要( )
A.450a元 B.225a元
C.150a元 D.300a元 DC课时训练 3.如图所示,挂着“庆祝国庆”条幅的氢气球升在广场上空,已知气球的半径为2m,在地面A点测得气球中心O的仰角为60°,测得气球的视角
∠BAC=2°(AB、AC是⊙O的切
线,B、C为切点),则气球
中心O离地面的高度OD为
(sin 1°=0.0175, ,
结果精确到1m) ( )
A.94m B.95m
C.99m D.105mC课时训练
