中考复习----解直角三角形[下学期]
文档属性
| 名称 | 中考复习----解直角三角形[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-29 00:00:00 | ||
图片预览





文档简介
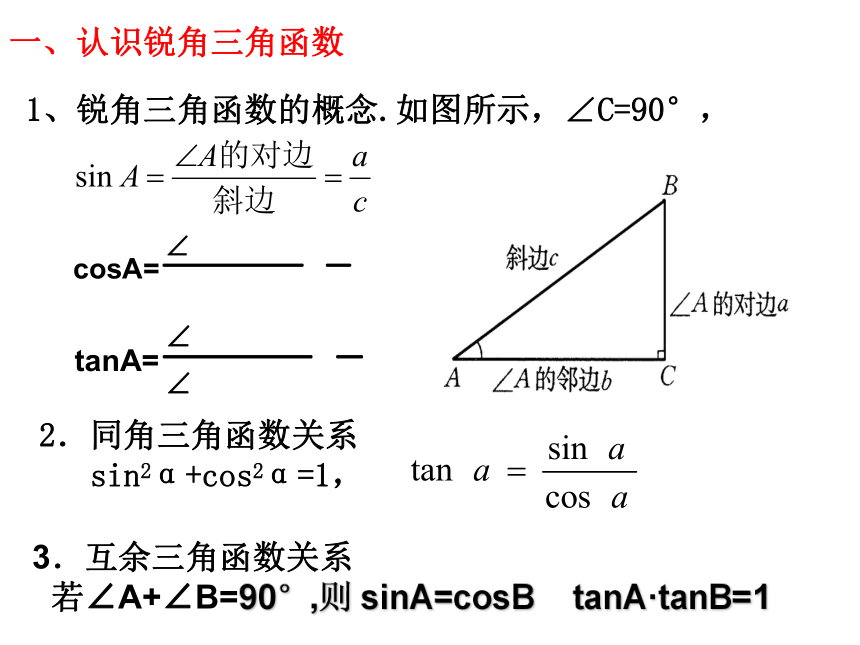
课件20张PPT。2007年中考复习解直角三角形复习一、认识锐角三角函数(sinA, cosA, tanA),知道30 °, 45°, 60°角的三角函数值。二、会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角。三、运用三角函数解决与直角三角形有关的简单的实际问题。中考要求1、锐角三角函数的概念.如图所示,∠C=90°,
一、认识锐角三角函数2.同角三角函数关系
sin2α+cos2α=1,3.互余三角函数关系
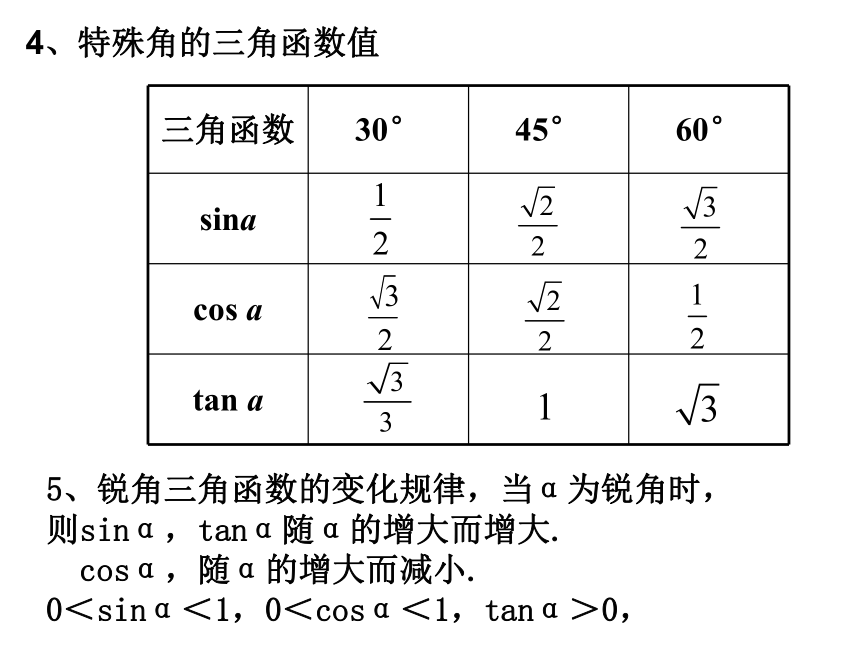
若∠A+∠B=90°,则 sinA=cosB tanA·tanB=1 4、特殊角的三角函数值5、锐角三角函数的变化规律,当α为锐角时,
则sinα,tanα随α的增大而增大.
cosα,随α的增大而减小.
0<sinα<1,0<cosα<1,tanα>0,基础练习1.在RtΔABC中,∠C=90°,a=1,c=4,则sinA的值是 ( )
A. B. C. D.
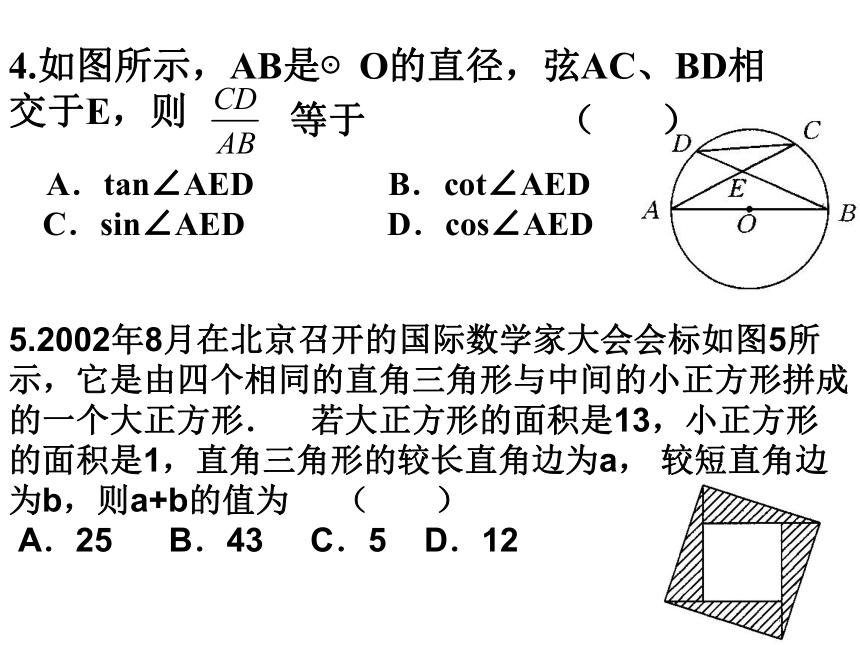
A.tan∠AED B.cot∠AED
C.sin∠AED D.cos∠AED4.如图所示,AB是⊙O的直径,弦AC、BD相交于E,则等于 ( )5.2002年8月在北京召开的国际数学家大会会标如图5所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a, 较短直角边为b,则a+b的值为 ( )
A.25 B.43 C.5 D.12方法小结:
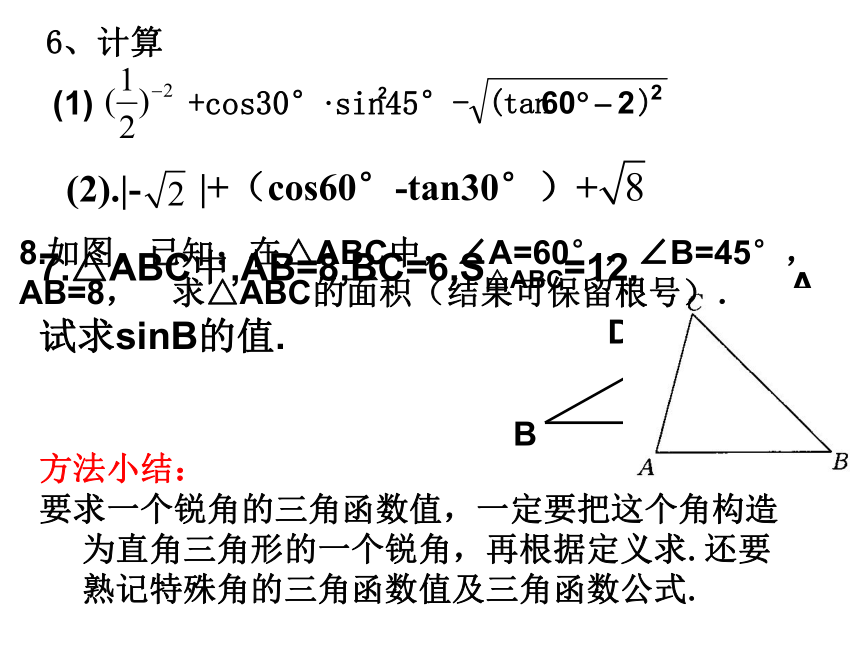
要求一个锐角的三角函数值,一定要把这个角构造为直角三角形的一个锐角,再根据定义求.还要熟记特殊角的三角函数值及三角函数公式. 8.如图,已知:在△ABC中,∠A=60°,∠B=45°,AB=8,求△ABC的面积(结果可保留根号).驶向胜利的彼岸1、求已知锐角的三角函数值: 求sin63°52′41″的值(精确到0.0001)解:按下列顺序依次按键:显示结果为0.897 859 012.所以 sin63゜52′41″≈0.8979二、计算器的使用在没有明确要求时,保留四位有效数字SHIFT20917.301507834sin·7=已知sinα=0.2974,求锐角α.
如果再按“度分秒”健就换算成度分秒,°′″即∠ α=17o18’5”2、已知锐角的三角函数值,求角度:在没有明确要求时,用度分秒表示,精确到秒.1、 我军某部在一次野外训练中,有一辆坦克准备通过一座小山,已知山脚和山顶的水平距离为1000米,山高为565米,如果这辆坦克能够爬300 的斜坡,试问:它能不能通过这座小山?练习在解直角三角形及应用时经常接触到的一些概念(1)仰角和俯角(3)方位角α为坡角三、解直角三角形的应用1.某山路的坡度i=1: ,沿此山路向上前进200m,则升高了 ( )
A.1m B. m C.20m D.10m2.如图所示,是某市的一块三角形空地,准备在上面种植某种草皮以美化环境,已知这种草皮每平方米售价为a元,则购买这种草皮至少需要( )
A.450a元 B.225a元
C.150a元 D.300a元 基础练习 3.如图所示,挂着“庆祝五一”条幅的氢气球升在广场上空,已知气球的半径为2m,在地面A点测得气球中心O的仰角为60°,测得气球的视角∠BAC=2°(AB、AC是⊙O的切线,B、C为切点),则气球中心O离地面的高度OD为(sin 1°=0.0175, ,结果精确到1m) ( )
A.94m B.95m
C.99m D.105m4.如图所示,水坝的横断面是等腰梯形,斜坡AB的坡度i=1∶ ,斜坡AB的水平宽度BE= m,AD=2m,求∠B,坝高AE及坝底宽BC. 基础练习5.如图所示,一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时至B处,在B处看见灯塔M在北偏东15°方向,此时灯塔M与渔船的距离是多少? 体会一下:这节课你有哪些收获?你能否用所学的知识去解决一些
实际问题吗? 1、某人在A处测得大厦的仰角∠BAC为45度,沿AC方向行20米至D处,测得仰角∠BDC 为60度,求此大厦的高度BC.(精确到米) 如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高,精确到米).60°45°A 100米变形题一:BCBD 如图,已知铁塔塔基距房基水平距离BD
为50米,由楼顶A望塔顶的仰角为45 o,由楼顶望塔
底的俯角为30o,塔高DC为 ________米(精确到米) AC变形题二:如图,两建筑物的水平距离BD为50米,从点A测得点D的俯角为60度,测得点C的俯角为45度,求AB与CD的高分别是多少?(精确到米)变形题三:
一、认识锐角三角函数2.同角三角函数关系
sin2α+cos2α=1,3.互余三角函数关系
若∠A+∠B=90°,则 sinA=cosB tanA·tanB=1 4、特殊角的三角函数值5、锐角三角函数的变化规律,当α为锐角时,
则sinα,tanα随α的增大而增大.
cosα,随α的增大而减小.
0<sinα<1,0<cosα<1,tanα>0,基础练习1.在RtΔABC中,∠C=90°,a=1,c=4,则sinA的值是 ( )
A. B. C. D.
A.tan∠AED B.cot∠AED
C.sin∠AED D.cos∠AED4.如图所示,AB是⊙O的直径,弦AC、BD相交于E,则等于 ( )5.2002年8月在北京召开的国际数学家大会会标如图5所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a, 较短直角边为b,则a+b的值为 ( )
A.25 B.43 C.5 D.12方法小结:
要求一个锐角的三角函数值,一定要把这个角构造为直角三角形的一个锐角,再根据定义求.还要熟记特殊角的三角函数值及三角函数公式. 8.如图,已知:在△ABC中,∠A=60°,∠B=45°,AB=8,求△ABC的面积(结果可保留根号).驶向胜利的彼岸1、求已知锐角的三角函数值: 求sin63°52′41″的值(精确到0.0001)解:按下列顺序依次按键:显示结果为0.897 859 012.所以 sin63゜52′41″≈0.8979二、计算器的使用在没有明确要求时,保留四位有效数字SHIFT20917.301507834sin·7=已知sinα=0.2974,求锐角α.
如果再按“度分秒”健就换算成度分秒,°′″即∠ α=17o18’5”2、已知锐角的三角函数值,求角度:在没有明确要求时,用度分秒表示,精确到秒.1、 我军某部在一次野外训练中,有一辆坦克准备通过一座小山,已知山脚和山顶的水平距离为1000米,山高为565米,如果这辆坦克能够爬300 的斜坡,试问:它能不能通过这座小山?练习在解直角三角形及应用时经常接触到的一些概念(1)仰角和俯角(3)方位角α为坡角三、解直角三角形的应用1.某山路的坡度i=1: ,沿此山路向上前进200m,则升高了 ( )
A.1m B. m C.20m D.10m2.如图所示,是某市的一块三角形空地,准备在上面种植某种草皮以美化环境,已知这种草皮每平方米售价为a元,则购买这种草皮至少需要( )
A.450a元 B.225a元
C.150a元 D.300a元 基础练习 3.如图所示,挂着“庆祝五一”条幅的氢气球升在广场上空,已知气球的半径为2m,在地面A点测得气球中心O的仰角为60°,测得气球的视角∠BAC=2°(AB、AC是⊙O的切线,B、C为切点),则气球中心O离地面的高度OD为(sin 1°=0.0175, ,结果精确到1m) ( )
A.94m B.95m
C.99m D.105m4.如图所示,水坝的横断面是等腰梯形,斜坡AB的坡度i=1∶ ,斜坡AB的水平宽度BE= m,AD=2m,求∠B,坝高AE及坝底宽BC. 基础练习5.如图所示,一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时至B处,在B处看见灯塔M在北偏东15°方向,此时灯塔M与渔船的距离是多少? 体会一下:这节课你有哪些收获?你能否用所学的知识去解决一些
实际问题吗? 1、某人在A处测得大厦的仰角∠BAC为45度,沿AC方向行20米至D处,测得仰角∠BDC 为60度,求此大厦的高度BC.(精确到米) 如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度(即求BC边上的高,精确到米).60°45°A 100米变形题一:BCBD 如图,已知铁塔塔基距房基水平距离BD
为50米,由楼顶A望塔顶的仰角为45 o,由楼顶望塔
底的俯角为30o,塔高DC为 ________米(精确到米) AC变形题二:如图,两建筑物的水平距离BD为50米,从点A测得点D的俯角为60度,测得点C的俯角为45度,求AB与CD的高分别是多少?(精确到米)变形题三:
