2023中考数学二轮专题《巧妙建系 解密桥拱——二次函数的应用复习》学案(含答案)
文档属性
| 名称 | 2023中考数学二轮专题《巧妙建系 解密桥拱——二次函数的应用复习》学案(含答案) | 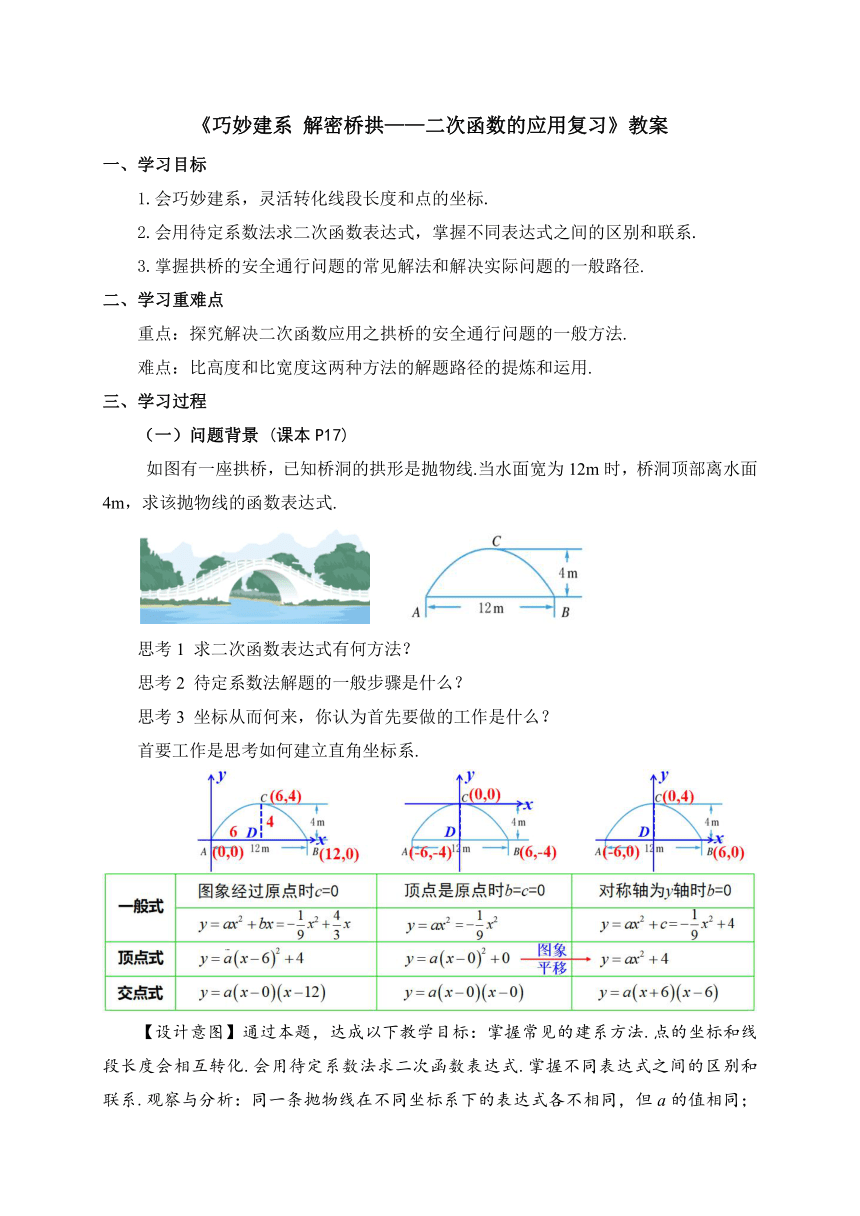 | |
| 格式 | docx | ||
| 文件大小 | 437.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-24 18:37:14 | ||
图片预览

文档简介
《巧妙建系 解密桥拱——二次函数的应用复习》教案
一、学习目标
1.会巧妙建系,灵活转化线段长度和点的坐标.
2.会用待定系数法求二次函数表达式,掌握不同表达式之间的区别和联系.
3.掌握拱桥的安全通行问题的常见解法和解决实际问题的一般路径.
二、学习重难点
重点:探究解决二次函数应用之拱桥的安全通行问题的一般方法.
难点:比高度和比宽度这两种方法的解题路径的提炼和运用.
三、学习过程
(一)问题背景 (课本P17)
如图有一座拱桥,已知桥洞的拱形是抛物线.当水面宽为12m时,桥洞顶部离水面4m,求该抛物线的函数表达式.
思考1 求二次函数表达式有何方法?
思考2 待定系数法解题的一般步骤是什么?
思考3 坐标从而何来,你认为首先要做的工作是什么?
首要工作是思考如何建立直角坐标系.
【设计意图】通过本题,达成以下教学目标:掌握常见的建系方法.点的坐标和线段长度会相互转化.会用待定系数法求二次函数表达式.掌握不同表达式之间的区别和联系.观察与分析:同一条抛物线在不同坐标系下的表达式各不相同,但a的值相同;求表达式的过程难易不同,体会选择建立合适的坐标系的必要性.本环节是后续环节中的解决实际问题的基础,起到铺垫作用.
(二)问题探究
例1.如图,一艘宽2米的船上平放着一些长3米,宽2米,且厚度均匀的长方形
木板,要使该船通过此拱桥,则这些木板最高可堆放到距离水面多少米处?
思考1 船从哪里驶入,才能使木板堆放最高?
思考2 木板怎么放,才能堆放最高?
方法提炼:知x求y得到垂直高度,是求得点的纵坐标的重要依据,为后面学习“比高度”法判断船只能否安全过拱桥做准备.
变式:若已知该拱桥限高米,求可通行船只的最大宽度.
方法提炼:知y求x得到水平宽度,是求得点的横坐标的重要依据,为后面学习“比宽度”法判断船只能否安全过拱桥做准备.
【设计意图】通过问题串的设计,让学生明确船的行驶路线,以及木板的堆放方式,引导学生掌握线段长度与点的坐标之间相互转化.复习了水平线段的长度=x右-x左,竖直线段的长度=y上-y下.通过例1及时提炼出解法:知x求y得到最大高度,为“比高度”作铺垫;通过变式及时提炼出解法:知y求x得到最大宽度,为“比宽度”作铺垫.
(三)拓展生长
例2 现有两艘宽3米,高出水面2米的船只,同时到达该拱桥,它们能在桥下
顺利交汇吗?(不考虑两船间的空隙).
思考1 两船怎样行驶,才可能完成交汇?
思考2 还有其他解法吗?
思考3 哪种方法更简便?
变式:现有两艘宽3米,高出水面2米的船只,同时到达该拱桥,因降暴雨,水位上升1.2米.请问两船能否在桥下顺利交汇?(不考虑两船间的空隙).
思路一:不论水位升降与否,船高出水面的距离保持不变,即MN=2,再比较EN和2的大小。
思路二:水位上涨1.2米,船也跟着升高了1.2米,现在船顶到AB的距离=2+1.2=3.2米,再比较EF和3.2的大小。
【设计意图】情境的生长路线:从一艘船的安全通行问题,拓展到两艘船的安全交汇问题,再拓展生长到水涨船高的安全通行问题.主要复习两种常见的方法:知x求y,然后比高度;知y求x,然后比宽度.
提炼出解决实际问题的一般路径:先通过巧妙建系:以水平方向为x轴,分别以点D、点A、点C为原点,从实际问题中抽象出线段长度,再转化成点的坐标,然后代入二次函数模型求得三个不同的表达式,再代入x求y,然后根据所求的y值去和船高比高度,若最大高度大于船高则船能安全通行,反之.同时,对比不同建系方法中的最优方法,从而突出巧妙建系的重要性.
(四)梳理提升
【设计意图】将本节课的知识建构和方法归纳进行系统地梳理,以思维导图的形式进行呈现,有助于学生思维的成长.
一、学习目标
1.会巧妙建系,灵活转化线段长度和点的坐标.
2.会用待定系数法求二次函数表达式,掌握不同表达式之间的区别和联系.
3.掌握拱桥的安全通行问题的常见解法和解决实际问题的一般路径.
二、学习重难点
重点:探究解决二次函数应用之拱桥的安全通行问题的一般方法.
难点:比高度和比宽度这两种方法的解题路径的提炼和运用.
三、学习过程
(一)问题背景 (课本P17)
如图有一座拱桥,已知桥洞的拱形是抛物线.当水面宽为12m时,桥洞顶部离水面4m,求该抛物线的函数表达式.
思考1 求二次函数表达式有何方法?
思考2 待定系数法解题的一般步骤是什么?
思考3 坐标从而何来,你认为首先要做的工作是什么?
首要工作是思考如何建立直角坐标系.
【设计意图】通过本题,达成以下教学目标:掌握常见的建系方法.点的坐标和线段长度会相互转化.会用待定系数法求二次函数表达式.掌握不同表达式之间的区别和联系.观察与分析:同一条抛物线在不同坐标系下的表达式各不相同,但a的值相同;求表达式的过程难易不同,体会选择建立合适的坐标系的必要性.本环节是后续环节中的解决实际问题的基础,起到铺垫作用.
(二)问题探究
例1.如图,一艘宽2米的船上平放着一些长3米,宽2米,且厚度均匀的长方形
木板,要使该船通过此拱桥,则这些木板最高可堆放到距离水面多少米处?
思考1 船从哪里驶入,才能使木板堆放最高?
思考2 木板怎么放,才能堆放最高?
方法提炼:知x求y得到垂直高度,是求得点的纵坐标的重要依据,为后面学习“比高度”法判断船只能否安全过拱桥做准备.
变式:若已知该拱桥限高米,求可通行船只的最大宽度.
方法提炼:知y求x得到水平宽度,是求得点的横坐标的重要依据,为后面学习“比宽度”法判断船只能否安全过拱桥做准备.
【设计意图】通过问题串的设计,让学生明确船的行驶路线,以及木板的堆放方式,引导学生掌握线段长度与点的坐标之间相互转化.复习了水平线段的长度=x右-x左,竖直线段的长度=y上-y下.通过例1及时提炼出解法:知x求y得到最大高度,为“比高度”作铺垫;通过变式及时提炼出解法:知y求x得到最大宽度,为“比宽度”作铺垫.
(三)拓展生长
例2 现有两艘宽3米,高出水面2米的船只,同时到达该拱桥,它们能在桥下
顺利交汇吗?(不考虑两船间的空隙).
思考1 两船怎样行驶,才可能完成交汇?
思考2 还有其他解法吗?
思考3 哪种方法更简便?
变式:现有两艘宽3米,高出水面2米的船只,同时到达该拱桥,因降暴雨,水位上升1.2米.请问两船能否在桥下顺利交汇?(不考虑两船间的空隙).
思路一:不论水位升降与否,船高出水面的距离保持不变,即MN=2,再比较EN和2的大小。
思路二:水位上涨1.2米,船也跟着升高了1.2米,现在船顶到AB的距离=2+1.2=3.2米,再比较EF和3.2的大小。
【设计意图】情境的生长路线:从一艘船的安全通行问题,拓展到两艘船的安全交汇问题,再拓展生长到水涨船高的安全通行问题.主要复习两种常见的方法:知x求y,然后比高度;知y求x,然后比宽度.
提炼出解决实际问题的一般路径:先通过巧妙建系:以水平方向为x轴,分别以点D、点A、点C为原点,从实际问题中抽象出线段长度,再转化成点的坐标,然后代入二次函数模型求得三个不同的表达式,再代入x求y,然后根据所求的y值去和船高比高度,若最大高度大于船高则船能安全通行,反之.同时,对比不同建系方法中的最优方法,从而突出巧妙建系的重要性.
(四)梳理提升
【设计意图】将本节课的知识建构和方法归纳进行系统地梳理,以思维导图的形式进行呈现,有助于学生思维的成长.
同课章节目录
