苏教版(2019)高中数学选择性必修第一册1.1 直线的斜率与倾斜角【同步精讲】(解析版)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第一册1.1 直线的斜率与倾斜角【同步精讲】(解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 08:54:52 | ||
图片预览




文档简介
第1章 直线与方程
第01讲 直线的斜率与倾斜角
课程标准 重难点
理解直线的斜率和倾斜角的概念;理解直线倾斜角的唯一性及直线斜率的存在性;3.了解斜率公式的推导过程,会应用斜率公式求直线的斜率. 1.倾斜角永远存在但斜率不一定2.倾斜角与斜率的计算
知识点一 直线的倾斜角
在平面直角坐标系中,当直线与轴相交时,我们以轴为基准,轴正向与直线向上的方向之间所成的角叫做直线的倾斜角。
规定:当直线和轴平行或重合时,直线倾斜角为,所以倾斜角的范围是.
【概念解读】
1.要清楚定义中含有的三个条件:①直线向上方向;②轴正向;③小于的角.
2.从运动变化观点来看,直线的倾斜角是由轴按逆时针方向旋转到与直线重合时所成的角.
3.倾斜角的范围是.当时,直线与x轴平行或与x轴重合.
4.直线的倾斜角描述了直线的倾斜程度,每一条直线都有唯一的倾斜角和它对应.
5.已知直线的倾斜角不能确定直线的位置,但是,直线上的一点和这条直线的倾斜角可以唯一确定直线的位置.
知识点二 直线的斜率
斜率的定义
1..倾斜角不是的直线,它的倾斜角的正切叫做这条直线的斜率,常用表示,即.
2.概念解读:当直线与x轴平行或重合时,=0°,k=tan0°=0;直线与x轴垂直时,=90°,k不存在。由此可知,一条直线的倾斜角一定存在,但是斜率k不一定存在.
3.直线的倾斜角与斜率之间的关系
图示
倾斜角(范围) α=0° 0°<α<90° α=90° 90°<α<180°
斜率(范围) k=0 k>0 不存在 k<0
斜率公式
1.斜率公式:已知点、,且与轴不垂直,过两点、的直线的斜率公式.
【概念解读】
对于上面的斜率公式要注意下面五点:
(1) 当x1=x2时,公式右边无意义,直线的斜率不存在,倾斜角=90°,直线与x轴垂直;
(2)k与P1、P2顺序无关,即y1,y2和x1,x2在公式中的前后次序可以同时交换,但分子与分母不能交换;
(3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得;
(4)当y1=y2时,斜率k=0,直线的倾斜角=0°,直线与x轴平行或重合;
(5)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到.
考法01 直线的倾斜角
设直线过原点,其倾斜角为,将直线绕坐标原点沿逆时针方向旋转45°,得到直线,则直线1的倾斜角为
【跟踪训练】
1.已知直线l向上方向与y轴正向所成的角为30°,则直线l的倾斜角为________.
【方法总结】
1.解答此类问题要注意根据倾斜角的概念及倾斜角的取值范围解答.
2.求直线的倾斜角主要根据定义来求,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
考法02 直线的斜率
【例2】如图所示,直线的倾斜角,直线与垂直,求,的斜率.
【跟踪训练】
2.若经过A(m,3),B(1,2)两点的直线的倾斜角为45°,则m=________.
3.经过A(m,3),B(1,2)两点的直线的倾斜角α的取值范围是________(其中m≥1).
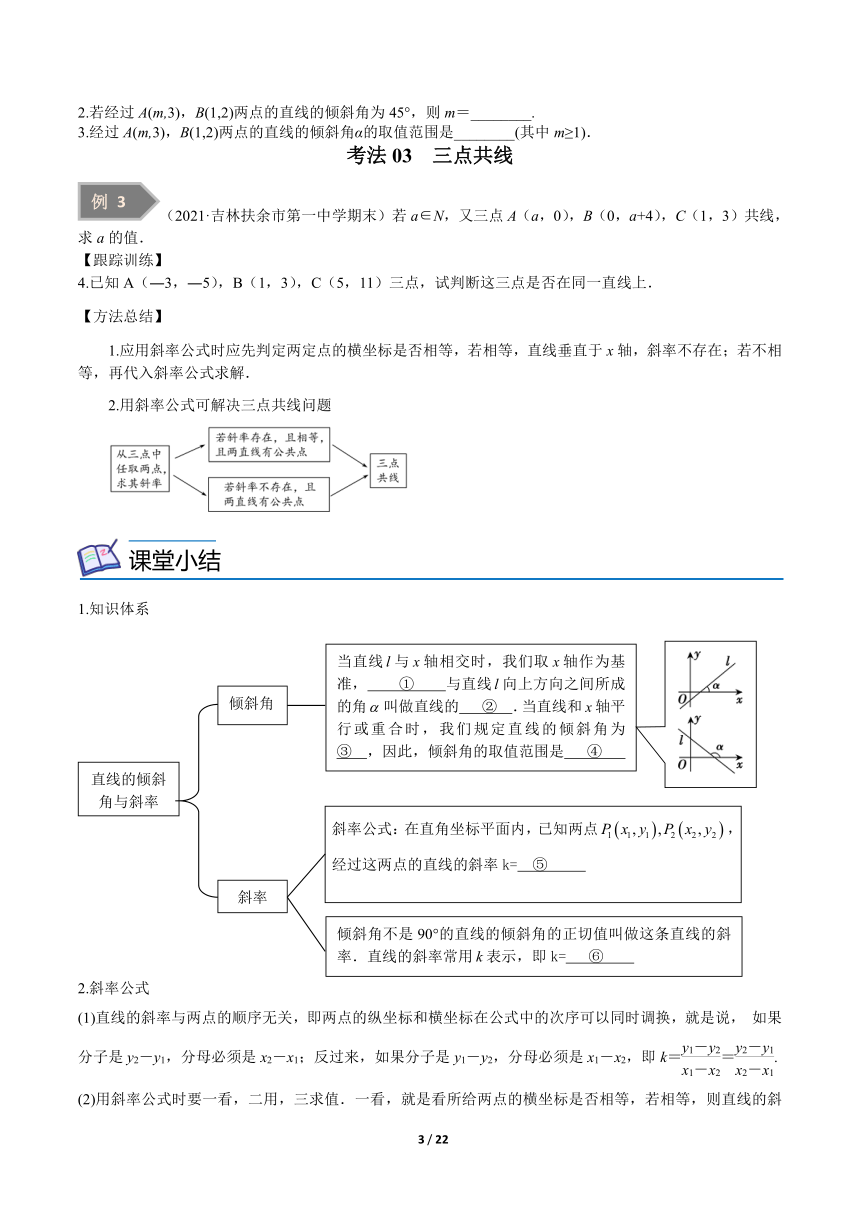
考法03 三点共线
(2021·吉林扶余市第一中学期末)若a∈N,又三点A(a,0),B(0,a+4),C(1,3)共线,求a的值.
【跟踪训练】
4.已知A(―3,―5),B(1,3),C(5,11)三点,试判断这三点是否在同一直线上.
【方法总结】
1.应用斜率公式时应先判定两定点的横坐标是否相等,若相等,直线垂直于x轴,斜率不存在;若不相等,再代入斜率公式求解.
2.用斜率公式可解决三点共线问题
1.知识体系
2.斜率公式
(1)直线的斜率与两点的顺序无关,即两点的纵坐标和横坐标在公式中的次序可以同时调换,就是说, 如果分子是y2-y1,分母必须是x2-x1;反过来,如果分子是y1-y2,分母必须是x1-x2,即k==.
(2)用斜率公式时要一看,二用,三求值.一看,就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第二步;二用,就是将点的坐标代入斜率公式;三求值,就是计算斜率的值,尤其是点的坐标中含有参数时,应用斜率公式时要对参数进行讨论.
题组A 基础过关练
一、单选题
1.直线的倾斜角是( )
A. B. C. D.
2.如图所示,下列四条直线中,斜率最大的是( )
A. B. C. D.
3.如图,在矩形中,,直线的斜率为,则直线的斜率为( )
A. B. C. D.
4.已知正方形的一条对角线所在直线的斜率为,则其一条边所在直线的斜率是( )
A. B. C. D.
5.若,,三点共线,则( )
A. B. C. D.
6.已知点A(1,0),B(2,),C(m,2m),若直线AC的倾斜角是直线AB的倾斜角的2倍,则实数m的值为________.
7.若A(a,0),B(0,b),C(,)三点共线,则________.
8.若直线经过,两点,则直线的倾斜角的大小是________.
题组B 能力提升练
1.直线:与轴交于点,把绕点顺时针旋转得直线,的倾斜角为,则( )
A. B.
C. D.
2.直线xsinα-y+2=0的倾斜角的取值范围是( )
A. B.
C. D.
3.直线的倾斜角的取值范围是( )
A. B. C. D.
4.下列命题中,正确的是( )
A.若直线的倾斜角越大,则直线的斜率就越大
B.若直线的倾斜角为,则直线的斜率为
C.若直线倾斜角,则斜率的取值范围是
D.当直线的倾斜角时,直线的斜率在这个区间上单调递增.
5.已知直线与两点,点,若直线与线段有公共点,则实数的取值范围是______.
6.已知直线的倾斜角为,则的取值范围是_________.
7.已知直线.
(1)若直线过点,试写出直线的一个方向向量;
(2)若实数,求直线的倾斜角的取值范围.
8.已知坐标平面内两点M(m+3,2m+5),N(m-2,1).
(1)当m为何值时,直线MN的倾斜角为锐角?
(2)当m为何值时,直线MN的倾斜角为钝角?
(3)直线MN的倾斜角可能为直角吗?
题组C 培优拔尖练
1.2020年12月4日,嫦娥五号探测器在月球表面第一次动态展示国旗.1949年公布的《国旗制法说明》中就五星的位置规定:大五角星有一个角尖正向上方,四颗小五角星均各有一个角尖正对大五角星的中心点.有人发现,第三颗小星的姿态与大星相近.为便于研究,如图,以大星的中心点为原点,建立直角坐标系,,,,分别是大星中心点与四颗小星中心点的联结线,,则第三颗小星的一条边AB所在直线的倾斜角约为( )
A. B. C. D.
2.坐标平面内有相异两点,,经过两点的直线的的倾斜角的取值范围是( )
A. B.
C. D.
3.已知点,若,则直线AB的倾斜角的取值范围为( )
A. B. C. D.
4.下列说法错误的是( )
A.“”是“直线与直线互相垂直”的充要条件;
B.直线与直线互相平行,则;
C.过两点的所有直线的方程为;
D.经过点且在x轴和y轴上截距都相等的直线方程为.
5.若正方形一条对角线所在直线的斜率为2,则该正方形的两条邻边所在直线的斜率分别为______,_____.
6.颗粒物过滤效率是衡量口罩防护效果的一个重要指标,计算公式为,其中 表示单位体积环境大气中含有的颗粒物数量(单位:),表示经口罩过滤后,单位体积气体中含有的颗粒物数量(单位:).某研究小组在相同的条件下,对两种不同类型口罩的颗粒物过滤效率分别进行了4次测试,测试结果如图所示.图中点的横坐标表示第i种口罩第j次测试时的值,纵坐标表示第i种口罩第j次测试时的值.
该研究小组得到以下结论:
①在第1种口罩的4次测试中,第4次测试时的颗粒物过滤效率最高;
②在第2种口罩的4次测试中,第3次测试时的颗粒物过滤效率最高;
③在每次测试中,第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率高;
④在第3次和第4次测试中,第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率低.
其中,所有正确结论的序号是__________.
(1)与相等的向量共有几个;
(2)与方向相同且模为的向量共有几个;
第1章 直线与方程答案
第01讲 直线的斜率与倾斜角
课程标准 重难点
理解直线的斜率和倾斜角的概念;理解直线倾斜角的唯一性及直线斜率的存在性;3.了解斜率公式的推导过程,会应用斜率公式求直线的斜率. 1.倾斜角永远存在但斜率不一定2.倾斜角与斜率的计算
知识点一 直线的倾斜角
在平面直角坐标系中,当直线与轴相交时,我们以轴为基准,轴正向与直线向上的方向之间所成的角叫做直线的倾斜角。
规定:当直线和轴平行或重合时,直线倾斜角为,所以倾斜角的范围是.
【概念解读】
1.要清楚定义中含有的三个条件:①直线向上方向;②轴正向;③小于的角.
2.从运动变化观点来看,直线的倾斜角是由轴按逆时针方向旋转到与直线重合时所成的角.
3.倾斜角的范围是.当时,直线与x轴平行或与x轴重合.
4.直线的倾斜角描述了直线的倾斜程度,每一条直线都有唯一的倾斜角和它对应.
5.已知直线的倾斜角不能确定直线的位置,但是,直线上的一点和这条直线的倾斜角可以唯一确定直线的位置.
知识点二 直线的斜率
斜率的定义
1..倾斜角不是的直线,它的倾斜角的正切叫做这条直线的斜率,常用表示,即.
2.概念解读:当直线与x轴平行或重合时,=0°,k=tan0°=0;直线与x轴垂直时,=90°,k不存在。由此可知,一条直线的倾斜角一定存在,但是斜率k不一定存在.
3.直线的倾斜角与斜率之间的关系
图示
倾斜角(范围) α=0° 0°<α<90° α=90° 90°<α<180°
斜率(范围) k=0 k>0 不存在 k<0
斜率公式
1.斜率公式:已知点、,且与轴不垂直,过两点、的直线的斜率公式.
【概念解读】
对于上面的斜率公式要注意下面五点:
(1) 当x1=x2时,公式右边无意义,直线的斜率不存在,倾斜角=90°,直线与x轴垂直;
(2)k与P1、P2顺序无关,即y1,y2和x1,x2在公式中的前后次序可以同时交换,但分子与分母不能交换;
(3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得;
(4)当y1=y2时,斜率k=0,直线的倾斜角=0°,直线与x轴平行或重合;
(5)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到.
考法01 直线的倾斜角
设直线过原点,其倾斜角为,将直线绕坐标原点沿逆时针方向旋转45°,得到直线,则直线1的倾斜角为
【答案】当0°≤<135°时,为+45°,当135°≤<180°时,为-135°
【解析】倾斜角的范围是[0°,180°),因此,只有当+45°∈[0°,180°),即当0°≤<135°时,的倾斜角才是+45°,而当135°≤<180°时,的倾斜角为-135°.故应选D.
【跟踪训练】
1.已知直线l向上方向与y轴正向所成的角为30°,则直线l的倾斜角为________.
【答案】60°或120°
【解析】有两种情况:①如图(1),直线l向上方向与x轴正向所成的角为60°,即直线l的倾斜角为60°.
②如图(2),直线l向上方向与x轴正向所成的角为120°,即直线l的倾斜角为120°.
【方法总结】
1.解答此类问题要注意根据倾斜角的概念及倾斜角的取值范围解答.
2.求直线的倾斜角主要根据定义来求,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
考法02 直线的斜率
【例2】如图所示,直线的倾斜角,直线与垂直,求,的斜率.
【解析】由图形可知,,则k1,k2可求.
直线的斜率.
∵直线的倾斜角=90°+30°=120°,
∴直线的斜率k2=tan120°=tan(180°―60°)=―tan60°=.
【跟踪训练】
2.若经过A(m,3),B(1,2)两点的直线的倾斜角为45°,则m=________.
【答案】1.2
【解析】tan 45°=,得m=2.
3.经过A(m,3),B(1,2)两点的直线的倾斜角α的取值范围是________(其中m≥1).
【答案】2.0°<α≤90°
【解析】当m=1时,直线与x轴垂直,此时斜率不存在,倾斜角为90°.当m>1时,直线的斜率为k===,因为m>1,所以k>0,故直线的倾斜角的取值范围为0°<α<90°.综上可知,直线的倾斜角α的取值范围是0°<α≤90°.
考法03 三点共线
(2021·吉林扶余市第一中学期末)若a∈N,又三点A(a,0),B(0,a+4),C(1,3)共线,求a的值.
【解析】∵A、B、C三点共线,∴直线AC、BC的斜率相等,
∴,解之得,a=±2.
【跟踪训练】
4.已知A(―3,―5),B(1,3),C(5,11)三点,试判断这三点是否在同一直线上.
【解析】由题意可知直线AB的斜率,直线BC的斜率.
因为kAB=kBC,即两条直线的斜率相同,并且它们过同一点B,所以A,B,C三点在同一直线上.
【方法总结】
1.应用斜率公式时应先判定两定点的横坐标是否相等,若相等,直线垂直于x轴,斜率不存在;若不相等,再代入斜率公式求解.
2.用斜率公式可解决三点共线问题
1.知识体系
2.斜率公式
(1)直线的斜率与两点的顺序无关,即两点的纵坐标和横坐标在公式中的次序可以同时调换,就是说, 如果分子是y2-y1,分母必须是x2-x1;反过来,如果分子是y1-y2,分母必须是x1-x2,即k==.
(2)用斜率公式时要一看,二用,三求值.一看,就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第二步;二用,就是将点的坐标代入斜率公式;三求值,就是计算斜率的值,尤其是点的坐标中含有参数时,应用斜率公式时要对参数进行讨论.
【答案】①轴正向 ②倾斜角 ③0° ④0°<180° ⑤ ⑥ ⑦k>0 ⑧90° ⑨增大
题组A 基础过关练
一、单选题
1.直线的倾斜角是( )
A. B. C. D.
【答案】C
【解析】由变形可得,则,又,所以,
2.如图所示,下列四条直线中,斜率最大的是( )
A. B. C. D.
【答案】D
【解析】由图可知:斜率为负,斜率为,的斜率为正,
又的倾斜程度大于,所以的斜率最大,故选:D.
3.如图,在矩形中,,直线的斜率为,则直线的斜率为( )
A. B. C. D.
【答案】A
【解析】由题意,在中,,,
∴,即.
设直线的倾斜角为,则,
∴直线的倾斜角为,故.
故选:A.
4.已知正方形的一条对角线所在直线的斜率为,则其一条边所在直线的斜率是( )
A. B. C. D.
【答案】B
【解析】
以正方形的顶点为坐标原点,建立如图坐标系,
根据题意,对角线的斜率为,设其倾斜角为,
则正方形的倾斜角分别为,
又,
所以两直角边的斜率分别为或.
故选: B.
5.若,,三点共线,则( )
A. B. C. D.
【答案】A
【解析】因为,,故,
因为三点共线,故,故,
故选:A.
6.已知点A(1,0),B(2,),C(m,2m),若直线AC的倾斜角是直线AB的倾斜角的2倍,则实数m的值为________.
【答案】
【解析】设直线AB的倾斜角为α,则直线AC的倾斜角为2α,又tanα=,0°≤α<180°,所以α=60°,2α=120°,
所以kAC==tan120°=,得m=.
故答案为:
7.若A(a,0),B(0,b),C(,)三点共线,则________.
【答案】
【解析】由题意得,
ab+2(a+b)=0,.
故答案为:.
8.若直线经过,两点,则直线的倾斜角的大小是________.
【答案】
【解析】设直线的倾斜角为,
因为直线经过,两点,
所以直线的斜率,
所以,
因为,所以,
故答案为:
题组B 能力提升练
1.直线:与轴交于点,把绕点顺时针旋转得直线,的倾斜角为,则( )
A. B.
C. D.
【答案】C
【解析】设的倾斜角为,则,∴,
由题意知,
∴
.故选:C.
2.直线xsinα-y+2=0的倾斜角的取值范围是( )
A. B.
C. D.
【答案】B
【解析】直线的斜率为,
∵, ∴
∴倾斜角的取值范围是.故选:B.
3.直线的倾斜角的取值范围是( )
A. B. C. D.
【答案】A
【解析】设直线的倾斜角为,
当时,;
当时,则.
因为
所以
综上可得:.
故选:A
4.下列命题中,正确的是( )
A.若直线的倾斜角越大,则直线的斜率就越大
B.若直线的倾斜角为,则直线的斜率为
C.若直线倾斜角,则斜率的取值范围是
D.当直线的倾斜角时,直线的斜率在这个区间上单调递增.
【答案】C
【解析】倾斜角的范围为时,直线斜率,倾斜角的范围为时,直线斜率,故A错误;直线的倾斜角时,直线斜率不存在,故B错误;直线倾斜角,则斜率的范围为,故C正确;斜率在和上单调递增,故D错误.故选:C.
5.已知直线与两点,点,若直线与线段有公共点,则实数的取值范围是______.
【答案】
【解析】由条件得有解,解得,
由,得或.
故答案为:.
6.已知直线的倾斜角为,则的取值范围是_________.
【答案】
【解析】当时,直线为,斜率不存在,倾斜角;
当时,直线化为直线的斜截式方程:
斜率,即,
综上可知,倾斜角的取值范围是
故答案为:
7.已知直线.
(1)若直线过点,试写出直线的一个方向向量;
(2)若实数,求直线的倾斜角的取值范围.
【解析】(1)把代入直线的方程,得,解得,此时直线的方程为,
故直线的一个方向向量为;
(2)因为,所以直线的斜率,
∴当时,当且仅当时等号成立;
当时,当且仅当时等号成立;
综上有,可得倾斜角.
8.已知坐标平面内两点M(m+3,2m+5),N(m-2,1).
(1)当m为何值时,直线MN的倾斜角为锐角?
(2)当m为何值时,直线MN的倾斜角为钝角?
(3)直线MN的倾斜角可能为直角吗?
【解析】(1)若倾斜角为锐角,则斜率大于0,
即k==>0,
解得m>-2.
(2)若倾斜角为钝角,则斜率小于0,
即k==<0,
解得m<-2.
(3)当直线MN垂直于x轴时直线的倾斜角为直角,此时m+3=m-2,此方程无解,故直线MN的倾斜角不可能为直角.
题组C 培优拔尖练
1.2020年12月4日,嫦娥五号探测器在月球表面第一次动态展示国旗.1949年公布的《国旗制法说明》中就五星的位置规定:大五角星有一个角尖正向上方,四颗小五角星均各有一个角尖正对大五角星的中心点.有人发现,第三颗小星的姿态与大星相近.为便于研究,如图,以大星的中心点为原点,建立直角坐标系,,,,分别是大星中心点与四颗小星中心点的联结线,,则第三颗小星的一条边AB所在直线的倾斜角约为( )
A. B. C. D.
【答案】C
【解析】都为五角星的中心点,平分第三颗小星的一个角,
又五角星的内角为,可知,
过作轴平行线,则,所以直线的倾斜角为,
故选:C
2.坐标平面内有相异两点,,经过两点的直线的的倾斜角的取值范围是( )
A. B.
C. D.
【答案】B
【解析】因为点,是相异两点,
,且,
设直线的倾斜角为,则
当,倾斜角的范围为.
当,倾斜角的范围为.
故选:B
3.已知点,若,则直线AB的倾斜角的取值范围为( )
A. B. C. D.
【答案】B
【解析】因为,所以,
因为,所以,
设倾斜角为,,则,
所以.故选:B
4.下列说法错误的是( )
A.“”是“直线与直线互相垂直”的充要条件;
B.直线与直线互相平行,则;
C.过两点的所有直线的方程为;
D.经过点且在x轴和y轴上截距都相等的直线方程为.
【答案】ABCD
【解析】对于:当时,“直线与直线互相垂直”,
当直线与直线互相垂直时,即解得或,
故“”是“直线与直线互相垂直”的充分不必要条件,故错误.
对于:直线与直线互相平行,所以解得或,经检验或都成立;故错误;
对于:过,,,(且,两点的所有直线的方程为,故错误.
对于:经过点且在轴和轴上截距都相等的直线方程为:
故①:经过原点的直线为,②设在坐标轴上的截距为,设直线方程为所以,解得,故,故错误.
故选:.
5.若正方形一条对角线所在直线的斜率为2,则该正方形的两条邻边所在直线的斜率分别为______,_____.
【答案】
【解析】正方形OABC中,对角线OB所在直线的斜率为2,建立如图直角坐标系,
设对角线OB所在直线的倾斜角为,则,
由正方形性质可知,直线的倾斜角为,直线的倾斜角为,
故,
.
故答案为:;.
6.颗粒物过滤效率是衡量口罩防护效果的一个重要指标,计算公式为,其中 表示单位体积环境大气中含有的颗粒物数量(单位:),表示经口罩过滤后,单位体积气体中含有的颗粒物数量(单位:).某研究小组在相同的条件下,对两种不同类型口罩的颗粒物过滤效率分别进行了4次测试,测试结果如图所示.图中点的横坐标表示第i种口罩第j次测试时的值,纵坐标表示第i种口罩第j次测试时的值.
该研究小组得到以下结论:
①在第1种口罩的4次测试中,第4次测试时的颗粒物过滤效率最高;
②在第2种口罩的4次测试中,第3次测试时的颗粒物过滤效率最高;
③在每次测试中,第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率高;
④在第3次和第4次测试中,第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率低.
其中,所有正确结论的序号是__________.
【答案】②④
【解析】依题意,,知直线的斜率越大,颗粒物过滤效率越小. 看图分析如下:
在第1种口罩的4次测试中,四条直线中,直线斜率最大,故最小,第4次测试时的颗粒物过滤效率最低,则①错误;
在第2种口罩的4次测试中,四条直线中,直线斜率最小,故最大,第3次测试时的颗粒物过滤效率最高,则②正确;
在第1次和第2次测试中,直线斜率大于斜率,,即第1种口罩的颗粒物过滤效率高,在第3次和第4次测试中,斜率大于直线,斜率,即第2种口罩的颗粒物过滤效率高,故③错误,④正确.
故答案为:②④.
(1)与相等的向量共有几个;
(2)与方向相同且模为的向量共有几个;
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
课堂小结
直线的倾斜角与斜率
倾斜角
斜率
当直线与轴相交时,我们取轴作为基准, ① 与直线向上方向之间所成的角叫做直线的 ② .当直线和轴平行或重合时,我们规定直线的倾斜角为 ③ ,因此,倾斜角的取值范围是 ④
斜率公式:在直角坐标平面内,已知两点,经过这两点的直线的斜率k= ⑤
倾斜角不是90°的直线的倾斜角的正切值叫做这条直线的斜率.直线的斜率常用表示,即k= ⑥
分层提分
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
课堂小结
直线的倾斜角与斜率
倾斜角
斜率
当直线与轴相交时,我们取轴作为基准, ① 与直线向上方向之间所成的角叫做直线的 ② .当直线和轴平行或重合时,我们规定直线的倾斜角为 ③ ,因此,倾斜角的取值范围是 ④
斜率公式:在直角坐标平面内,已知两点,经过这两点的直线的斜率k= ⑤
倾斜角不是90°的直线的倾斜角的正切值叫做这条直线的斜率.直线的斜率常用表示,即k= ⑥
分层提分
8 / 22
第01讲 直线的斜率与倾斜角
课程标准 重难点
理解直线的斜率和倾斜角的概念;理解直线倾斜角的唯一性及直线斜率的存在性;3.了解斜率公式的推导过程,会应用斜率公式求直线的斜率. 1.倾斜角永远存在但斜率不一定2.倾斜角与斜率的计算
知识点一 直线的倾斜角
在平面直角坐标系中,当直线与轴相交时,我们以轴为基准,轴正向与直线向上的方向之间所成的角叫做直线的倾斜角。
规定:当直线和轴平行或重合时,直线倾斜角为,所以倾斜角的范围是.
【概念解读】
1.要清楚定义中含有的三个条件:①直线向上方向;②轴正向;③小于的角.
2.从运动变化观点来看,直线的倾斜角是由轴按逆时针方向旋转到与直线重合时所成的角.
3.倾斜角的范围是.当时,直线与x轴平行或与x轴重合.
4.直线的倾斜角描述了直线的倾斜程度,每一条直线都有唯一的倾斜角和它对应.
5.已知直线的倾斜角不能确定直线的位置,但是,直线上的一点和这条直线的倾斜角可以唯一确定直线的位置.
知识点二 直线的斜率
斜率的定义
1..倾斜角不是的直线,它的倾斜角的正切叫做这条直线的斜率,常用表示,即.
2.概念解读:当直线与x轴平行或重合时,=0°,k=tan0°=0;直线与x轴垂直时,=90°,k不存在。由此可知,一条直线的倾斜角一定存在,但是斜率k不一定存在.
3.直线的倾斜角与斜率之间的关系
图示
倾斜角(范围) α=0° 0°<α<90° α=90° 90°<α<180°
斜率(范围) k=0 k>0 不存在 k<0
斜率公式
1.斜率公式:已知点、,且与轴不垂直,过两点、的直线的斜率公式.
【概念解读】
对于上面的斜率公式要注意下面五点:
(1) 当x1=x2时,公式右边无意义,直线的斜率不存在,倾斜角=90°,直线与x轴垂直;
(2)k与P1、P2顺序无关,即y1,y2和x1,x2在公式中的前后次序可以同时交换,但分子与分母不能交换;
(3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得;
(4)当y1=y2时,斜率k=0,直线的倾斜角=0°,直线与x轴平行或重合;
(5)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到.
考法01 直线的倾斜角
设直线过原点,其倾斜角为,将直线绕坐标原点沿逆时针方向旋转45°,得到直线,则直线1的倾斜角为
【跟踪训练】
1.已知直线l向上方向与y轴正向所成的角为30°,则直线l的倾斜角为________.
【方法总结】
1.解答此类问题要注意根据倾斜角的概念及倾斜角的取值范围解答.
2.求直线的倾斜角主要根据定义来求,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
考法02 直线的斜率
【例2】如图所示,直线的倾斜角,直线与垂直,求,的斜率.
【跟踪训练】
2.若经过A(m,3),B(1,2)两点的直线的倾斜角为45°,则m=________.
3.经过A(m,3),B(1,2)两点的直线的倾斜角α的取值范围是________(其中m≥1).
考法03 三点共线
(2021·吉林扶余市第一中学期末)若a∈N,又三点A(a,0),B(0,a+4),C(1,3)共线,求a的值.
【跟踪训练】
4.已知A(―3,―5),B(1,3),C(5,11)三点,试判断这三点是否在同一直线上.
【方法总结】
1.应用斜率公式时应先判定两定点的横坐标是否相等,若相等,直线垂直于x轴,斜率不存在;若不相等,再代入斜率公式求解.
2.用斜率公式可解决三点共线问题
1.知识体系
2.斜率公式
(1)直线的斜率与两点的顺序无关,即两点的纵坐标和横坐标在公式中的次序可以同时调换,就是说, 如果分子是y2-y1,分母必须是x2-x1;反过来,如果分子是y1-y2,分母必须是x1-x2,即k==.
(2)用斜率公式时要一看,二用,三求值.一看,就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第二步;二用,就是将点的坐标代入斜率公式;三求值,就是计算斜率的值,尤其是点的坐标中含有参数时,应用斜率公式时要对参数进行讨论.
题组A 基础过关练
一、单选题
1.直线的倾斜角是( )
A. B. C. D.
2.如图所示,下列四条直线中,斜率最大的是( )
A. B. C. D.
3.如图,在矩形中,,直线的斜率为,则直线的斜率为( )
A. B. C. D.
4.已知正方形的一条对角线所在直线的斜率为,则其一条边所在直线的斜率是( )
A. B. C. D.
5.若,,三点共线,则( )
A. B. C. D.
6.已知点A(1,0),B(2,),C(m,2m),若直线AC的倾斜角是直线AB的倾斜角的2倍,则实数m的值为________.
7.若A(a,0),B(0,b),C(,)三点共线,则________.
8.若直线经过,两点,则直线的倾斜角的大小是________.
题组B 能力提升练
1.直线:与轴交于点,把绕点顺时针旋转得直线,的倾斜角为,则( )
A. B.
C. D.
2.直线xsinα-y+2=0的倾斜角的取值范围是( )
A. B.
C. D.
3.直线的倾斜角的取值范围是( )
A. B. C. D.
4.下列命题中,正确的是( )
A.若直线的倾斜角越大,则直线的斜率就越大
B.若直线的倾斜角为,则直线的斜率为
C.若直线倾斜角,则斜率的取值范围是
D.当直线的倾斜角时,直线的斜率在这个区间上单调递增.
5.已知直线与两点,点,若直线与线段有公共点,则实数的取值范围是______.
6.已知直线的倾斜角为,则的取值范围是_________.
7.已知直线.
(1)若直线过点,试写出直线的一个方向向量;
(2)若实数,求直线的倾斜角的取值范围.
8.已知坐标平面内两点M(m+3,2m+5),N(m-2,1).
(1)当m为何值时,直线MN的倾斜角为锐角?
(2)当m为何值时,直线MN的倾斜角为钝角?
(3)直线MN的倾斜角可能为直角吗?
题组C 培优拔尖练
1.2020年12月4日,嫦娥五号探测器在月球表面第一次动态展示国旗.1949年公布的《国旗制法说明》中就五星的位置规定:大五角星有一个角尖正向上方,四颗小五角星均各有一个角尖正对大五角星的中心点.有人发现,第三颗小星的姿态与大星相近.为便于研究,如图,以大星的中心点为原点,建立直角坐标系,,,,分别是大星中心点与四颗小星中心点的联结线,,则第三颗小星的一条边AB所在直线的倾斜角约为( )
A. B. C. D.
2.坐标平面内有相异两点,,经过两点的直线的的倾斜角的取值范围是( )
A. B.
C. D.
3.已知点,若,则直线AB的倾斜角的取值范围为( )
A. B. C. D.
4.下列说法错误的是( )
A.“”是“直线与直线互相垂直”的充要条件;
B.直线与直线互相平行,则;
C.过两点的所有直线的方程为;
D.经过点且在x轴和y轴上截距都相等的直线方程为.
5.若正方形一条对角线所在直线的斜率为2,则该正方形的两条邻边所在直线的斜率分别为______,_____.
6.颗粒物过滤效率是衡量口罩防护效果的一个重要指标,计算公式为,其中 表示单位体积环境大气中含有的颗粒物数量(单位:),表示经口罩过滤后,单位体积气体中含有的颗粒物数量(单位:).某研究小组在相同的条件下,对两种不同类型口罩的颗粒物过滤效率分别进行了4次测试,测试结果如图所示.图中点的横坐标表示第i种口罩第j次测试时的值,纵坐标表示第i种口罩第j次测试时的值.
该研究小组得到以下结论:
①在第1种口罩的4次测试中,第4次测试时的颗粒物过滤效率最高;
②在第2种口罩的4次测试中,第3次测试时的颗粒物过滤效率最高;
③在每次测试中,第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率高;
④在第3次和第4次测试中,第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率低.
其中,所有正确结论的序号是__________.
(1)与相等的向量共有几个;
(2)与方向相同且模为的向量共有几个;
第1章 直线与方程答案
第01讲 直线的斜率与倾斜角
课程标准 重难点
理解直线的斜率和倾斜角的概念;理解直线倾斜角的唯一性及直线斜率的存在性;3.了解斜率公式的推导过程,会应用斜率公式求直线的斜率. 1.倾斜角永远存在但斜率不一定2.倾斜角与斜率的计算
知识点一 直线的倾斜角
在平面直角坐标系中,当直线与轴相交时,我们以轴为基准,轴正向与直线向上的方向之间所成的角叫做直线的倾斜角。
规定:当直线和轴平行或重合时,直线倾斜角为,所以倾斜角的范围是.
【概念解读】
1.要清楚定义中含有的三个条件:①直线向上方向;②轴正向;③小于的角.
2.从运动变化观点来看,直线的倾斜角是由轴按逆时针方向旋转到与直线重合时所成的角.
3.倾斜角的范围是.当时,直线与x轴平行或与x轴重合.
4.直线的倾斜角描述了直线的倾斜程度,每一条直线都有唯一的倾斜角和它对应.
5.已知直线的倾斜角不能确定直线的位置,但是,直线上的一点和这条直线的倾斜角可以唯一确定直线的位置.
知识点二 直线的斜率
斜率的定义
1..倾斜角不是的直线,它的倾斜角的正切叫做这条直线的斜率,常用表示,即.
2.概念解读:当直线与x轴平行或重合时,=0°,k=tan0°=0;直线与x轴垂直时,=90°,k不存在。由此可知,一条直线的倾斜角一定存在,但是斜率k不一定存在.
3.直线的倾斜角与斜率之间的关系
图示
倾斜角(范围) α=0° 0°<α<90° α=90° 90°<α<180°
斜率(范围) k=0 k>0 不存在 k<0
斜率公式
1.斜率公式:已知点、,且与轴不垂直,过两点、的直线的斜率公式.
【概念解读】
对于上面的斜率公式要注意下面五点:
(1) 当x1=x2时,公式右边无意义,直线的斜率不存在,倾斜角=90°,直线与x轴垂直;
(2)k与P1、P2顺序无关,即y1,y2和x1,x2在公式中的前后次序可以同时交换,但分子与分母不能交换;
(3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得;
(4)当y1=y2时,斜率k=0,直线的倾斜角=0°,直线与x轴平行或重合;
(5)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到.
考法01 直线的倾斜角
设直线过原点,其倾斜角为,将直线绕坐标原点沿逆时针方向旋转45°,得到直线,则直线1的倾斜角为
【答案】当0°≤<135°时,为+45°,当135°≤<180°时,为-135°
【解析】倾斜角的范围是[0°,180°),因此,只有当+45°∈[0°,180°),即当0°≤<135°时,的倾斜角才是+45°,而当135°≤<180°时,的倾斜角为-135°.故应选D.
【跟踪训练】
1.已知直线l向上方向与y轴正向所成的角为30°,则直线l的倾斜角为________.
【答案】60°或120°
【解析】有两种情况:①如图(1),直线l向上方向与x轴正向所成的角为60°,即直线l的倾斜角为60°.
②如图(2),直线l向上方向与x轴正向所成的角为120°,即直线l的倾斜角为120°.
【方法总结】
1.解答此类问题要注意根据倾斜角的概念及倾斜角的取值范围解答.
2.求直线的倾斜角主要根据定义来求,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论.
考法02 直线的斜率
【例2】如图所示,直线的倾斜角,直线与垂直,求,的斜率.
【解析】由图形可知,,则k1,k2可求.
直线的斜率.
∵直线的倾斜角=90°+30°=120°,
∴直线的斜率k2=tan120°=tan(180°―60°)=―tan60°=.
【跟踪训练】
2.若经过A(m,3),B(1,2)两点的直线的倾斜角为45°,则m=________.
【答案】1.2
【解析】tan 45°=,得m=2.
3.经过A(m,3),B(1,2)两点的直线的倾斜角α的取值范围是________(其中m≥1).
【答案】2.0°<α≤90°
【解析】当m=1时,直线与x轴垂直,此时斜率不存在,倾斜角为90°.当m>1时,直线的斜率为k===,因为m>1,所以k>0,故直线的倾斜角的取值范围为0°<α<90°.综上可知,直线的倾斜角α的取值范围是0°<α≤90°.
考法03 三点共线
(2021·吉林扶余市第一中学期末)若a∈N,又三点A(a,0),B(0,a+4),C(1,3)共线,求a的值.
【解析】∵A、B、C三点共线,∴直线AC、BC的斜率相等,
∴,解之得,a=±2.
【跟踪训练】
4.已知A(―3,―5),B(1,3),C(5,11)三点,试判断这三点是否在同一直线上.
【解析】由题意可知直线AB的斜率,直线BC的斜率.
因为kAB=kBC,即两条直线的斜率相同,并且它们过同一点B,所以A,B,C三点在同一直线上.
【方法总结】
1.应用斜率公式时应先判定两定点的横坐标是否相等,若相等,直线垂直于x轴,斜率不存在;若不相等,再代入斜率公式求解.
2.用斜率公式可解决三点共线问题
1.知识体系
2.斜率公式
(1)直线的斜率与两点的顺序无关,即两点的纵坐标和横坐标在公式中的次序可以同时调换,就是说, 如果分子是y2-y1,分母必须是x2-x1;反过来,如果分子是y1-y2,分母必须是x1-x2,即k==.
(2)用斜率公式时要一看,二用,三求值.一看,就是看所给两点的横坐标是否相等,若相等,则直线的斜率不存在,若不相等,则进行第二步;二用,就是将点的坐标代入斜率公式;三求值,就是计算斜率的值,尤其是点的坐标中含有参数时,应用斜率公式时要对参数进行讨论.
【答案】①轴正向 ②倾斜角 ③0° ④0°<180° ⑤ ⑥ ⑦k>0 ⑧90° ⑨增大
题组A 基础过关练
一、单选题
1.直线的倾斜角是( )
A. B. C. D.
【答案】C
【解析】由变形可得,则,又,所以,
2.如图所示,下列四条直线中,斜率最大的是( )
A. B. C. D.
【答案】D
【解析】由图可知:斜率为负,斜率为,的斜率为正,
又的倾斜程度大于,所以的斜率最大,故选:D.
3.如图,在矩形中,,直线的斜率为,则直线的斜率为( )
A. B. C. D.
【答案】A
【解析】由题意,在中,,,
∴,即.
设直线的倾斜角为,则,
∴直线的倾斜角为,故.
故选:A.
4.已知正方形的一条对角线所在直线的斜率为,则其一条边所在直线的斜率是( )
A. B. C. D.
【答案】B
【解析】
以正方形的顶点为坐标原点,建立如图坐标系,
根据题意,对角线的斜率为,设其倾斜角为,
则正方形的倾斜角分别为,
又,
所以两直角边的斜率分别为或.
故选: B.
5.若,,三点共线,则( )
A. B. C. D.
【答案】A
【解析】因为,,故,
因为三点共线,故,故,
故选:A.
6.已知点A(1,0),B(2,),C(m,2m),若直线AC的倾斜角是直线AB的倾斜角的2倍,则实数m的值为________.
【答案】
【解析】设直线AB的倾斜角为α,则直线AC的倾斜角为2α,又tanα=,0°≤α<180°,所以α=60°,2α=120°,
所以kAC==tan120°=,得m=.
故答案为:
7.若A(a,0),B(0,b),C(,)三点共线,则________.
【答案】
【解析】由题意得,
ab+2(a+b)=0,.
故答案为:.
8.若直线经过,两点,则直线的倾斜角的大小是________.
【答案】
【解析】设直线的倾斜角为,
因为直线经过,两点,
所以直线的斜率,
所以,
因为,所以,
故答案为:
题组B 能力提升练
1.直线:与轴交于点,把绕点顺时针旋转得直线,的倾斜角为,则( )
A. B.
C. D.
【答案】C
【解析】设的倾斜角为,则,∴,
由题意知,
∴
.故选:C.
2.直线xsinα-y+2=0的倾斜角的取值范围是( )
A. B.
C. D.
【答案】B
【解析】直线的斜率为,
∵, ∴
∴倾斜角的取值范围是.故选:B.
3.直线的倾斜角的取值范围是( )
A. B. C. D.
【答案】A
【解析】设直线的倾斜角为,
当时,;
当时,则.
因为
所以
综上可得:.
故选:A
4.下列命题中,正确的是( )
A.若直线的倾斜角越大,则直线的斜率就越大
B.若直线的倾斜角为,则直线的斜率为
C.若直线倾斜角,则斜率的取值范围是
D.当直线的倾斜角时,直线的斜率在这个区间上单调递增.
【答案】C
【解析】倾斜角的范围为时,直线斜率,倾斜角的范围为时,直线斜率,故A错误;直线的倾斜角时,直线斜率不存在,故B错误;直线倾斜角,则斜率的范围为,故C正确;斜率在和上单调递增,故D错误.故选:C.
5.已知直线与两点,点,若直线与线段有公共点,则实数的取值范围是______.
【答案】
【解析】由条件得有解,解得,
由,得或.
故答案为:.
6.已知直线的倾斜角为,则的取值范围是_________.
【答案】
【解析】当时,直线为,斜率不存在,倾斜角;
当时,直线化为直线的斜截式方程:
斜率,即,
综上可知,倾斜角的取值范围是
故答案为:
7.已知直线.
(1)若直线过点,试写出直线的一个方向向量;
(2)若实数,求直线的倾斜角的取值范围.
【解析】(1)把代入直线的方程,得,解得,此时直线的方程为,
故直线的一个方向向量为;
(2)因为,所以直线的斜率,
∴当时,当且仅当时等号成立;
当时,当且仅当时等号成立;
综上有,可得倾斜角.
8.已知坐标平面内两点M(m+3,2m+5),N(m-2,1).
(1)当m为何值时,直线MN的倾斜角为锐角?
(2)当m为何值时,直线MN的倾斜角为钝角?
(3)直线MN的倾斜角可能为直角吗?
【解析】(1)若倾斜角为锐角,则斜率大于0,
即k==>0,
解得m>-2.
(2)若倾斜角为钝角,则斜率小于0,
即k==<0,
解得m<-2.
(3)当直线MN垂直于x轴时直线的倾斜角为直角,此时m+3=m-2,此方程无解,故直线MN的倾斜角不可能为直角.
题组C 培优拔尖练
1.2020年12月4日,嫦娥五号探测器在月球表面第一次动态展示国旗.1949年公布的《国旗制法说明》中就五星的位置规定:大五角星有一个角尖正向上方,四颗小五角星均各有一个角尖正对大五角星的中心点.有人发现,第三颗小星的姿态与大星相近.为便于研究,如图,以大星的中心点为原点,建立直角坐标系,,,,分别是大星中心点与四颗小星中心点的联结线,,则第三颗小星的一条边AB所在直线的倾斜角约为( )
A. B. C. D.
【答案】C
【解析】都为五角星的中心点,平分第三颗小星的一个角,
又五角星的内角为,可知,
过作轴平行线,则,所以直线的倾斜角为,
故选:C
2.坐标平面内有相异两点,,经过两点的直线的的倾斜角的取值范围是( )
A. B.
C. D.
【答案】B
【解析】因为点,是相异两点,
,且,
设直线的倾斜角为,则
当,倾斜角的范围为.
当,倾斜角的范围为.
故选:B
3.已知点,若,则直线AB的倾斜角的取值范围为( )
A. B. C. D.
【答案】B
【解析】因为,所以,
因为,所以,
设倾斜角为,,则,
所以.故选:B
4.下列说法错误的是( )
A.“”是“直线与直线互相垂直”的充要条件;
B.直线与直线互相平行,则;
C.过两点的所有直线的方程为;
D.经过点且在x轴和y轴上截距都相等的直线方程为.
【答案】ABCD
【解析】对于:当时,“直线与直线互相垂直”,
当直线与直线互相垂直时,即解得或,
故“”是“直线与直线互相垂直”的充分不必要条件,故错误.
对于:直线与直线互相平行,所以解得或,经检验或都成立;故错误;
对于:过,,,(且,两点的所有直线的方程为,故错误.
对于:经过点且在轴和轴上截距都相等的直线方程为:
故①:经过原点的直线为,②设在坐标轴上的截距为,设直线方程为所以,解得,故,故错误.
故选:.
5.若正方形一条对角线所在直线的斜率为2,则该正方形的两条邻边所在直线的斜率分别为______,_____.
【答案】
【解析】正方形OABC中,对角线OB所在直线的斜率为2,建立如图直角坐标系,
设对角线OB所在直线的倾斜角为,则,
由正方形性质可知,直线的倾斜角为,直线的倾斜角为,
故,
.
故答案为:;.
6.颗粒物过滤效率是衡量口罩防护效果的一个重要指标,计算公式为,其中 表示单位体积环境大气中含有的颗粒物数量(单位:),表示经口罩过滤后,单位体积气体中含有的颗粒物数量(单位:).某研究小组在相同的条件下,对两种不同类型口罩的颗粒物过滤效率分别进行了4次测试,测试结果如图所示.图中点的横坐标表示第i种口罩第j次测试时的值,纵坐标表示第i种口罩第j次测试时的值.
该研究小组得到以下结论:
①在第1种口罩的4次测试中,第4次测试时的颗粒物过滤效率最高;
②在第2种口罩的4次测试中,第3次测试时的颗粒物过滤效率最高;
③在每次测试中,第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率高;
④在第3次和第4次测试中,第1种口罩的颗粒物过滤效率都比第2种口罩的颗粒物过滤效率低.
其中,所有正确结论的序号是__________.
【答案】②④
【解析】依题意,,知直线的斜率越大,颗粒物过滤效率越小. 看图分析如下:
在第1种口罩的4次测试中,四条直线中,直线斜率最大,故最小,第4次测试时的颗粒物过滤效率最低,则①错误;
在第2种口罩的4次测试中,四条直线中,直线斜率最小,故最大,第3次测试时的颗粒物过滤效率最高,则②正确;
在第1次和第2次测试中,直线斜率大于斜率,,即第1种口罩的颗粒物过滤效率高,在第3次和第4次测试中,斜率大于直线,斜率,即第2种口罩的颗粒物过滤效率高,故③错误,④正确.
故答案为:②④.
(1)与相等的向量共有几个;
(2)与方向相同且模为的向量共有几个;
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
课堂小结
直线的倾斜角与斜率
倾斜角
斜率
当直线与轴相交时,我们取轴作为基准, ① 与直线向上方向之间所成的角叫做直线的 ② .当直线和轴平行或重合时,我们规定直线的倾斜角为 ③ ,因此,倾斜角的取值范围是 ④
斜率公式:在直角坐标平面内,已知两点,经过这两点的直线的斜率k= ⑤
倾斜角不是90°的直线的倾斜角的正切值叫做这条直线的斜率.直线的斜率常用表示,即k= ⑥
分层提分
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
课堂小结
直线的倾斜角与斜率
倾斜角
斜率
当直线与轴相交时,我们取轴作为基准, ① 与直线向上方向之间所成的角叫做直线的 ② .当直线和轴平行或重合时,我们规定直线的倾斜角为 ③ ,因此,倾斜角的取值范围是 ④
斜率公式:在直角坐标平面内,已知两点,经过这两点的直线的斜率k= ⑤
倾斜角不是90°的直线的倾斜角的正切值叫做这条直线的斜率.直线的斜率常用表示,即k= ⑥
分层提分
8 / 22
