椭圆的标准方程1[上学期]

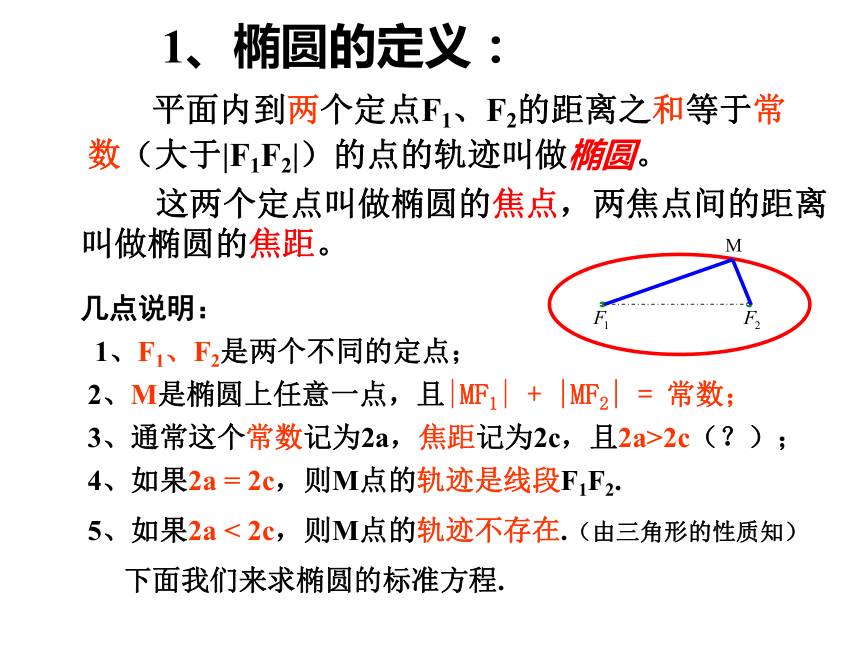
课件18张PPT。椭圆及其标准方程F1F21、椭圆的定义： 平面内到两个定点F1、F2的距离之和等于常数（大于|F1F2|）的点的轨迹叫做椭圆。 这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。几点说明：2、M是椭圆上任意一点，且|MF1| + |MF2| = 常数；3、通常这个常数记为2a，焦距记为2c，且2a>2c（？）；4、如果2a = 2c，则M点的轨迹是线段F1F2.5、如果2a < 2c，则M点的轨迹不存在.（由三角形的性质知） 下面我们来求椭圆的标准方程.1、F1、F2是两个不同的定点；应用举例1.用定义判断下列动点M的轨迹是否为椭圆。(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹。(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹。(3)到F1(-2,0)、F2(2,0)的距离之和为3的点的轨迹。解 (1)因|MF1|+|MF2|=6>|F1F2|=4，故点M的轨迹为椭圆。(2)因|MF1|+|MF2|=4=|F1F2|=4，故点M的轨迹不是椭圆(是线段F1F2)。(3)因|MF1|+|MF2|=4>|F1F2|=3，故点M的轨迹不成图形。二、推导椭圆的标准方程(1)如何求到两个定点 的距离之和等于定值2a 的点的轨迹。(2)求曲线方程的步骤是什么？ 建系设点，列式，代入，化简，证明 (3)那么此题如何建立坐标系呢？ 建立直角坐标系一般应符合简单和谐的原则，注意要充分利用图形的特殊性。OXYF1F2M如图所示： F1、F2为两定点，且|F1F2|=2c，求平面内到两定点F1、F2距离之和为定值2a（2a>2c)的动点M的轨迹方程。 解：以F1F2所在直线为X轴， F1F2 的中点为原点建立平面直角坐标系，则焦点F1、F2的坐标分别为(-c,0)、 (c,0)。(-c,0)(c,0)(x,y) 设M（x,y)为所求轨迹上的任意一点，则:|MF1|+ |MF2|=2aOXYF1F2M(-c,0)(c,0)(x,y)两边平方得：a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2即：(a2-c2)x2+a2y2=a2(a2-c2)因为2a>2c，即a>c，所以a2-c2>0，令a2-c2=b2，其中b>0，代入上式可得：b2x2+a2y2=a2b2两边同时除以a2b2得：(a>b>0)这个方程叫做椭圆的标准方程，
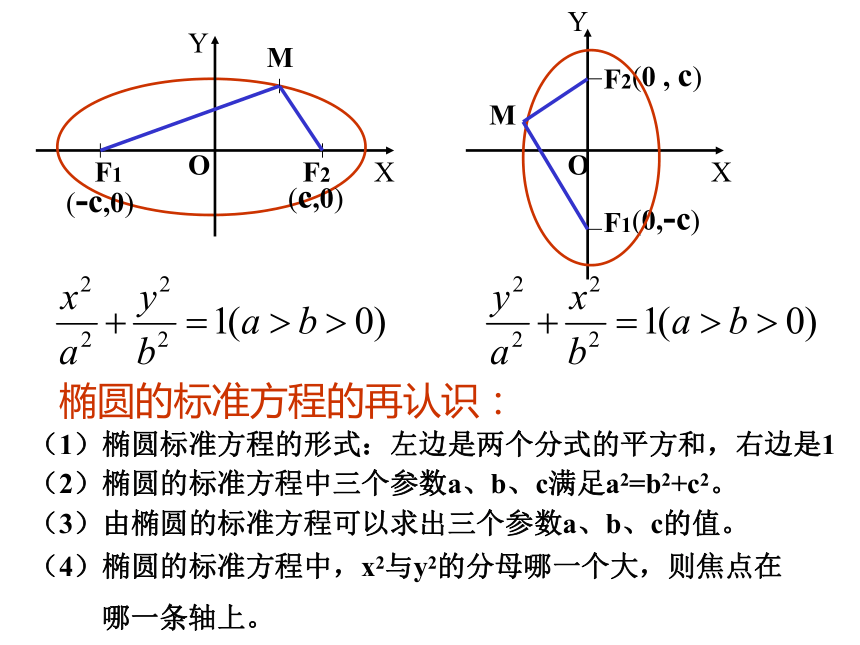
它所表示的椭圆的焦点在x 轴上。OXYF1F2M(-c,0)(c,0)OXYF1F2M(0,-c)(0 , c)椭圆的标准方程的再认识：（1）椭圆标准方程的形式：左边是两个分式的平方和，右边是1（2）椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。（3）由椭圆的标准方程可以求出三个参数a、b、c的值。（4）椭圆的标准方程中，x2与y2的分母哪一个大，则焦点在
哪一条轴上。椭圆的标准方程 定 义图 形方 程焦 点F(±c，0)F(0，±c)a,b,c之间的关系c2=a2-b2|MF1|+|MF2|=2a小 结：判定下列椭圆的焦点在 哪个轴上，并指明a2、b2，写出焦点坐标。答：在 X 轴。（-3，0）和（3，0）答：在 y 轴。（0，-5）和（0，5）答：在y 轴。（0，-1）和（0，1）判断椭圆标准方程的焦点在哪个轴上的准则：
焦点在分母大的那个轴上。应用举例应用举例a>30(1)已知椭圆的方程为： ，则a=_____，b=_______，c=_______，焦点坐标为：____________焦距等于______;若CD为过左焦点F1的弦，则 F2CD的周长为________543(3,0)、(-3,0)620F1F2CD例题讲解(2)已知椭圆的方程为： ，则a=_____，b=_______，c=_______，焦点坐标为：___________焦距等于__________;曲线上一点P到左焦点F1的距离为3，则点P到另一个焦点F2的距离等于_________，则 F1PF2的周长为___________21(0,-1)、(0,1)2例2、求满足下列条件的椭圆的标准方程：（1）满足a=4,b=1，焦点在X轴上的椭圆的标准方程为____________ （2）满足a=4,c= ，焦点在Y轴上的椭圆的标准方程为____________例3 求适合下列条件的椭圆的标准方程：（1）两个焦点的坐标分别是（－4，0）、（4，0），
椭圆上的一点P到两焦点距离的和等于10；变式：两个焦点的距离等于8，椭圆上的一点P到两焦
点距离的和等于10.例4：若方程4x2+ky2=1表示的曲线是焦点在y轴上的椭圆，求k的取值范围。解：由 4x2+ky2=1,可得 因为方程表示的曲线是焦点在y轴上的椭圆，所以即：0 A.椭圆
B.线段F1F2
C.直线F1F2
D.不能确定
B三、小 结： 1、椭圆的定义
2、两种标准方程的比较3、在求椭圆方程时，要弄清焦点
在哪个轴上，是x轴还是y轴？
或者两个轴都有可能？四、布置作业：P96 习题8.1：1、2、3
同步作业本P57