山东省泰安市东平县旧县乡中学2022-2023学年八年级数学上册期末模拟测试题(含解析)
文档属性
| 名称 | 山东省泰安市东平县旧县乡中学2022-2023学年八年级数学上册期末模拟测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 395.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 08:39:08 | ||
图片预览




文档简介
山东省泰安市东平县旧县乡中学2022-2023学年八年级数学上册期末模拟测试题(附答案)
一、选择题(共56分)
1.观察下列图案,既是轴对称图形又是中心对称图形的共有( )
A.4个 B.3个 C.2个 D.1个
2.下列因式分解中:①x3+2xy+x=x(x+2y);②x2+4x+4=(x+2)2;③﹣x2+y2=(x+y)(y﹣x);④x3﹣9x=x(x﹣3)2,正确的个数为( )
A.1个 B.2个 C.3个 D.4个
3.若正多边形的内角和是1080°,则该正多边形的一个外角为( )
A.45° B.60° C.72° D.90°
4.在四边形ABCD中,O是对角线交点,下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AD∥BC,AD=BC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OD=OB
5.如图,在平行四边形ABCD中,AB=4,BC=6,对角线AC、BD相交于点O,则OA的取值范围是( )
A.2<OA<10 B.1<OA<5 C.4<OA<6 D.2<OA<8
6.下列各分式中,是最简分式的是( )
A. B. C. D.
7.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )
A.70° B.65° C.60° D.55°
8.某校为了丰富学生的校园生活,准备购进一批篮球和足球,其中篮球的单价比足球的单价多20元.李老师购买篮球花费900元,购买足球花费400元,结果购得的篮球数量是足球数量的1.5倍.设购买的足球数量是x个,则下列选项中所列方程正确的是( )
A.=+20 B.=+20
C.=+20 D.=+20
9.关于x的分式方程有增根,则m的值为( )
A.2 B.3 C.4 D.5
10.对于一组统计数据3,3,6,5,3.下列说法错误的是( )
A.众数是3 B.平均数是4 C.方差是1.6 D.中位数是6
11.在 ABCD中,EF过对角线的交点O,AB=4,BC=5,OF=1.5,则四边形ABFE的周长是( )
A.11 B.11.5 C.12 D.12.5
12.若关于x的分式方程=1的解为正数,且关于y的不等式组至少两个整数解,则符合条件的所有整数m的取值之和为( )
A.﹣7 B.﹣9 C.﹣12 D.﹣14
13.如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )
A.14 B.16 C.18 D.20
14.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )
A. B.2 C. D.3
二、填空题(共32分.)
15.因式分解:m3﹣6m2+9m= .
16.在平行四边形ABCD中,AD=BD,BE是AD边上的高,∠EBD=10°,则∠A的度数为 .
17.如图,直线AE∥BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
18.如图,△ABC的边长AB=3cm,BC=4cm,AC=2cm,将△ABC沿BC方向平移acm(a<4),得到△DEF,连接AD,则阴影部分的周长为 cm.
19.已知a+b=5,ab=3,则代数式a3b+2a2b2+ab3= .
20.若分式的值为0,则x= .
21.在平面直角坐标系中,点A(﹣5,b)关于原点对称的点为B(a,6),则(a+b)2022= .
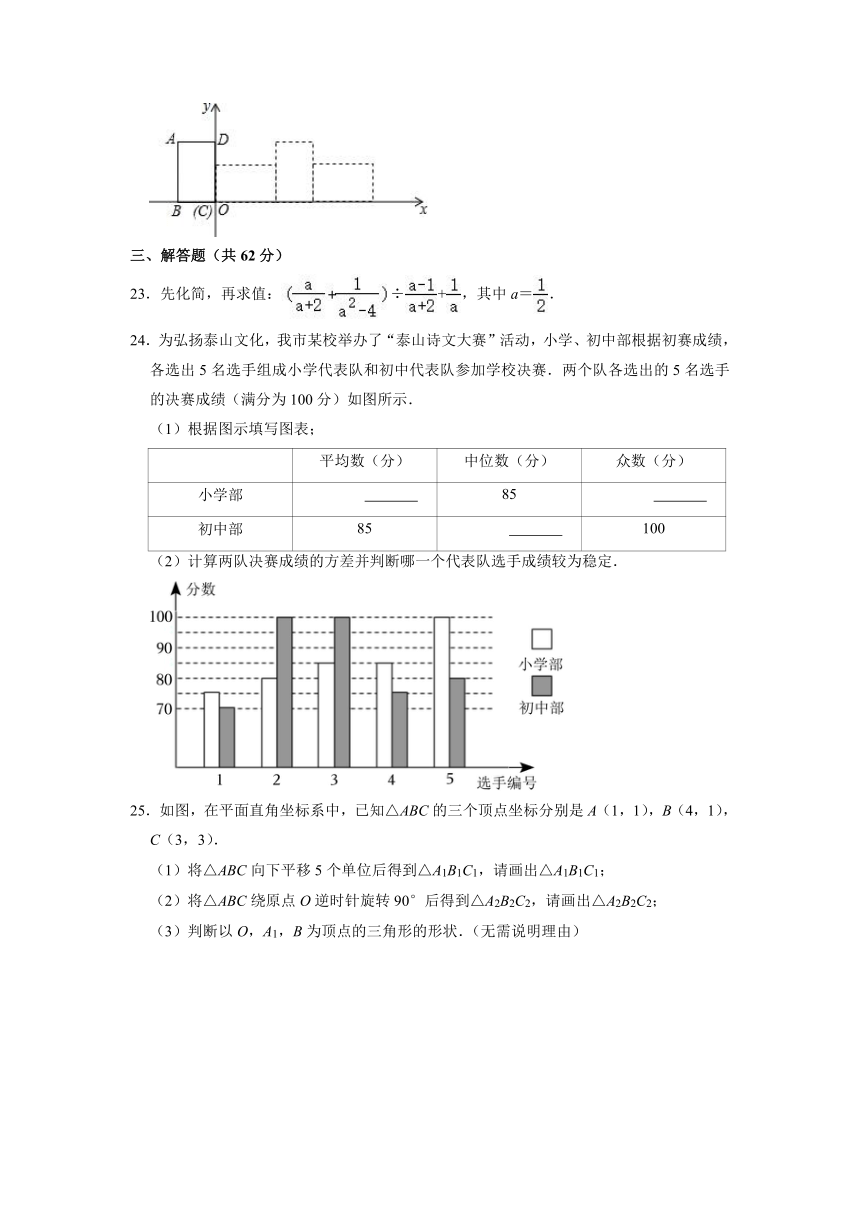
22.如图,长方形ABCD的两边BC,CD分别在x轴、y轴上,点C与原点重合,点A(﹣1,2),将长方形ABCD沿x轴无滑动向右翻滚,经过一次翻滚,点A对应点记为A1;经过第二次翻滚,点A对应点记为A2;…;依此类推,经过第2020次翻滚,点A对应点A2020坐标为 .
三、解答题(共62分)
23.先化简,再求值:÷+,其中a=.
24.为弘扬泰山文化,我市某校举办了“泰山诗文大赛”活动,小学、初中部根据初赛成绩,各选出5名选手组成小学代表队和初中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩(满分为100分)如图所示.
(1)根据图示填写图表;
平均数(分) 中位数(分) 众数(分)
小学部 85
初中部 85 100
(2)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
25.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无需说明理由)
26.如图①,平行四边形ABCD的对角线AC,BD相交于点O,EF过点O与AB,CD分别相交于点E,F.
(1)求证:BE=DF;
(2)若图中的条件都不变,将EF转动到图②的位置,那么上述结论是否成立?说明理由.
27.某个体经营户了解到有一种盒装商品能畅销市场,就用4万元购进这种商品,面市后果然供不应求,他又用8.8万元购进了第二批这种商品,所购数量是第一批购进量的2倍,但每盒单价涨了4元,他在销售这种盒装商品时每盒定价都是56元,最后剩下的150盒按八折销售,很快售完,在这两笔生意中,这位个体经营户共赢利多少元?
28.(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是 ;位置关系是 .
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.
参考答案
选择题(共56分)
1.解:第1个是轴对称图形,不是中心对称图形,故此选项不合题意;
第2个是轴对称图形,也是中心对称图形,故此选项符合题意;
第3个是轴对称图形,也是中心对称图形,故此选项符合题意;
第4个不是轴对称图形,是中心对称图形,故此选项不合题意.
故选:C.
2.解:①x3+2xy+x=x(x2+2y+1),故原题分解错误;
②x2+4x+4=(x+2)2,故原题分解正确;
③﹣x2+y2=y2﹣x2=(x+y)(y﹣x),故原题分解正确;
④x3﹣9x=x(x2﹣9)=x(x+3)(x﹣3),故原题分解错误;
正确的个数为2个,
故选:B.
3.解:设这个正多边形的边数为n,
∵一个正多边形的内角和为1080°,
∴180(n﹣2)=1080,
解得:n=8,
∴这个正多边形的每一个外角是:360°÷8=45°.
故选:A.
4.解:A、根据一组对边平行且相等的四边形是平行四边形,可以判定,故正确;
B、根据平行四边形的定义即可判定,故正确;
C、一组对边平行,另一组对边相等的四边形,等腰梯形满足条件.故该选项错误.
D、根据对角线互相平分的四边形是平行四边形可以判定.故正确.
故选:C.
5.解:∵AB=4,BC=6,
∴2<AC<10,
∵四边形ABCD是平行四边形,
∴AO=AC,
∴1<OA<5,
故选:B.
6.解:A.是最简分式;
B.==x﹣y,不符合题意;
C.==,不符合题意;
D.=,不符合题意;
故选:A.
7.解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,
∴AC=A′C,
∴△ACA′是等腰直角三角形,
∴∠CAA′=45°,
∴∠A′B′C=∠1+∠CAA′=20°+45°=65°,
由旋转的性质得∠B=∠A′B′C=65°.
故选:B.
8.解:设购买的足球数量是x个,则购买篮球数量是1.5x个,
根据题意,得=+20.
故选:C.
9.解:去分母得5x+3(x﹣1)=2m+1,
解得x=,
因为原方程的增根为x=1,
所以=1,解得m=2,
即m=2时,分式方程有增根.
故选:A.
10.解:将这组数据重新排列为3、3、3、5、6,
∴这组数据的众数为3,
平均数为=4,
方差为×[3×(3﹣4)2+(5﹣4)2+(6﹣4)2]=1.6,
中位数为3,
故选:D.
11.解:已知AB=4,BC=5,OE=1.5,
根据平行四边形的性质,AB=CD=4,BC=AD=5,
在△AEO和△CFO中OA=OC,∠OAE=∠OCF,∠AOE=∠COF,
所以△AEO≌△CFO,OE=OF=1.5,
则ABFE的周长=EFCD的周长=ED+CD+CF+EF=(DE+CF)+AB+EF=5+4+3=12.
故选:C.
12.解:由方程=1,解得:x=﹣2﹣m,
则
可得:m<﹣2且m≠﹣5,
由①知,y>﹣2,
由②知,y≤,
∵关于y的不等式组至少两个整数解,
∴y=﹣1和0
∴5+m≥0,
解得:m≥﹣5,
所以m的整数值为﹣4,﹣3,
﹣4+(﹣3)=﹣7,
故选:A.
13.解:∵线段AB平移得到线段CD,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵A(1,0),B(4,0),
∴AB=4﹣1=3,
∵四边形ABCD的面积为9,
∴3 OC=9,
解得OC=3,
在Rt△BOC中,由勾股定理得,BC===5,
∴四边形ABCD的周长=2(3+5)=16.
故选:B.
14.解:∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,
∴△BNA≌△BNE,
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点N是AE中点,点M是AD中点(三线合一),
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=19﹣BC=19﹣7=12,
∴DE=BE+CD﹣BC=5,
∴MN=DE=.
故选:C.
二、填空题(共32分.)
15.解:m3﹣6m2+9m=m(m2﹣6m+9)=m(m﹣3)2,
故答案为:m(m﹣3)2.
16.解:情形一:当E点在线段AD上时,如图所示,
∵BE是AD边上的高,∠EBD=10°,
∴∠ADB=90°﹣10°=80°,
∵AD=BD,
∴∠A=∠ABD=(180°﹣80°)÷2=50°;
情形二:当E点在AD的延长线上时,如图所示,
∵BE是AD边上的高,∠EBD=10°,
∴∠BDE=80°,
∵AD=BD,
∴∠A=∠ABD=∠BDE=40°.
故答案为:50°或40°.
17.解:过点A作AF⊥BD于点F,
∵△ABD的面积为16,BD=8,
∴BD AF=×8×AF=16,
解得AF=4,
∵AE∥BD,
∴AF的长是△ACE的高,
∴S△ACE=×AE×4=×5×4=10.
故答案为:10.
18.解:∵将△ABC沿BC方向平移acm(a<4cm),得到△DEF,
∴AD=BE,AB=DE,AC=DF,
∴阴影部分的周长=AD+EC+DE+AC=BE+EC+AC+AB=AB+AC+BC=3+4+2=9cm,
故答案为:9.
19.解:原式=ab(a2+2ab+b2)=ab(a+b)2,
当a+b=5,ab=3时,原式=3×52=75.
故答案是:75.
20.解:∵x2﹣4=0,
∴x=±2,
当x=2时,x+2≠0,
当x=﹣2时,x+2=0.
∴当x=2时,分式的值是0.
故答案为:2.
21.解:∵点A(﹣5,b)关于原点对称的点为B(a,6),
∴a=5,b=﹣6,
则(a+b)2022=(5﹣6)2022=1.
故答案为:1.
22.解:如图所示:
观察图形可得经过4次翻滚后点A对应点一循环,
2020÷4=505,
∵点A(﹣1,2),长方形的周长为:2(1+2)=6,
∴经过505次翻滚后点A对应点A2020的坐标为(6×505﹣1,2),即(3029,2).
故答案为:(3029,2).
三、解答题(共62分)
23.解:原式=[+]×+
=×==,
把a=代入得,
原式==.
24.解:(1)填表:小学部平均数:(75+80+85+85+100)÷5=85(分);
小学部得分中85出现的次数最多,则小学部的众数为85分;
初中部得分情况为70,75,80,100,100,则初中部的中位数为80分.
(2)∵=[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,,
∴,
因此,小学代表队选手成绩较为稳定.
25.解:(1)如图所示,△A1B1C1即为所求:
(2)如图所示,△A2B2C2即为所求:
(3)三角形的形状为等腰直角三角形,OB=OA1=,A1B=,
即,
所以三角形的形状为等腰直角三角形.
26.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OB=OD,
∴∠OBE=∠ODF,
在△OBE和△ODF中,
,
∴△OBE≌△ODF(ASA),
∴BE=DF;
(2)解:结论成立,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,OB=OD,
∴∠OAE=∠OCF,∠OEF=∠OFC
在△OAE和△OCF中,
,
∴△OAE≌△OCF(AAS),
∴OE=OF,
在△OBE和△ODF中,
,
∴△OBE≌△ODF(SAS),
∴BE=DF.
27.解:设第一批进货的单价为x元,则第二批进货的单价为(x+4)元,依题意有
×2=,
解得:x=40,
经检验x=40是原分式方程的解,且符合题意,
则第一次进货1000件,
第二次进货的单价为44元,第二次进货2000件,
总盈利为:(56﹣40)×1000+(56﹣44)×(2000﹣150)+150×(56×0.8﹣44)
=16000+22200+120
=38320(元).
答:这位个体经营户共赢利38320元.
28.解:(1)如图①,连接BE,CD相交于H,
∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=90°
∴∠CAD=∠BAE,
∴△ACD≌△AEB(SAS),
∴CD=BE,∠ADC=∠ABE,
∴∠BDC+∠DBH=∠BDC+∠ABD+∠ABE=∠BDC+∠ABD+∠ADC=∠ADB+∠ABD=90°,
∴∠BHD=90°,
∴CD⊥BE,
∵点M,G分别是BD,BC的中点,
∴MGCD,
同理:NGBE,
∴MG=NG,MG⊥NG,
故答案为:MG=NG,MG⊥NG;
(2)如图②,连接CD,BE相交于点H,
同(1)的方法得,MG=NG,MG⊥NG;
(3)如图③,连接EB,DC,延长线相交于H,
同(1)的方法得,MG=NG,
同(1)的方法得,△ABE≌△ADC,
∴∠AEB=∠ACD,
∴∠CEH+∠ECH=∠AEH﹣∠AEC+180°﹣∠ACD﹣∠ACE=∠ACD﹣45°+180°﹣∠ACD﹣45°=90°,
∴∠DHE=90°,
同(1)的方法得,MG⊥NG,
∴△MGN是等腰直角三角形.
一、选择题(共56分)
1.观察下列图案,既是轴对称图形又是中心对称图形的共有( )
A.4个 B.3个 C.2个 D.1个
2.下列因式分解中:①x3+2xy+x=x(x+2y);②x2+4x+4=(x+2)2;③﹣x2+y2=(x+y)(y﹣x);④x3﹣9x=x(x﹣3)2,正确的个数为( )
A.1个 B.2个 C.3个 D.4个
3.若正多边形的内角和是1080°,则该正多边形的一个外角为( )
A.45° B.60° C.72° D.90°
4.在四边形ABCD中,O是对角线交点,下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AD∥BC,AD=BC B.AB=DC,AD=BC
C.AB∥DC,AD=BC D.OA=OC,OD=OB
5.如图,在平行四边形ABCD中,AB=4,BC=6,对角线AC、BD相交于点O,则OA的取值范围是( )
A.2<OA<10 B.1<OA<5 C.4<OA<6 D.2<OA<8
6.下列各分式中,是最简分式的是( )
A. B. C. D.
7.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )
A.70° B.65° C.60° D.55°
8.某校为了丰富学生的校园生活,准备购进一批篮球和足球,其中篮球的单价比足球的单价多20元.李老师购买篮球花费900元,购买足球花费400元,结果购得的篮球数量是足球数量的1.5倍.设购买的足球数量是x个,则下列选项中所列方程正确的是( )
A.=+20 B.=+20
C.=+20 D.=+20
9.关于x的分式方程有增根,则m的值为( )
A.2 B.3 C.4 D.5
10.对于一组统计数据3,3,6,5,3.下列说法错误的是( )
A.众数是3 B.平均数是4 C.方差是1.6 D.中位数是6
11.在 ABCD中,EF过对角线的交点O,AB=4,BC=5,OF=1.5,则四边形ABFE的周长是( )
A.11 B.11.5 C.12 D.12.5
12.若关于x的分式方程=1的解为正数,且关于y的不等式组至少两个整数解,则符合条件的所有整数m的取值之和为( )
A.﹣7 B.﹣9 C.﹣12 D.﹣14
13.如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )
A.14 B.16 C.18 D.20
14.如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )
A. B.2 C. D.3
二、填空题(共32分.)
15.因式分解:m3﹣6m2+9m= .
16.在平行四边形ABCD中,AD=BD,BE是AD边上的高,∠EBD=10°,则∠A的度数为 .
17.如图,直线AE∥BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
18.如图,△ABC的边长AB=3cm,BC=4cm,AC=2cm,将△ABC沿BC方向平移acm(a<4),得到△DEF,连接AD,则阴影部分的周长为 cm.
19.已知a+b=5,ab=3,则代数式a3b+2a2b2+ab3= .
20.若分式的值为0,则x= .
21.在平面直角坐标系中,点A(﹣5,b)关于原点对称的点为B(a,6),则(a+b)2022= .
22.如图,长方形ABCD的两边BC,CD分别在x轴、y轴上,点C与原点重合,点A(﹣1,2),将长方形ABCD沿x轴无滑动向右翻滚,经过一次翻滚,点A对应点记为A1;经过第二次翻滚,点A对应点记为A2;…;依此类推,经过第2020次翻滚,点A对应点A2020坐标为 .
三、解答题(共62分)
23.先化简,再求值:÷+,其中a=.
24.为弘扬泰山文化,我市某校举办了“泰山诗文大赛”活动,小学、初中部根据初赛成绩,各选出5名选手组成小学代表队和初中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩(满分为100分)如图所示.
(1)根据图示填写图表;
平均数(分) 中位数(分) 众数(分)
小学部 85
初中部 85 100
(2)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
25.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无需说明理由)
26.如图①,平行四边形ABCD的对角线AC,BD相交于点O,EF过点O与AB,CD分别相交于点E,F.
(1)求证:BE=DF;
(2)若图中的条件都不变,将EF转动到图②的位置,那么上述结论是否成立?说明理由.
27.某个体经营户了解到有一种盒装商品能畅销市场,就用4万元购进这种商品,面市后果然供不应求,他又用8.8万元购进了第二批这种商品,所购数量是第一批购进量的2倍,但每盒单价涨了4元,他在销售这种盒装商品时每盒定价都是56元,最后剩下的150盒按八折销售,很快售完,在这两笔生意中,这位个体经营户共赢利多少元?
28.(1)操作发现:如图①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是 ;位置关系是 .
(2)类比思考:
如图②,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其它条件不变,小明发现的上述结论还成立吗?请说明理由.
(3)深入研究:
如图③,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其它条件不变,试判断△GMN的形状,并给与证明.
参考答案
选择题(共56分)
1.解:第1个是轴对称图形,不是中心对称图形,故此选项不合题意;
第2个是轴对称图形,也是中心对称图形,故此选项符合题意;
第3个是轴对称图形,也是中心对称图形,故此选项符合题意;
第4个不是轴对称图形,是中心对称图形,故此选项不合题意.
故选:C.
2.解:①x3+2xy+x=x(x2+2y+1),故原题分解错误;
②x2+4x+4=(x+2)2,故原题分解正确;
③﹣x2+y2=y2﹣x2=(x+y)(y﹣x),故原题分解正确;
④x3﹣9x=x(x2﹣9)=x(x+3)(x﹣3),故原题分解错误;
正确的个数为2个,
故选:B.
3.解:设这个正多边形的边数为n,
∵一个正多边形的内角和为1080°,
∴180(n﹣2)=1080,
解得:n=8,
∴这个正多边形的每一个外角是:360°÷8=45°.
故选:A.
4.解:A、根据一组对边平行且相等的四边形是平行四边形,可以判定,故正确;
B、根据平行四边形的定义即可判定,故正确;
C、一组对边平行,另一组对边相等的四边形,等腰梯形满足条件.故该选项错误.
D、根据对角线互相平分的四边形是平行四边形可以判定.故正确.
故选:C.
5.解:∵AB=4,BC=6,
∴2<AC<10,
∵四边形ABCD是平行四边形,
∴AO=AC,
∴1<OA<5,
故选:B.
6.解:A.是最简分式;
B.==x﹣y,不符合题意;
C.==,不符合题意;
D.=,不符合题意;
故选:A.
7.解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,
∴AC=A′C,
∴△ACA′是等腰直角三角形,
∴∠CAA′=45°,
∴∠A′B′C=∠1+∠CAA′=20°+45°=65°,
由旋转的性质得∠B=∠A′B′C=65°.
故选:B.
8.解:设购买的足球数量是x个,则购买篮球数量是1.5x个,
根据题意,得=+20.
故选:C.
9.解:去分母得5x+3(x﹣1)=2m+1,
解得x=,
因为原方程的增根为x=1,
所以=1,解得m=2,
即m=2时,分式方程有增根.
故选:A.
10.解:将这组数据重新排列为3、3、3、5、6,
∴这组数据的众数为3,
平均数为=4,
方差为×[3×(3﹣4)2+(5﹣4)2+(6﹣4)2]=1.6,
中位数为3,
故选:D.
11.解:已知AB=4,BC=5,OE=1.5,
根据平行四边形的性质,AB=CD=4,BC=AD=5,
在△AEO和△CFO中OA=OC,∠OAE=∠OCF,∠AOE=∠COF,
所以△AEO≌△CFO,OE=OF=1.5,
则ABFE的周长=EFCD的周长=ED+CD+CF+EF=(DE+CF)+AB+EF=5+4+3=12.
故选:C.
12.解:由方程=1,解得:x=﹣2﹣m,
则
可得:m<﹣2且m≠﹣5,
由①知,y>﹣2,
由②知,y≤,
∵关于y的不等式组至少两个整数解,
∴y=﹣1和0
∴5+m≥0,
解得:m≥﹣5,
所以m的整数值为﹣4,﹣3,
﹣4+(﹣3)=﹣7,
故选:A.
13.解:∵线段AB平移得到线段CD,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵A(1,0),B(4,0),
∴AB=4﹣1=3,
∵四边形ABCD的面积为9,
∴3 OC=9,
解得OC=3,
在Rt△BOC中,由勾股定理得,BC===5,
∴四边形ABCD的周长=2(3+5)=16.
故选:B.
14.解:∵BN平分∠ABC,BN⊥AE,
∴∠NBA=∠NBE,∠BNA=∠BNE,
在△BNA和△BNE中,
∴△BNA≌△BNE,
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点N是AE中点,点M是AD中点(三线合一),
∴MN是△ADE的中位线,
∵BE+CD=AB+AC=19﹣BC=19﹣7=12,
∴DE=BE+CD﹣BC=5,
∴MN=DE=.
故选:C.
二、填空题(共32分.)
15.解:m3﹣6m2+9m=m(m2﹣6m+9)=m(m﹣3)2,
故答案为:m(m﹣3)2.
16.解:情形一:当E点在线段AD上时,如图所示,
∵BE是AD边上的高,∠EBD=10°,
∴∠ADB=90°﹣10°=80°,
∵AD=BD,
∴∠A=∠ABD=(180°﹣80°)÷2=50°;
情形二:当E点在AD的延长线上时,如图所示,
∵BE是AD边上的高,∠EBD=10°,
∴∠BDE=80°,
∵AD=BD,
∴∠A=∠ABD=∠BDE=40°.
故答案为:50°或40°.
17.解:过点A作AF⊥BD于点F,
∵△ABD的面积为16,BD=8,
∴BD AF=×8×AF=16,
解得AF=4,
∵AE∥BD,
∴AF的长是△ACE的高,
∴S△ACE=×AE×4=×5×4=10.
故答案为:10.
18.解:∵将△ABC沿BC方向平移acm(a<4cm),得到△DEF,
∴AD=BE,AB=DE,AC=DF,
∴阴影部分的周长=AD+EC+DE+AC=BE+EC+AC+AB=AB+AC+BC=3+4+2=9cm,
故答案为:9.
19.解:原式=ab(a2+2ab+b2)=ab(a+b)2,
当a+b=5,ab=3时,原式=3×52=75.
故答案是:75.
20.解:∵x2﹣4=0,
∴x=±2,
当x=2时,x+2≠0,
当x=﹣2时,x+2=0.
∴当x=2时,分式的值是0.
故答案为:2.
21.解:∵点A(﹣5,b)关于原点对称的点为B(a,6),
∴a=5,b=﹣6,
则(a+b)2022=(5﹣6)2022=1.
故答案为:1.
22.解:如图所示:
观察图形可得经过4次翻滚后点A对应点一循环,
2020÷4=505,
∵点A(﹣1,2),长方形的周长为:2(1+2)=6,
∴经过505次翻滚后点A对应点A2020的坐标为(6×505﹣1,2),即(3029,2).
故答案为:(3029,2).
三、解答题(共62分)
23.解:原式=[+]×+
=×==,
把a=代入得,
原式==.
24.解:(1)填表:小学部平均数:(75+80+85+85+100)÷5=85(分);
小学部得分中85出现的次数最多,则小学部的众数为85分;
初中部得分情况为70,75,80,100,100,则初中部的中位数为80分.
(2)∵=[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,,
∴,
因此,小学代表队选手成绩较为稳定.
25.解:(1)如图所示,△A1B1C1即为所求:
(2)如图所示,△A2B2C2即为所求:
(3)三角形的形状为等腰直角三角形,OB=OA1=,A1B=,
即,
所以三角形的形状为等腰直角三角形.
26.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OB=OD,
∴∠OBE=∠ODF,
在△OBE和△ODF中,
,
∴△OBE≌△ODF(ASA),
∴BE=DF;
(2)解:结论成立,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,OB=OD,
∴∠OAE=∠OCF,∠OEF=∠OFC
在△OAE和△OCF中,
,
∴△OAE≌△OCF(AAS),
∴OE=OF,
在△OBE和△ODF中,
,
∴△OBE≌△ODF(SAS),
∴BE=DF.
27.解:设第一批进货的单价为x元,则第二批进货的单价为(x+4)元,依题意有
×2=,
解得:x=40,
经检验x=40是原分式方程的解,且符合题意,
则第一次进货1000件,
第二次进货的单价为44元,第二次进货2000件,
总盈利为:(56﹣40)×1000+(56﹣44)×(2000﹣150)+150×(56×0.8﹣44)
=16000+22200+120
=38320(元).
答:这位个体经营户共赢利38320元.
28.解:(1)如图①,连接BE,CD相交于H,
∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AC=AE,∠BAD=∠CAE=90°
∴∠CAD=∠BAE,
∴△ACD≌△AEB(SAS),
∴CD=BE,∠ADC=∠ABE,
∴∠BDC+∠DBH=∠BDC+∠ABD+∠ABE=∠BDC+∠ABD+∠ADC=∠ADB+∠ABD=90°,
∴∠BHD=90°,
∴CD⊥BE,
∵点M,G分别是BD,BC的中点,
∴MGCD,
同理:NGBE,
∴MG=NG,MG⊥NG,
故答案为:MG=NG,MG⊥NG;
(2)如图②,连接CD,BE相交于点H,
同(1)的方法得,MG=NG,MG⊥NG;
(3)如图③,连接EB,DC,延长线相交于H,
同(1)的方法得,MG=NG,
同(1)的方法得,△ABE≌△ADC,
∴∠AEB=∠ACD,
∴∠CEH+∠ECH=∠AEH﹣∠AEC+180°﹣∠ACD﹣∠ACE=∠ACD﹣45°+180°﹣∠ACD﹣45°=90°,
∴∠DHE=90°,
同(1)的方法得,MG⊥NG,
∴△MGN是等腰直角三角形.
同课章节目录
