椭圆的定义及标准方程1[上学期]
文档属性
| 名称 | 椭圆的定义及标准方程1[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 835.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-09-24 00:00:00 | ||
图片预览











文档简介
课件36张PPT。引言 第二章
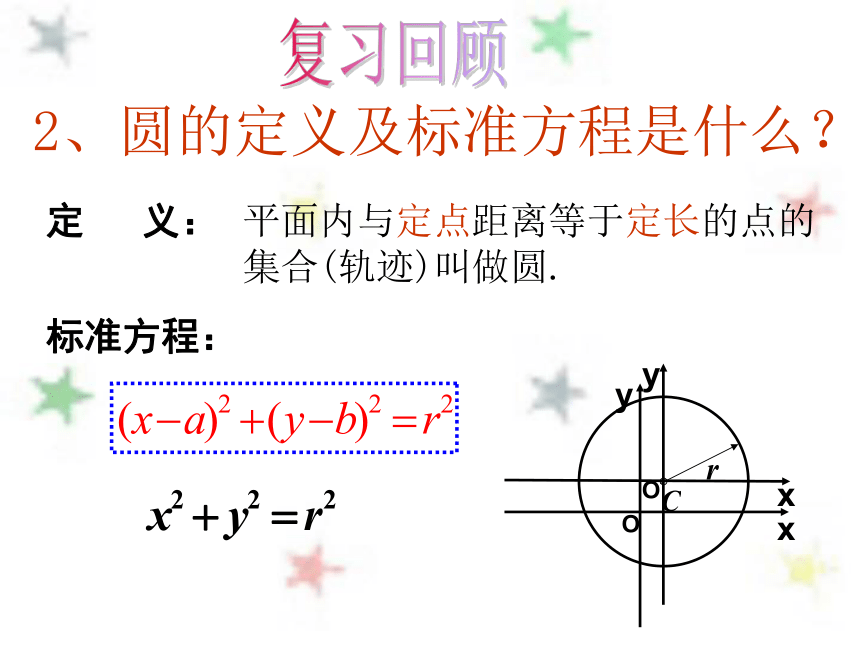
圆锥曲线与方程相 框丰田汽车标志北宋 汝窑天青无文椭圆水仙盆 玉 石 神州六号搭乘两名航天员从酒泉卫星发射中心发射升空,运行在轨道倾角42.4度,近地点高度200千米,远地点高度347千米的椭圆轨道上运行了5圈。 行星运行的轨道(演示)2.2.1 椭圆及标准方程2.2 椭圆复习回顾 1、研究圆的方法:坐标法,利用圆的方程来定量地研究圆的性质.平面内与定点距离等于定长的点的
集合(轨迹)叫做圆.复习回顾标准方程:定 义:2、圆的定义及标准方程是什么?圆是与一定点的距离等于定长的点的集合。那么,椭圆又是什么样的点的集合?
椭圆的标准方程又是什么呢?新课导入我们来做一个实验:
取一条定长L的细绳,把它的两端固定在图板
的同一点处,套上铅笔,拉紧绳子,移动笔尖,
这时笔尖(动点)画出的轨迹是什么图形? 如果把细绳的两端拉开一段距离分别固定
在图板的两点处,套上铅笔,拉紧绳子,移动笔尖,
画出的是什么图形?几何画板演示2 平面内与两定点的距离之和等于
常数 的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点两焦点间的距离叫做椭圆的焦距椭圆的定义思考 知道了它的定义也就知道了椭圆的基本几何特征.但是,这只是一种“定性”的描述。
为了”定量”地研究椭圆
需要利用椭圆的方程,那
么如何求椭圆的方程呢?建立适当的坐标系,用有序实数对表示曲线上任意一点M的坐标.写出曲线上动点M适合的条件p的集合P={M|p(M)}用坐标表示条件p(M),列出方程f(x,y)=0化方程f(x,y)=0为最简形式回顾:求曲线方程的一般方法椭圆的标准方程建系、设点、列式、化简、证明证明方程为满足条件的方程一 建立直角坐标系求椭圆的标准方程思考?怎样建立坐标系才能使椭圆的方程简单?(1)(2)(3)(4)(5)(6) 建系的一般原则为:使已知点的坐标和曲线的方程尽可能简单,即原点取在定点或定线段的中点,坐标轴取在定直线上或图形的对称轴上,充分利用图形的对称性.建系的一般原则求椭圆的标准方程 设M(x,y)是椭圆上任意一点由椭圆的定义化简得思考?观察右图,你能从中找出
表示a,c, 的线段么?由椭圆的定义可知,2a>2c 即 a>c所以令代入上式得两边同时除以得焦点坐标其中焦点坐标其中椭圆的标准方程焦点在
x轴上焦点在
y轴上练习1指出在下列方程中,哪些是椭圆的标准方程?哪些是椭圆的方程。 练习2比较椭圆的两种标准方程并填表焦点在大数对应的轴上写出适合下列条件的椭圆的标准方程练习3习题训练1 根据椭圆的方程填空例题讲解1、椭圆的定义(强调2a>|F1F2|)和椭圆的标
准方程 2、椭圆的标准方程有两种,注意区分 4、求椭圆标准方程的方法 小结3、根据椭圆标准方程判断焦点位置的方法 1、46页习题2.1 1、2
2、登录www.zhaobao.com搜集神舟5、6号
的运行椭圆轨道参数,求出相应椭圆的
标准方程
作业再见!!A例1 已知△ABC的一边BC固定,长为6,周长为16,
求顶点A的轨迹方程。.
以BC的中点为原点,BC所在的直线为x轴建立直角坐标系。 所以可设椭圆的标准方程为 :
例题讲解解:根据椭圆的定义知所求轨迹是椭圆,
且B、C为焦点∴所求椭圆的标准方程为:解:设点M的坐标为(x,y),点P的坐标为则例题讲解D辅助点法例题讲解练习1 平面内有两个定点的距离是8,写出到这两个定点的距离的和是10的点的轨迹方程。(1)判断:1)和是常数;2)常数大于两个定点之间的距离。故点的轨迹是椭圆。(2)取过两个定点的直线做 x 轴,它的线段垂直平分线做 y 轴,建立直角坐标系,从而保证方程是标准方程。(3)根据已知求出a、c,再推出a、b
写出椭圆的标准方程。习题训练习题训练第40页 练习3,4
圆锥曲线与方程相 框丰田汽车标志北宋 汝窑天青无文椭圆水仙盆 玉 石 神州六号搭乘两名航天员从酒泉卫星发射中心发射升空,运行在轨道倾角42.4度,近地点高度200千米,远地点高度347千米的椭圆轨道上运行了5圈。 行星运行的轨道(演示)2.2.1 椭圆及标准方程2.2 椭圆复习回顾 1、研究圆的方法:坐标法,利用圆的方程来定量地研究圆的性质.平面内与定点距离等于定长的点的
集合(轨迹)叫做圆.复习回顾标准方程:定 义:2、圆的定义及标准方程是什么?圆是与一定点的距离等于定长的点的集合。那么,椭圆又是什么样的点的集合?
椭圆的标准方程又是什么呢?新课导入我们来做一个实验:
取一条定长L的细绳,把它的两端固定在图板
的同一点处,套上铅笔,拉紧绳子,移动笔尖,
这时笔尖(动点)画出的轨迹是什么图形? 如果把细绳的两端拉开一段距离分别固定
在图板的两点处,套上铅笔,拉紧绳子,移动笔尖,
画出的是什么图形?几何画板演示2 平面内与两定点的距离之和等于
常数 的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点两焦点间的距离叫做椭圆的焦距椭圆的定义思考 知道了它的定义也就知道了椭圆的基本几何特征.但是,这只是一种“定性”的描述。
为了”定量”地研究椭圆
需要利用椭圆的方程,那
么如何求椭圆的方程呢?建立适当的坐标系,用有序实数对表示曲线上任意一点M的坐标.写出曲线上动点M适合的条件p的集合P={M|p(M)}用坐标表示条件p(M),列出方程f(x,y)=0化方程f(x,y)=0为最简形式回顾:求曲线方程的一般方法椭圆的标准方程建系、设点、列式、化简、证明证明方程为满足条件的方程一 建立直角坐标系求椭圆的标准方程思考?怎样建立坐标系才能使椭圆的方程简单?(1)(2)(3)(4)(5)(6) 建系的一般原则为:使已知点的坐标和曲线的方程尽可能简单,即原点取在定点或定线段的中点,坐标轴取在定直线上或图形的对称轴上,充分利用图形的对称性.建系的一般原则求椭圆的标准方程 设M(x,y)是椭圆上任意一点由椭圆的定义化简得思考?观察右图,你能从中找出
表示a,c, 的线段么?由椭圆的定义可知,2a>2c 即 a>c所以令代入上式得两边同时除以得焦点坐标其中焦点坐标其中椭圆的标准方程焦点在
x轴上焦点在
y轴上练习1指出在下列方程中,哪些是椭圆的标准方程?哪些是椭圆的方程。 练习2比较椭圆的两种标准方程并填表焦点在大数对应的轴上写出适合下列条件的椭圆的标准方程练习3习题训练1 根据椭圆的方程填空例题讲解1、椭圆的定义(强调2a>|F1F2|)和椭圆的标
准方程 2、椭圆的标准方程有两种,注意区分 4、求椭圆标准方程的方法 小结3、根据椭圆标准方程判断焦点位置的方法 1、46页习题2.1 1、2
2、登录www.zhaobao.com搜集神舟5、6号
的运行椭圆轨道参数,求出相应椭圆的
标准方程
作业再见!!A例1 已知△ABC的一边BC固定,长为6,周长为16,
求顶点A的轨迹方程。.
以BC的中点为原点,BC所在的直线为x轴建立直角坐标系。 所以可设椭圆的标准方程为 :
例题讲解解:根据椭圆的定义知所求轨迹是椭圆,
且B、C为焦点∴所求椭圆的标准方程为:解:设点M的坐标为(x,y),点P的坐标为则例题讲解D辅助点法例题讲解练习1 平面内有两个定点的距离是8,写出到这两个定点的距离的和是10的点的轨迹方程。(1)判断:1)和是常数;2)常数大于两个定点之间的距离。故点的轨迹是椭圆。(2)取过两个定点的直线做 x 轴,它的线段垂直平分线做 y 轴,建立直角坐标系,从而保证方程是标准方程。(3)根据已知求出a、c,再推出a、b
写出椭圆的标准方程。习题训练习题训练第40页 练习3,4
