椭圆[上学期]
图片预览







文档简介
课件20张PPT。椭圆及其标准方程绵竹中学数学组 观察做图过程(1)绳长应当大于F1、F2之间的距离。(2)由于绳长固定,所以 M 到两个定点的距离和也固定。数 学 实 验(1)取一条细绳,
(2)把它的两端固定在板上的两点F1、F2
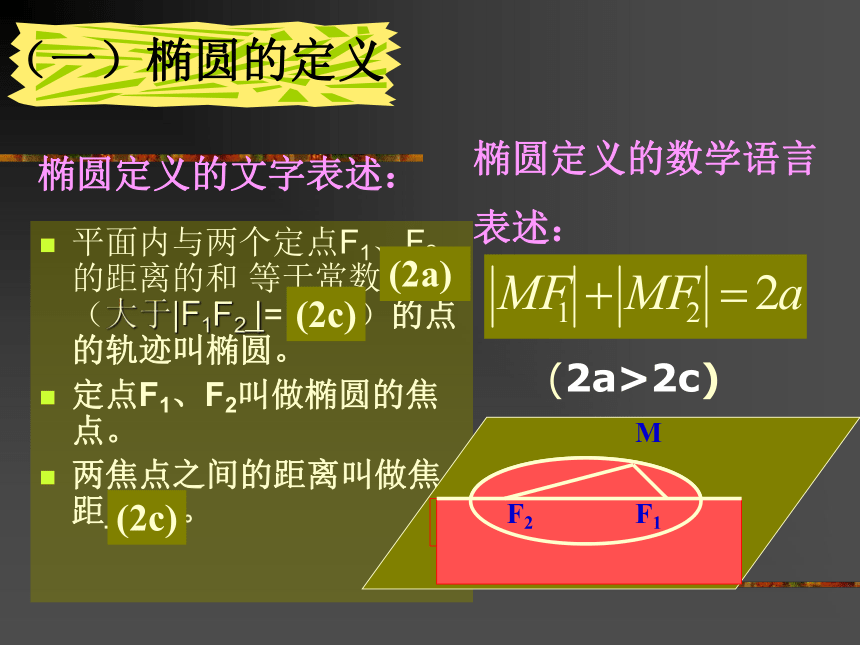
(3)用粉笔尖(M)把细绳拉紧,在板上慢慢移动看画出的 图形(一)椭圆的定义平面内与两个定点F1、F2的距离的和 等于常数___ (大于|F1F2 |= ___ )的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距__ 。椭圆定义的文字表述:椭圆定义的数学语言
表述:(2a>2c)MF2F1(2a)(2c)(2c) 基本步骤:
(1)建系设点
(2)表示集合
(3)列式
(4)化简
(5)证明椭圆方程的推导解:以焦点F1`F2所在直线为x轴,线段F1F2中点为坐标原点,建立平面直角坐标系,则F1(-c,0),F2(c,0)。设M(x, y)为椭圆上的任意一点,M与F1和F2的距离的和等于正常数2a。则 |MF1|+|MF2|=2a,即
将这个方程移项,两边平方,整理得两边再平方,得
a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2,
整理得 (a2-c2)x2+a2y2=a2(a2-c2),由椭圆的定义可知 2a>2c 即 a>c所以两边同时除以得椭圆的标准方程它表示:
(1)椭圆的焦点在x轴上
(2)焦点是F1(-C,0),F2(C,0)
(3)C2= a2 - b2 椭圆的标准方程它表示:
(1)椭圆的焦点在y轴上
(2)焦点是F1(0,-C),F2(0,C)
(3)C2= a2 - b2 F1F2M0xy椭圆的焦点在y轴上
焦点F1(0,-C),F2(0,C)
C2= a2 - b2 F1F2M0xy椭圆的焦点在x轴上
焦点F1(-C,0),F2(C,0)
C2= a2 - b2 焦点在X轴上时:焦点在Y轴上时:
给出椭圆标准方程怎样判断焦点在哪个轴上?结论:哪个项的分母大,焦点就在相应的那个变量轴上。反过来,焦点在哪个轴上,相应那个项的分母就大.∴所求椭圆的标准方程为根据已知求出a=___,c=___,再推出a、b=?设出椭圆的标准方程为用待定系数法求椭圆方程该选用哪种形式?
分析:54由焦点坐标知,点的轨迹是焦点在 x轴上的椭圆。(一)椭圆的定义平面内与两个定点F1、F2的距离的和 等于常数___ (大于|F1F2 |= ___ )的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距__ 。椭圆定义的文字表述:椭圆定义的数学语言表述:(2a>2c)MF2F1(2a)(2c)(2c)∴所求椭圆的标准方程为根据已知求出a=___,c=___,再推出a、b=?设出椭圆的标准方程为选取方程形式:由焦点坐标知,点的轨迹是焦点在 Y轴上的椭圆。分析:54∴椭圆的标准方程为根据已知求出a=___,c=___,再推出b.分别设出椭圆的标准方程为选取方程形式:由焦点距离可知2C=8,2a=10但不能确定椭圆的焦点在哪个 轴上。分析:54或或求椭圆方程的方法和步骤:①根据题意,设出标准方程。(由焦点的位置设出标准方程。)②根据条件确定a,b的值。③写出椭圆的方程。练习:96页练习3(1),(2)小结: (1)椭圆的定义: (2)标准方程的两种形式平面内与两个定点F1、F2的距离的和 等于常数2a(大于|F1F2 | )的点的轨迹叫椭圆。
想一想:(2)两个焦点的坐标分别是(-4,0)、(4,0)。轨迹上一点P到两焦点距离的和等于6?
小结: (1)椭圆的定义: (2)标准方程的两种形式平面内与两个定点F1、F2的距离的和 等于常数2a(大于|F1F2 | )的点的轨迹叫椭圆。
若2a=2c,则轨迹表示线段.
若2a<2c,则轨迹不存在。
椭圆的焦点在y轴上
焦点F1(0,-C),F2(0,C)
C2= a2 - b2 F1F2M0xy椭圆的焦点在x轴上
焦点F1(-C,0),F2(C,0)
C2= a2 - b2 焦点在X轴上时:焦点在Y轴上时:
作 业教材96页习题8.1:1. (2); .(3);
2.
3. (1) (3)(4)2005、10、11学习进步
再见!
(2)把它的两端固定在板上的两点F1、F2
(3)用粉笔尖(M)把细绳拉紧,在板上慢慢移动看画出的 图形(一)椭圆的定义平面内与两个定点F1、F2的距离的和 等于常数___ (大于|F1F2 |= ___ )的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距__ 。椭圆定义的文字表述:椭圆定义的数学语言
表述:(2a>2c)MF2F1(2a)(2c)(2c) 基本步骤:
(1)建系设点
(2)表示集合
(3)列式
(4)化简
(5)证明椭圆方程的推导解:以焦点F1`F2所在直线为x轴,线段F1F2中点为坐标原点,建立平面直角坐标系,则F1(-c,0),F2(c,0)。设M(x, y)为椭圆上的任意一点,M与F1和F2的距离的和等于正常数2a。则 |MF1|+|MF2|=2a,即
将这个方程移项,两边平方,整理得两边再平方,得
a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2,
整理得 (a2-c2)x2+a2y2=a2(a2-c2),由椭圆的定义可知 2a>2c 即 a>c所以两边同时除以得椭圆的标准方程它表示:
(1)椭圆的焦点在x轴上
(2)焦点是F1(-C,0),F2(C,0)
(3)C2= a2 - b2 椭圆的标准方程它表示:
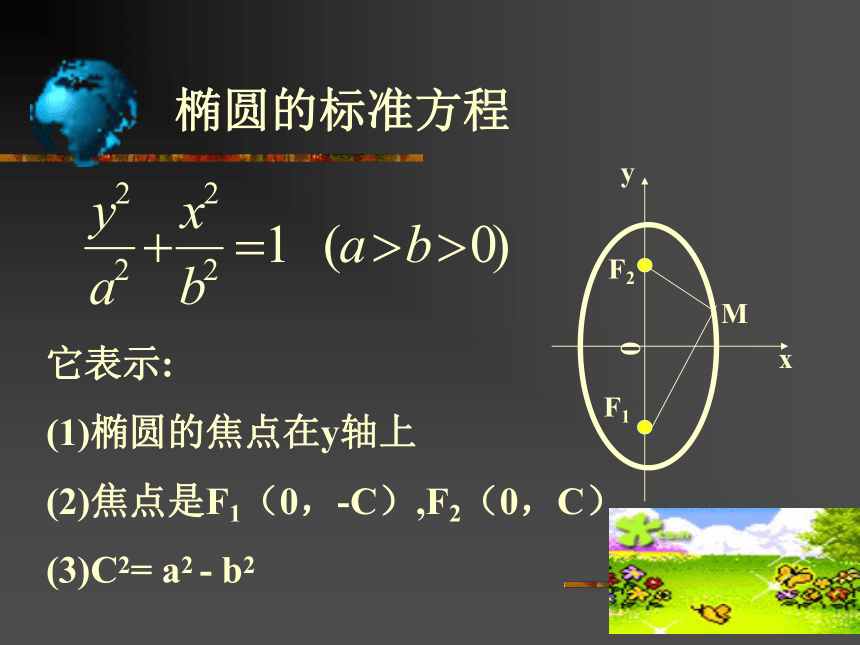
(1)椭圆的焦点在y轴上
(2)焦点是F1(0,-C),F2(0,C)
(3)C2= a2 - b2 F1F2M0xy椭圆的焦点在y轴上
焦点F1(0,-C),F2(0,C)
C2= a2 - b2 F1F2M0xy椭圆的焦点在x轴上
焦点F1(-C,0),F2(C,0)
C2= a2 - b2 焦点在X轴上时:焦点在Y轴上时:
给出椭圆标准方程怎样判断焦点在哪个轴上?结论:哪个项的分母大,焦点就在相应的那个变量轴上。反过来,焦点在哪个轴上,相应那个项的分母就大.∴所求椭圆的标准方程为根据已知求出a=___,c=___,再推出a、b=?设出椭圆的标准方程为用待定系数法求椭圆方程该选用哪种形式?
分析:54由焦点坐标知,点的轨迹是焦点在 x轴上的椭圆。(一)椭圆的定义平面内与两个定点F1、F2的距离的和 等于常数___ (大于|F1F2 |= ___ )的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距__ 。椭圆定义的文字表述:椭圆定义的数学语言表述:(2a>2c)MF2F1(2a)(2c)(2c)∴所求椭圆的标准方程为根据已知求出a=___,c=___,再推出a、b=?设出椭圆的标准方程为选取方程形式:由焦点坐标知,点的轨迹是焦点在 Y轴上的椭圆。分析:54∴椭圆的标准方程为根据已知求出a=___,c=___,再推出b.分别设出椭圆的标准方程为选取方程形式:由焦点距离可知2C=8,2a=10但不能确定椭圆的焦点在哪个 轴上。分析:54或或求椭圆方程的方法和步骤:①根据题意,设出标准方程。(由焦点的位置设出标准方程。)②根据条件确定a,b的值。③写出椭圆的方程。练习:96页练习3(1),(2)小结: (1)椭圆的定义: (2)标准方程的两种形式平面内与两个定点F1、F2的距离的和 等于常数2a(大于|F1F2 | )的点的轨迹叫椭圆。
想一想:(2)两个焦点的坐标分别是(-4,0)、(4,0)。轨迹上一点P到两焦点距离的和等于6?
小结: (1)椭圆的定义: (2)标准方程的两种形式平面内与两个定点F1、F2的距离的和 等于常数2a(大于|F1F2 | )的点的轨迹叫椭圆。
若2a=2c,则轨迹表示线段.
若2a<2c,则轨迹不存在。
椭圆的焦点在y轴上
焦点F1(0,-C),F2(0,C)
C2= a2 - b2 F1F2M0xy椭圆的焦点在x轴上
焦点F1(-C,0),F2(C,0)
C2= a2 - b2 焦点在X轴上时:焦点在Y轴上时:
作 业教材96页习题8.1:1. (2); .(3);
2.
3. (1) (3)(4)2005、10、11学习进步
再见!
