苏教版(2019)高中数学选择性必修第二册 6.1.1空间向量的线性运算(17张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第二册 6.1.1空间向量的线性运算(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 472.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 09:10:50 | ||
图片预览

文档简介
(共17张PPT)
6.1.1 空间向量的线性运算
学习目标
1. 了解空间向量概念,理解与平面向量异同
2. 掌握空间向量加法减法数乘运算
3. 掌握两向量共线定理
情景引入
复习引入
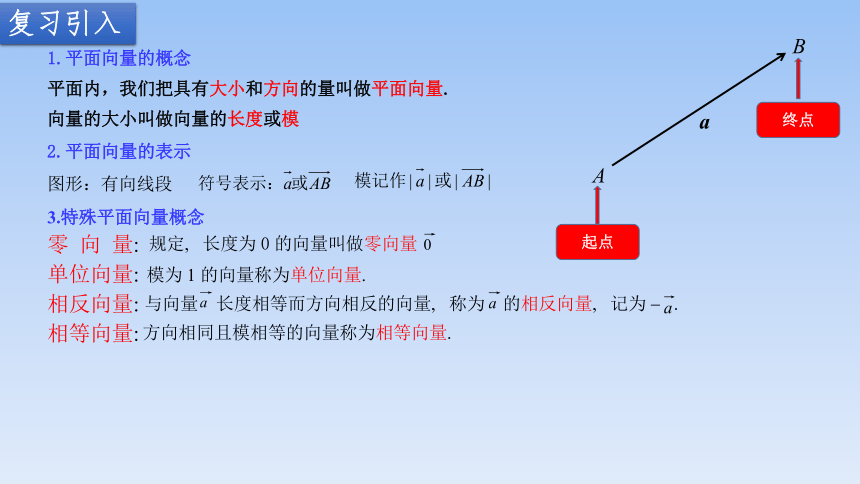
1.平面向量的概念
平面内,我们把具有大小和方向的量叫做平面向量.
向量的大小叫做向量的长度或模
2.平面向量的表示
图形:有向线段
A
B
a
起点
终点
3.特殊平面向量概念
零 向 量:
单位向量:
相反向量:
相等向量:
模为 1 的向量称为单位向量.
与向量 长度相等而方向相反的向量, 称为 的相反向量, 记为 - .
方向相同且模相等的向量称为相等向量.
规定, 长度为 0 的向量叫做零向量
复习引入
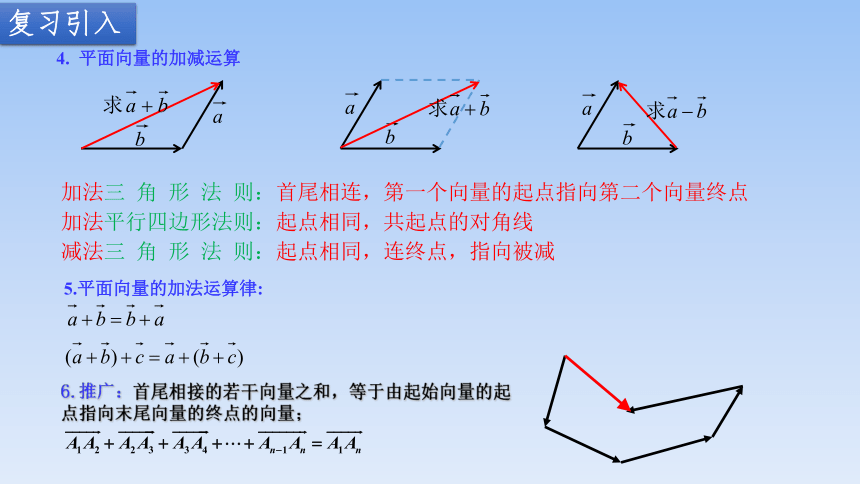
4. 平面向量的加减运算
加法三 角 形 法 则:首尾相连,第一个向量的起点指向第二个向量终点
加法平行四边形法则:起点相同,共起点的对角线
减法三 角 形 法 则:起点相同,连终点,指向被减
6.推广:首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量;
5.平面向量的加法运算律:
情景引入
正东
正北
向上
F1
F2
F3
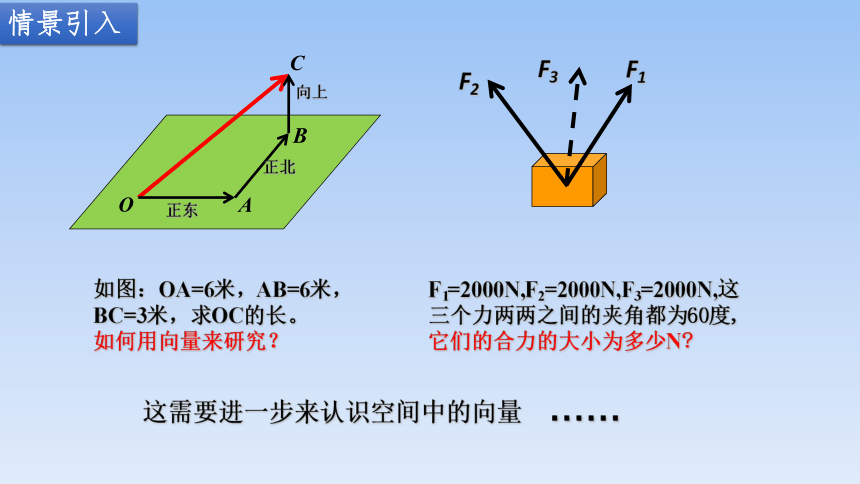
F1=2000N,F2=2000N,F3=2000N,这三个力两两之间的夹角都为60度,它们的合力的大小为多少N
这需要进一步来认识空间中的向量
……
如图:OA=6米,AB=6米,BC=3米,求OC的长。
如何用向量来研究?
活动探究
A1
B
C
A
D
B1
C1
D1
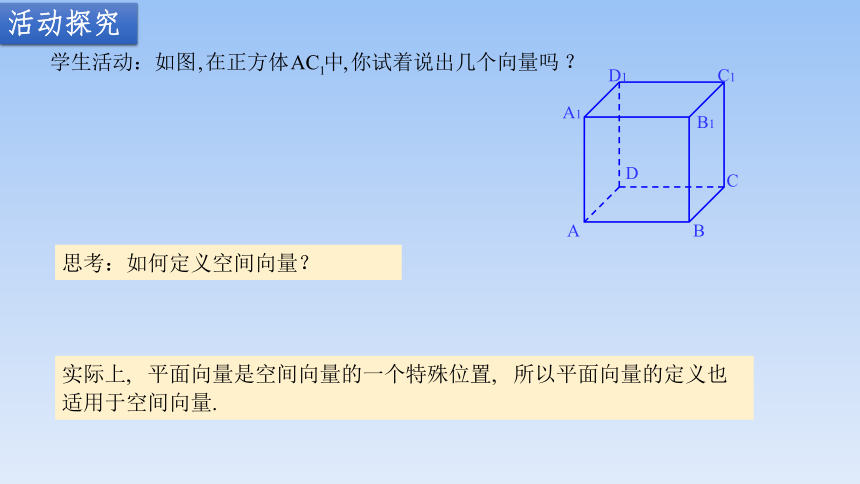
实际上, 平面向量是空间向量的一个特殊位置, 所以平面向量的定义也适用于空间向量.
思考:如何定义空间向量?
数学建构
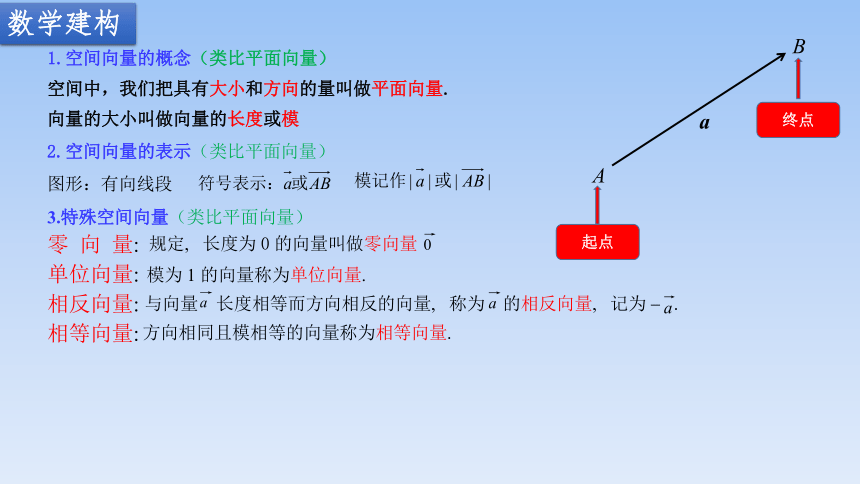
1.空间向量的概念(类比平面向量)
空间中,我们把具有大小和方向的量叫做平面向量.
向量的大小叫做向量的长度或模
2.空间向量的表示(类比平面向量)
图形:有向线段
A
B
a
起点
终点
3.特殊空间向量(类比平面向量)
零 向 量:
单位向量:
相反向量:
相等向量:
模为 1 的向量称为单位向量.
与向量 长度相等而方向相反的向量, 称为 的相反向量, 记为 - .
方向相同且模相等的向量称为相等向量.
规定, 长度为 0 的向量叫做零向量
活动探究
A1
B
C
A
D
B1
C1
D1
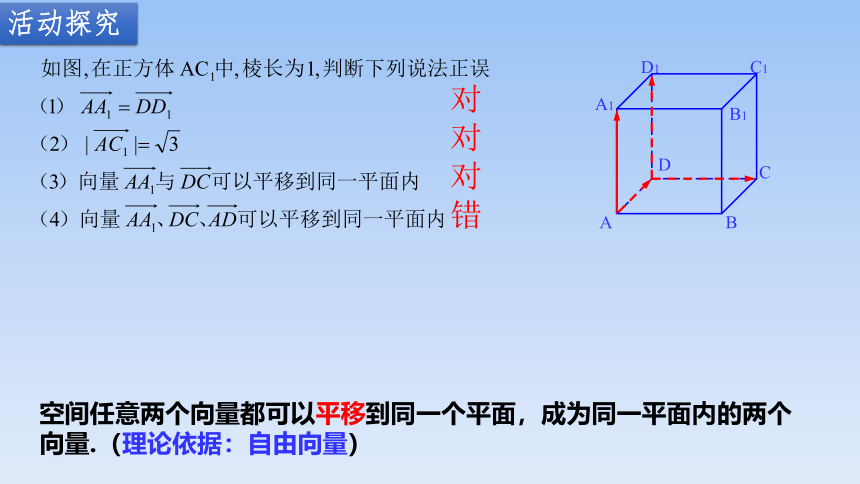
空间任意两个向量都可以平移到同一个平面,成为同一平面内的两个向量.(理论依据:自由向量)
对
对
对
错
情景引入
A1
B
C
A
D
B1
C1
D1
对
对
对
错
对
对
第一步、平移到同一个平面,成为同一平面内的两个向量.
思考:怎样进行空间两向量的加法减法运算?
第二步、平面内运用三角形法则和平行四边形法则即可
数学建构
第一步、平移到同一个平面,成为同一平面内的两个向量.
1.空间两向量的加法减法运算
第二步、平面内运用三角形法则和平行四边形法则即可
2.空间向量的加法运算也满足交换律及结合律:
数学应用
A
B
C
D
A
B
C
D
例1. 如图, 在平行六面体 ABCD-A B C D 中, 分别标 出 表示的向量.
解:
同起点的不共面三个向量的和, 等于以这三个向量为棱的平行六面体的对角线向量, 起点与这三个向量的起点相同.
例2. 如图, 在平行六面体 ABCD-A B C D 中,用 表示 及
A
B
C
D
A
B
C
D
解:
数学应用
变1. 如图, 已知平行六面体 ABCD-A B C D , 化简下列各表达式, 并在图中标出化简结果的向量:
(1) (2)
(3) (4)
A
B
C
D
A
B
C
D
解:
(1)
(2)
数学应用
变1. 如图, 已知平行六面体 ABCD-A B C D , 化简下列各表达式, 并在图中标出化简结果的向量:
(1) (2)
(3) (4)
A
B
C
D
A
B
C
D
解:
(3)
(E为CC 的中点).
E
数学应用
A
B
C
D
A
B
C
D
解:
变1. 如图, 已知平行六面体 ABCD-A B C D , 化简下列各表达式, 并在图中标出化简结果的向量:
(1) (2)
(3) (4)
(4)
F
数学应用
数学建构
1.数乘定义(类比平面向量)
实数 l 与空间向量 a 的乘积 la仍然是一个向量, 称为向量的数乘运算.
如:
a
A
B
3a
C
D
2a
2.空间向量的数乘运算满足分配律及结合律.
分配律: l(a+b)=la+lb,
结合律: l(ma)=(lm)a.
-2a
当 l>0 时, la 与向量 a 方向相同; la 的长度是 a 的长度的 |l| 倍.
当 l<0 时, la 与向量 a 方向相反; la 的长度是 a 的长度的 |l| 倍.
当 l=0 时, la为零向量.
3.共线向量定理
向量 a//b 的充要条件是存在实数 l, 使a=lb.(b≠0)
数学建构
变2. 如图, 已知正方体ABCD-A B C D , 点 E, F分别是上底面AC和侧面CD的中心. 求下列各式中 x, y 的值:
(1)
(2)
(3)
A
B
C
D
A
B
C
D
E
F
解:
(1)
∴x=1.
(2)
(3)
课堂小结
比较 空间向量 平面向量
定义 相同 相同
加法 平移到共面 三角形、平行四边形法则
减法 平移到共面 三角形法则
数乘 相同 相同
共线定理 相同 相同
数量积
垂直
坐标表示
6.1.1 空间向量的线性运算
学习目标
1. 了解空间向量概念,理解与平面向量异同
2. 掌握空间向量加法减法数乘运算
3. 掌握两向量共线定理
情景引入
复习引入
1.平面向量的概念
平面内,我们把具有大小和方向的量叫做平面向量.
向量的大小叫做向量的长度或模
2.平面向量的表示
图形:有向线段
A
B
a
起点
终点
3.特殊平面向量概念
零 向 量:
单位向量:
相反向量:
相等向量:
模为 1 的向量称为单位向量.
与向量 长度相等而方向相反的向量, 称为 的相反向量, 记为 - .
方向相同且模相等的向量称为相等向量.
规定, 长度为 0 的向量叫做零向量
复习引入
4. 平面向量的加减运算
加法三 角 形 法 则:首尾相连,第一个向量的起点指向第二个向量终点
加法平行四边形法则:起点相同,共起点的对角线
减法三 角 形 法 则:起点相同,连终点,指向被减
6.推广:首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量;
5.平面向量的加法运算律:
情景引入
正东
正北
向上
F1
F2
F3
F1=2000N,F2=2000N,F3=2000N,这三个力两两之间的夹角都为60度,它们的合力的大小为多少N
这需要进一步来认识空间中的向量
……
如图:OA=6米,AB=6米,BC=3米,求OC的长。
如何用向量来研究?
活动探究
A1
B
C
A
D
B1
C1
D1
实际上, 平面向量是空间向量的一个特殊位置, 所以平面向量的定义也适用于空间向量.
思考:如何定义空间向量?
数学建构
1.空间向量的概念(类比平面向量)
空间中,我们把具有大小和方向的量叫做平面向量.
向量的大小叫做向量的长度或模
2.空间向量的表示(类比平面向量)
图形:有向线段
A
B
a
起点
终点
3.特殊空间向量(类比平面向量)
零 向 量:
单位向量:
相反向量:
相等向量:
模为 1 的向量称为单位向量.
与向量 长度相等而方向相反的向量, 称为 的相反向量, 记为 - .
方向相同且模相等的向量称为相等向量.
规定, 长度为 0 的向量叫做零向量
活动探究
A1
B
C
A
D
B1
C1
D1
空间任意两个向量都可以平移到同一个平面,成为同一平面内的两个向量.(理论依据:自由向量)
对
对
对
错
情景引入
A1
B
C
A
D
B1
C1
D1
对
对
对
错
对
对
第一步、平移到同一个平面,成为同一平面内的两个向量.
思考:怎样进行空间两向量的加法减法运算?
第二步、平面内运用三角形法则和平行四边形法则即可
数学建构
第一步、平移到同一个平面,成为同一平面内的两个向量.
1.空间两向量的加法减法运算
第二步、平面内运用三角形法则和平行四边形法则即可
2.空间向量的加法运算也满足交换律及结合律:
数学应用
A
B
C
D
A
B
C
D
例1. 如图, 在平行六面体 ABCD-A B C D 中, 分别标 出 表示的向量.
解:
同起点的不共面三个向量的和, 等于以这三个向量为棱的平行六面体的对角线向量, 起点与这三个向量的起点相同.
例2. 如图, 在平行六面体 ABCD-A B C D 中,用 表示 及
A
B
C
D
A
B
C
D
解:
数学应用
变1. 如图, 已知平行六面体 ABCD-A B C D , 化简下列各表达式, 并在图中标出化简结果的向量:
(1) (2)
(3) (4)
A
B
C
D
A
B
C
D
解:
(1)
(2)
数学应用
变1. 如图, 已知平行六面体 ABCD-A B C D , 化简下列各表达式, 并在图中标出化简结果的向量:
(1) (2)
(3) (4)
A
B
C
D
A
B
C
D
解:
(3)
(E为CC 的中点).
E
数学应用
A
B
C
D
A
B
C
D
解:
变1. 如图, 已知平行六面体 ABCD-A B C D , 化简下列各表达式, 并在图中标出化简结果的向量:
(1) (2)
(3) (4)
(4)
F
数学应用
数学建构
1.数乘定义(类比平面向量)
实数 l 与空间向量 a 的乘积 la仍然是一个向量, 称为向量的数乘运算.
如:
a
A
B
3a
C
D
2a
2.空间向量的数乘运算满足分配律及结合律.
分配律: l(a+b)=la+lb,
结合律: l(ma)=(lm)a.
-2a
当 l>0 时, la 与向量 a 方向相同; la 的长度是 a 的长度的 |l| 倍.
当 l<0 时, la 与向量 a 方向相反; la 的长度是 a 的长度的 |l| 倍.
当 l=0 时, la为零向量.
3.共线向量定理
向量 a//b 的充要条件是存在实数 l, 使a=lb.(b≠0)
数学建构
变2. 如图, 已知正方体ABCD-A B C D , 点 E, F分别是上底面AC和侧面CD的中心. 求下列各式中 x, y 的值:
(1)
(2)
(3)
A
B
C
D
A
B
C
D
E
F
解:
(1)
∴x=1.
(2)
(3)
课堂小结
比较 空间向量 平面向量
定义 相同 相同
加法 平移到共面 三角形、平行四边形法则
减法 平移到共面 三角形法则
数乘 相同 相同
共线定理 相同 相同
数量积
垂直
坐标表示
