苏教版(2019)高中数学选择性必修第二册 6.1.2空间向量的数量积运算(24张PPT
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第二册 6.1.2空间向量的数量积运算(24张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 563.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 09:15:23 | ||
图片预览





文档简介
(共24张PPT)
6.1.2空间向量的数量积运算
学习目标
1.必备知识:掌握空间向量夹角的概念及其表示方法,掌握数量积的概念、性质和运算律;
2.关键能力:会用数量积去解决简单的夹角、模、垂直问题;
3.核心素养:直观想象、数学运算。
复习引入
O
B
A
1.平面向量的数量积
2.平面向量的夹角
3.数量积运算律
复习引入
A
B
C
D
M
N
A
B
C
D
M
N
复习引入
O
B
A
1.平面向量的数量积
2.平面向量的夹角
3.平面向量数量积的几何意义
C
D
E
复习引入
思考探究:
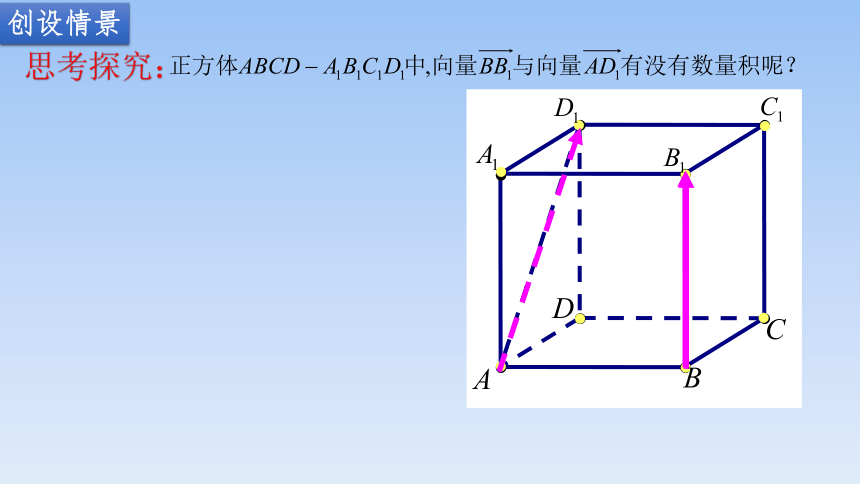
创设情景
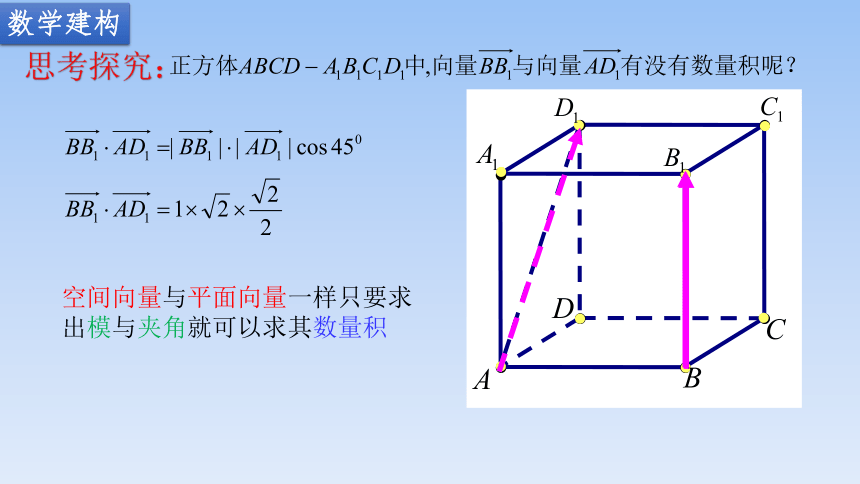
思考探究:
空间向量与平面向量一样只要求出模与夹角就可以求其数量积
数学建构
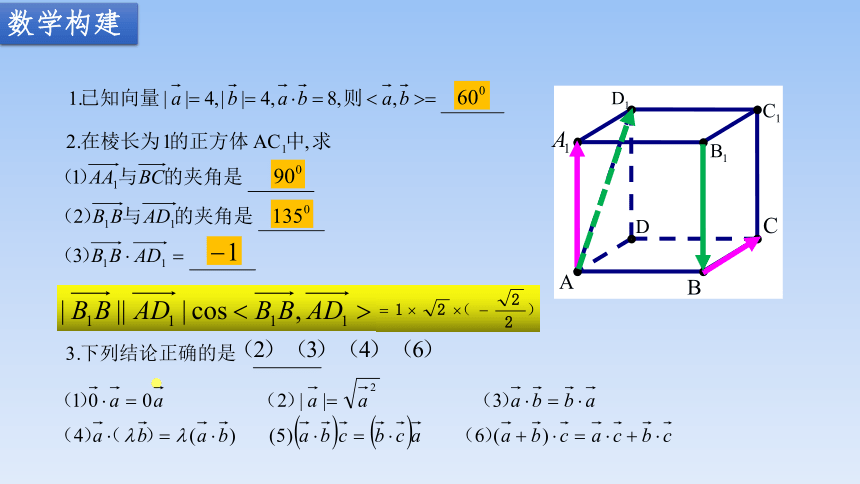
数学构建
O
A
B
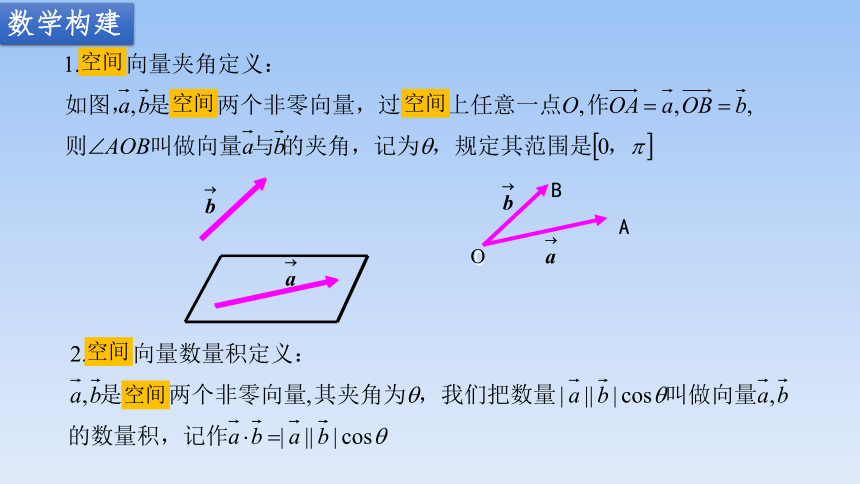
数学构建
O
B
A
1.空间向量的数量积
2.空间向量的夹角
5.空间向量的几何意义
A1
3.数量积运算律
4.向量垂直
数学构建
数量积的几何意义
向量在平面上的投影
数学应用
向量在平面上的投影
数学应用
数学应用
数学应用
练1. 在正三棱柱 ABC-A1B1C1中, 若 AB= BB1,则 AB1 与 C1B 所成角的大小为 ( )
(A) 60 (B) 90 (C) 105 (D) 75
A1
B1
C1
A
B
C
解:
设 BB1=a,
则
= 0,
得 AB1⊥C1B.
B
数学应用
练2. 如图, 在平行六面体 ABCD-A B C D 中, AB=4, AD=3, AA =5, ∠BAD=90 , ∠BAA =∠DAA =60 . 求 AC 的长.
A
B
C
D
A
B
C
D
解:
= 85,
数学应用
课堂小结
1.空间向量的数量积
空间向量的夹角
2.空间向量的投影向量
空间向量在直线上投影向量
空间向量在平面上投影向量
空间向量的模
锐角
钝角
直角
巩固提升
1. 如图, 已知空间四边形 ABCD 的每条边及AC, BD 的长都等于 a, 点 E, F, G 分别是 AB, AD, DC 的中点, 求:
(1) (2) (3)
(4) (5) (6)
A
B
C
D
E
F
G
解:
(1)
(2)
(3)
巩固提升
1. 如图, 已知空间四边形 ABCD 的每条边及AC, BD 的长都等于 a, 点 E, F, G 分别是 AB, AD, DC 的中点, 求:
(1) (2) (3)
(4) (5) (6)
A
B
C
D
E
F
G
解:
(4)
(5)
(6)
巩固提升
2. 如图, 在平行六面体 ABCD-A B C D 中, AB=5, AD=3, AA =7, ∠BAD=60 , ∠BAA =∠DAA =45 . 求 AC 的长.
A
B
C
D
A
B
C
D
解:
≈13.3.
巩固提升
3. 如图, 正方体ABCD-A B C D 的棱长为 a.
(1) 求A B和B C的夹角;(2) 求证: A B⊥AC .
A
B
C
D
A
B
C
D
解:
(1)
= a2,
即A B和B C的夹角为60 .
巩固提升
证明:
(2)
= 0,
∴A B⊥AC .
3. 如图, 正方体ABCD-A B C D 的棱长为 a.
(1) 求A B和B C的夹角;(2) 求证: A B⊥AC .
A
B
C
D
A
B
C
D
巩固提升
4. 如图, 已知空间四边形 OABC中, OA=OB, CA=CB, 点 E, F, G, H 分别是 OA, OB, BC, CA 的中点. 求证: 四边形 EFGH 是矩形.
A
B
C
O
E
F
G
H
证明:
∵ 点 E, F, G, H 分别是
OA, OB, BC, CA 的中点.
则
∴ EF//HG, 且 EF=HG,
得四边形EFGH是平行四边形.
又
①
∵ OA=OB, CA=CB,
得△OAC≌△OBC,
于是得
∴EF⊥FG.
由①②得四边形EFGH是矩形.
②
巩固提升
5. 如图, 线段 AB, BD 在平面 a 内, BD⊥AB, 线段 AC⊥a, 且 AB=a, BD=b, AC=c, 求 C, D 间的距离.
A
B
C
D
a
b
c
a
解:
6.1.2空间向量的数量积运算
学习目标
1.必备知识:掌握空间向量夹角的概念及其表示方法,掌握数量积的概念、性质和运算律;
2.关键能力:会用数量积去解决简单的夹角、模、垂直问题;
3.核心素养:直观想象、数学运算。
复习引入
O
B
A
1.平面向量的数量积
2.平面向量的夹角
3.数量积运算律
复习引入
A
B
C
D
M
N
A
B
C
D
M
N
复习引入
O
B
A
1.平面向量的数量积
2.平面向量的夹角
3.平面向量数量积的几何意义
C
D
E
复习引入
思考探究:
创设情景
思考探究:
空间向量与平面向量一样只要求出模与夹角就可以求其数量积
数学建构
数学构建
O
A
B
数学构建
O
B
A
1.空间向量的数量积
2.空间向量的夹角
5.空间向量的几何意义
A1
3.数量积运算律
4.向量垂直
数学构建
数量积的几何意义
向量在平面上的投影
数学应用
向量在平面上的投影
数学应用
数学应用
数学应用
练1. 在正三棱柱 ABC-A1B1C1中, 若 AB= BB1,则 AB1 与 C1B 所成角的大小为 ( )
(A) 60 (B) 90 (C) 105 (D) 75
A1
B1
C1
A
B
C
解:
设 BB1=a,
则
= 0,
得 AB1⊥C1B.
B
数学应用
练2. 如图, 在平行六面体 ABCD-A B C D 中, AB=4, AD=3, AA =5, ∠BAD=90 , ∠BAA =∠DAA =60 . 求 AC 的长.
A
B
C
D
A
B
C
D
解:
= 85,
数学应用
课堂小结
1.空间向量的数量积
空间向量的夹角
2.空间向量的投影向量
空间向量在直线上投影向量
空间向量在平面上投影向量
空间向量的模
锐角
钝角
直角
巩固提升
1. 如图, 已知空间四边形 ABCD 的每条边及AC, BD 的长都等于 a, 点 E, F, G 分别是 AB, AD, DC 的中点, 求:
(1) (2) (3)
(4) (5) (6)
A
B
C
D
E
F
G
解:
(1)
(2)
(3)
巩固提升
1. 如图, 已知空间四边形 ABCD 的每条边及AC, BD 的长都等于 a, 点 E, F, G 分别是 AB, AD, DC 的中点, 求:
(1) (2) (3)
(4) (5) (6)
A
B
C
D
E
F
G
解:
(4)
(5)
(6)
巩固提升
2. 如图, 在平行六面体 ABCD-A B C D 中, AB=5, AD=3, AA =7, ∠BAD=60 , ∠BAA =∠DAA =45 . 求 AC 的长.
A
B
C
D
A
B
C
D
解:
≈13.3.
巩固提升
3. 如图, 正方体ABCD-A B C D 的棱长为 a.
(1) 求A B和B C的夹角;(2) 求证: A B⊥AC .
A
B
C
D
A
B
C
D
解:
(1)
= a2,
即A B和B C的夹角为60 .
巩固提升
证明:
(2)
= 0,
∴A B⊥AC .
3. 如图, 正方体ABCD-A B C D 的棱长为 a.
(1) 求A B和B C的夹角;(2) 求证: A B⊥AC .
A
B
C
D
A
B
C
D
巩固提升
4. 如图, 已知空间四边形 OABC中, OA=OB, CA=CB, 点 E, F, G, H 分别是 OA, OB, BC, CA 的中点. 求证: 四边形 EFGH 是矩形.
A
B
C
O
E
F
G
H
证明:
∵ 点 E, F, G, H 分别是
OA, OB, BC, CA 的中点.
则
∴ EF//HG, 且 EF=HG,
得四边形EFGH是平行四边形.
又
①
∵ OA=OB, CA=CB,
得△OAC≌△OBC,
于是得
∴EF⊥FG.
由①②得四边形EFGH是矩形.
②
巩固提升
5. 如图, 线段 AB, BD 在平面 a 内, BD⊥AB, 线段 AC⊥a, 且 AB=a, BD=b, AC=c, 求 C, D 间的距离.
A
B
C
D
a
b
c
a
解:
