苏教版(2019)高中数学选择性必修第二册 6.1.3共面向量定理课件(15张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第二册 6.1.3共面向量定理课件(15张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 337.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
复习引入
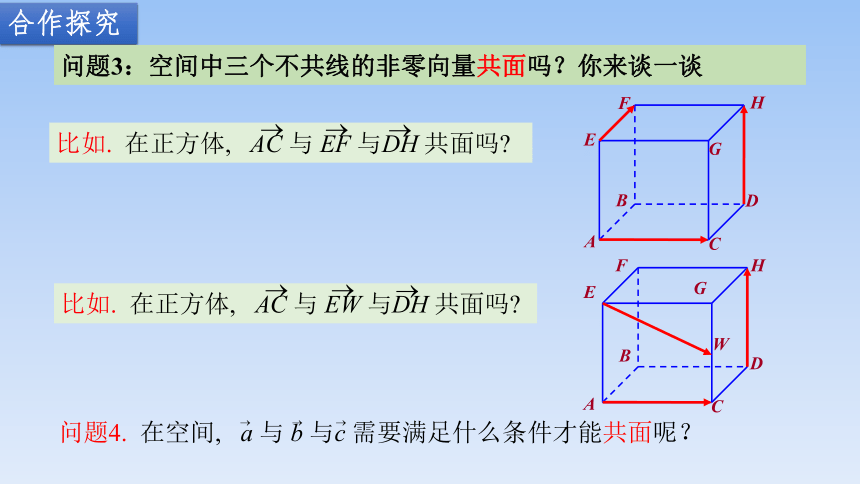
问题1:空间任意两向量是共线向量吗?你来谈一谈
图:
式:
可以平移到一条直线上
问题2:空间任意两向量是共面吗?你来谈一谈
空间任意两个向量都可以平移到同一个平面内,成为同一平面内的两个向量.
合作探究
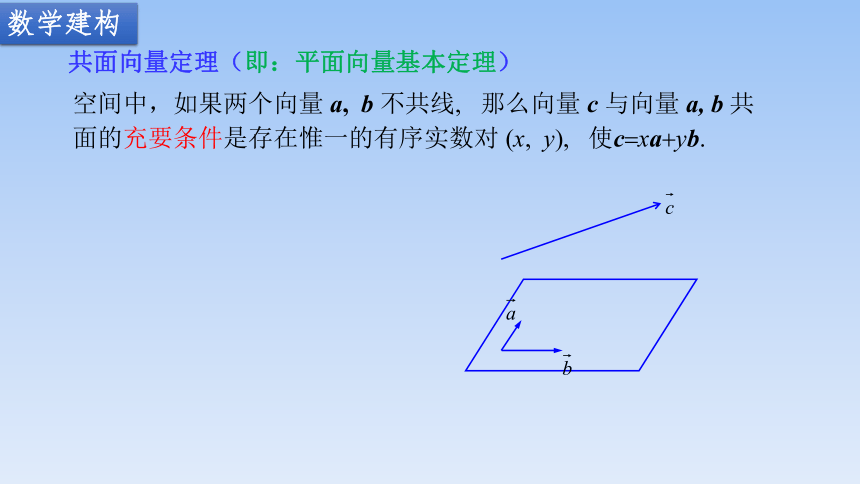
问题3:空间中三个不共线的非零向量共面吗?你来谈一谈
A
B
E
C
F
D
H
G
比如. 在正方体, AC 与 EF 与DH 共面吗
A
B
E
C
F
D
H
G
W
比如. 在正方体, AC 与 EW 与DH 共面吗
问题4. 在空间, a 与 b 与c 需要满足什么条件才能共面呢?
合作探究
问题4. 在空间, a 与 b 与c 需要满足什么条件才能共面呢?
平面内,如果两个向量 a, b 不共线, 那么向量 c 与向量 a, b 共面的充要条件是存在惟一的有序实数对 (x, y), 使c=xa+yb.
联想:平面向量的基本定理
空间中,如果两个向量 a, b 不共线, 那么向量 c 与向量 a, b 共面的充要条件是存在惟一的有序实数对 (x, y), 使c=xa+yb.
空间中这个定理还是用吗?
数学建构
空间中,如果两个向量 a, b 不共线, 那么向量 c 与向量 a, b 共面的充要条件是存在惟一的有序实数对 (x, y), 使c=xa+yb.
共面向量定理(即:平面向量基本定理)
数学应用
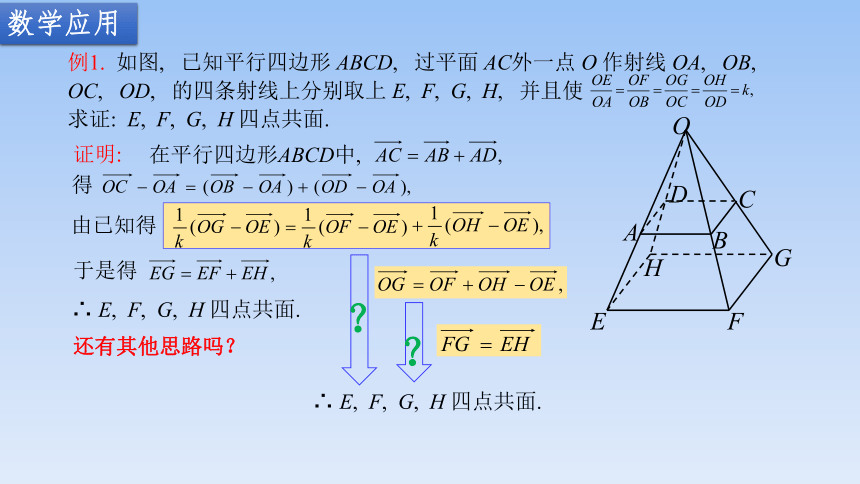
例1. 如图, 已知平行四边形 ABCD, 过平面 AC外一点 O 作射线 OA, OB, OC, OD, 的四条射线上分别取上 E, F, G, H, 并且使 求证: E, F, G, H 四点共面.
O
A
B
C
D
E
F
G
H
分析:
用 表示
用 表示
用 表示;
用 表示.
用 表示
用 表示
用 表示
而
数学应用
证明:
在平行四边形ABCD中,
得
由已知得
于是得
∴ E, F, G, H 四点共面.
O
A
B
C
D
E
F
G
H
例1. 如图, 已知平行四边形 ABCD, 过平面 AC外一点 O 作射线 OA, OB, OC, OD, 的四条射线上分别取上 E, F, G, H, 并且使 求证: E, F, G, H 四点共面.
还有其他思路吗?
∴ E, F, G, H 四点共面.
?
?
数学应用
O
A
B
C
D
E
F
G
H
变. 如图, 已知平行四边形 ABCD, 过平面 AC外一点 O 作射线 OA, OB, OC, OD, 的四条射线上分别取上 E, F, G, H, 并且使 求证: E, F, G, H 四点共面.
证明:
在平行四边形ABCD中,
得
由已知得
∴ E, F, G, H 四点共面.
即
?
合作探究
O
A
B
C
D
E
F
G
H
∴ E, F, G, H 四点共面.
∴ E, F, G, H 四点共面.
思考:比较两个解题过程,有没有新的发现?
还可以变为
空间中,同起点出发的四个向量
合作探究
O
A
B
C
D
E
F
G
H
空间中,同起点出发的四个向量
联想:平面向量中有没有类似的结论?
A, B, C 三点共线的充要条件是:
O
A
B
C
空间向量也适用这个结论
数学建构
(2) A, B, C 三点共线的充要条件是:
(4) A、B、C、D 四点共面的充要条件是:
数学应用
例2.如图:PA⊥平面ABCD,ABCD是矩形,M、N分别是AB、PC中点。 求证:MN//平面PAD
B
C
A
D
P
M
N
E
F
课堂小结
(2) A, B, C 三点共线的充要条件是:
(4) A、B、C、D 四点共面的充要条件是:
巩固提升
1.下列命题中正确的有:
A.1个 B.2个 C.3个 D.4个
2.下列说法正确的是:
A.平面内的任意两个向量都共线
B.空间的任意三个向量都不共面
C.空间的任意两个向量都共面
D.空间的任意三个向量都共面
√
√
√
√
巩固提升
3.对于空间中的三个向量 它们一定是:
A.共面向量 B.共线向量
C.不共面向量 D.既不共线又不共面向量
4.已知点M在平面ABC内,并且对空间任意一点O, ,则x的值为:
√
√
巩固提升
5、已知A、B、C三点不共线,就平面ABC外任一点O,确定在下列各条件下,点M是否与A、B、C一定共面:
√
√
复习引入
问题1:空间任意两向量是共线向量吗?你来谈一谈
图:
式:
可以平移到一条直线上
问题2:空间任意两向量是共面吗?你来谈一谈
空间任意两个向量都可以平移到同一个平面内,成为同一平面内的两个向量.
合作探究
问题3:空间中三个不共线的非零向量共面吗?你来谈一谈
A
B
E
C
F
D
H
G
比如. 在正方体, AC 与 EF 与DH 共面吗
A
B
E
C
F
D
H
G
W
比如. 在正方体, AC 与 EW 与DH 共面吗
问题4. 在空间, a 与 b 与c 需要满足什么条件才能共面呢?
合作探究
问题4. 在空间, a 与 b 与c 需要满足什么条件才能共面呢?
平面内,如果两个向量 a, b 不共线, 那么向量 c 与向量 a, b 共面的充要条件是存在惟一的有序实数对 (x, y), 使c=xa+yb.
联想:平面向量的基本定理
空间中,如果两个向量 a, b 不共线, 那么向量 c 与向量 a, b 共面的充要条件是存在惟一的有序实数对 (x, y), 使c=xa+yb.
空间中这个定理还是用吗?
数学建构
空间中,如果两个向量 a, b 不共线, 那么向量 c 与向量 a, b 共面的充要条件是存在惟一的有序实数对 (x, y), 使c=xa+yb.
共面向量定理(即:平面向量基本定理)
数学应用
例1. 如图, 已知平行四边形 ABCD, 过平面 AC外一点 O 作射线 OA, OB, OC, OD, 的四条射线上分别取上 E, F, G, H, 并且使 求证: E, F, G, H 四点共面.
O
A
B
C
D
E
F
G
H
分析:
用 表示
用 表示
用 表示;
用 表示.
用 表示
用 表示
用 表示
而
数学应用
证明:
在平行四边形ABCD中,
得
由已知得
于是得
∴ E, F, G, H 四点共面.
O
A
B
C
D
E
F
G
H
例1. 如图, 已知平行四边形 ABCD, 过平面 AC外一点 O 作射线 OA, OB, OC, OD, 的四条射线上分别取上 E, F, G, H, 并且使 求证: E, F, G, H 四点共面.
还有其他思路吗?
∴ E, F, G, H 四点共面.
?
?
数学应用
O
A
B
C
D
E
F
G
H
变. 如图, 已知平行四边形 ABCD, 过平面 AC外一点 O 作射线 OA, OB, OC, OD, 的四条射线上分别取上 E, F, G, H, 并且使 求证: E, F, G, H 四点共面.
证明:
在平行四边形ABCD中,
得
由已知得
∴ E, F, G, H 四点共面.
即
?
合作探究
O
A
B
C
D
E
F
G
H
∴ E, F, G, H 四点共面.
∴ E, F, G, H 四点共面.
思考:比较两个解题过程,有没有新的发现?
还可以变为
空间中,同起点出发的四个向量
合作探究
O
A
B
C
D
E
F
G
H
空间中,同起点出发的四个向量
联想:平面向量中有没有类似的结论?
A, B, C 三点共线的充要条件是:
O
A
B
C
空间向量也适用这个结论
数学建构
(2) A, B, C 三点共线的充要条件是:
(4) A、B、C、D 四点共面的充要条件是:
数学应用
例2.如图:PA⊥平面ABCD,ABCD是矩形,M、N分别是AB、PC中点。 求证:MN//平面PAD
B
C
A
D
P
M
N
E
F
课堂小结
(2) A, B, C 三点共线的充要条件是:
(4) A、B、C、D 四点共面的充要条件是:
巩固提升
1.下列命题中正确的有:
A.1个 B.2个 C.3个 D.4个
2.下列说法正确的是:
A.平面内的任意两个向量都共线
B.空间的任意三个向量都不共面
C.空间的任意两个向量都共面
D.空间的任意三个向量都共面
√
√
√
√
巩固提升
3.对于空间中的三个向量 它们一定是:
A.共面向量 B.共线向量
C.不共面向量 D.既不共线又不共面向量
4.已知点M在平面ABC内,并且对空间任意一点O, ,则x的值为:
√
√
巩固提升
5、已知A、B、C三点不共线,就平面ABC外任一点O,确定在下列各条件下,点M是否与A、B、C一定共面:
√
√
