苏教版(2019)高中数学选择性必修第二册 6.3.3空间角的计算 课件(共16张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第二册 6.3.3空间角的计算 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 627.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 09:27:30 | ||
图片预览


文档简介
(共16张PPT)
6.3.3空间角的计算
学习目标
1.理解向量成角与线线角、线面角、面面角之间的关系;
2.能用向量方法解决线线、线面的夹角的计算问题;
3.核心素养:直观想象、数学运算;
4.活动体验:感受利用类比、归纳方法的探究过程。
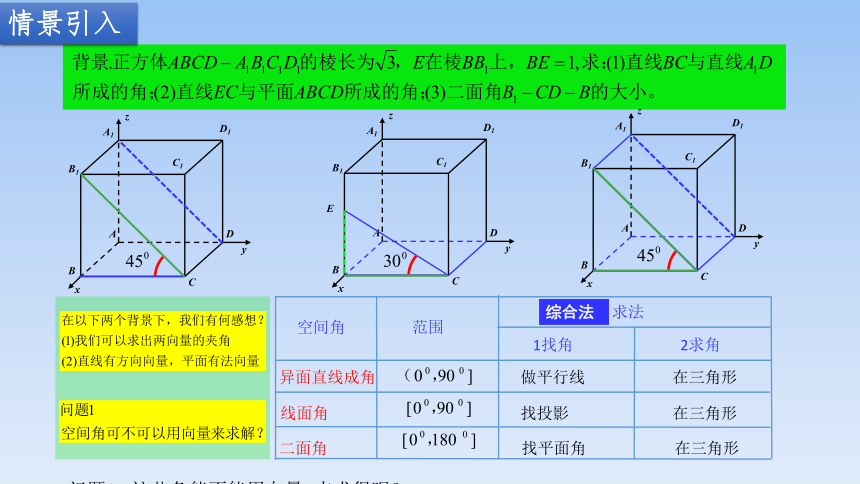
情景引入
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
异面直线成角
线面角
二面角
做平行线
找投影
找平面角
在三角形
在三角形
在三角形
1找角
2求角
空间角
范围
求法
E
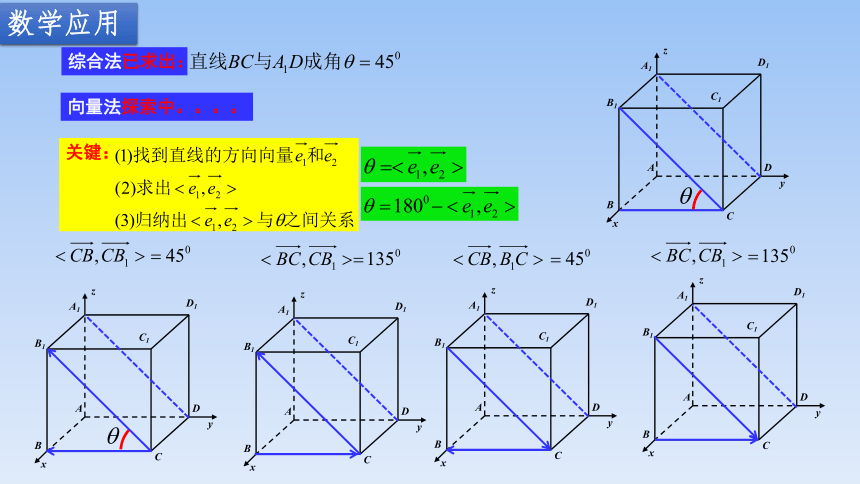
综合法
数学应用
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
综合法已求出:
向量法探索中。。。。
关键:
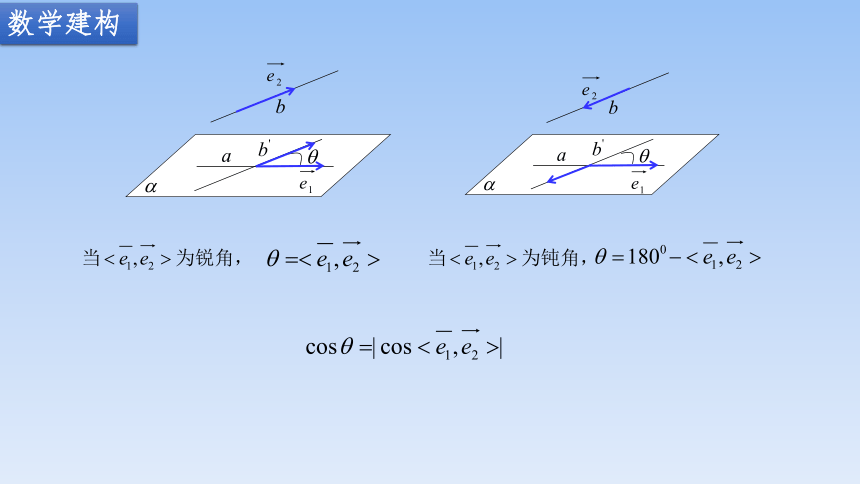
数学建构
数学应用
A
A1
B1
C1
D1
D
C
B
z
y
x
E
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
E
E
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
E
E
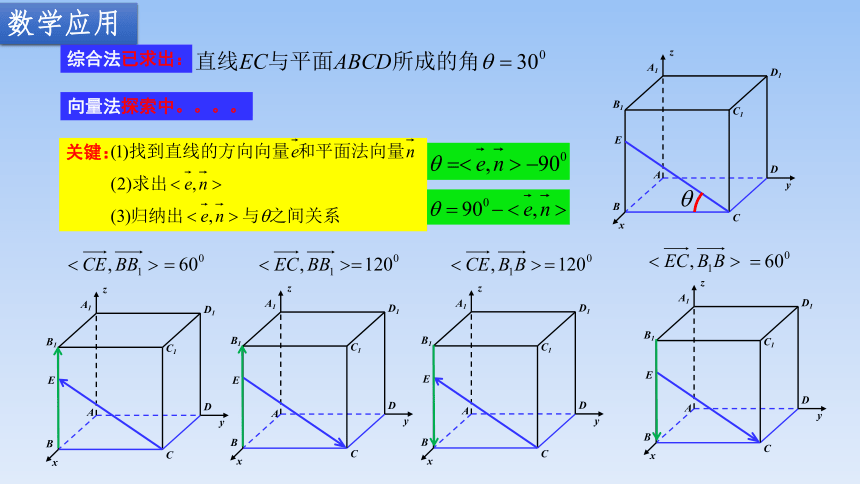
综合法已求出:
向量法探索中。。。。
关键:
数学应用
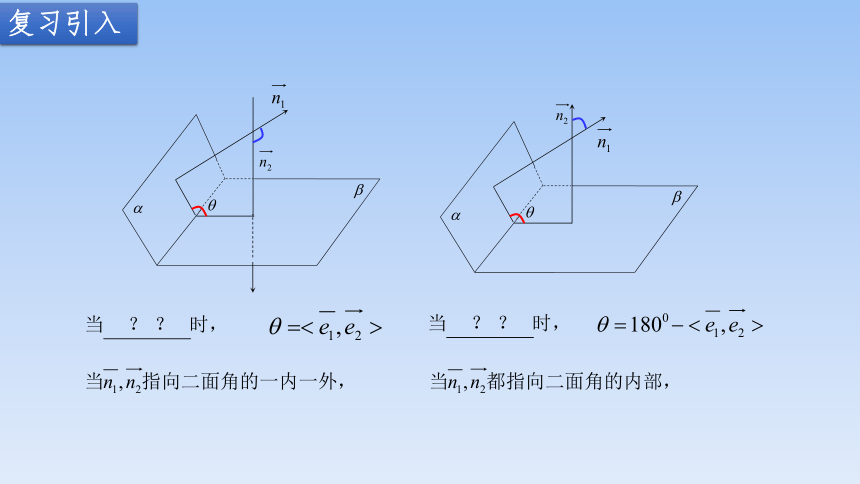
复习引入
数学应用
D1
B1
D
B
C
C1
y
E1
F1
H
G
A1
x
A
z
数学应用
A1
D1
B1
A
D
B
C
C1
y
E1
F
x
z
数学应用
数学应用
课堂小结
空间角
找角
不找角
在三角形角中求
用向量求
用向量求
综合法
向量法
课堂达标
课堂达标
2. 已知△ABC和△DBC所在的平面互相垂直, 且AB=BC=BD, ∠CBA=∠DBC=120 , 求:
(1) 直线AD与平面BCD所成角的大小;(2) 直线AD与直线BC所成角的大小;
(3) 二面角A-BD-C的余弦值.
A
B
C
D
解:
∵平面ABC⊥平面DBC,
∴ 作AO⊥BC, 垂足为O,
则 AO⊥平面DBC.
O
连结DO,
由△ABO≌△DBO 得 AO=DO,
则∠ADO为
(1)
AD与平面BCD所成的角.
∴∠ADO=45 ,
即直线AD与平面BCD所成的角是45 .
由△ABO≌△DBO 得 ∠DOB=90 ,
(2)
∴BC⊥平面AOD,
得 BC⊥AD,
∴直线AD与直线BC所成的角为90 .
课堂达标
2. 已知△ABC和△DBC所在的平面互相垂直, 且AB=BC=BD, ∠CBA=∠DBC=120 , 求:
(1) 直线AD与平面BCD所成角的大小;(2) 直线AD与直线BC所成角的大小;
(3) 二面角A-BD-C的余弦值.
A
B
C
D
解:
∵平面ABC⊥平面DBC,
∴ 作AO⊥BC, 垂足为O,
则 AO⊥平面DBC.
O
x
y
(3)
分别以OD, OC, OA为 x轴,
设 AB=BC=BD=
则 A(0, 0, 3),
D(3, 0, 0),
y轴, z轴建立空间直角坐标系,
平面BDC的法向量平行于OA, 设为 u=(0, 0, 1).
设平面ABD的法向量为 v=(x, y, z),
z
课堂达标
2. 已知△ABC和△DBC所在的平面互相垂直, 且AB=BC=BD, ∠CBA=∠DBC=120 , 求:
(1) 直线AD与平面BCD所成角的大小;(2) 直线AD与直线BC所成角的大小;
(3) 二面角A-BD-C的余弦值.
A
B
C
D
O
x
y
z
由 得
由 得
取 x=1, z=1,
即得
则
因为二面角A-BD-C的大小与两平面法向量的夹角互补,
所以二面角A-BD-C的余弦值为
6.3.3空间角的计算
学习目标
1.理解向量成角与线线角、线面角、面面角之间的关系;
2.能用向量方法解决线线、线面的夹角的计算问题;
3.核心素养:直观想象、数学运算;
4.活动体验:感受利用类比、归纳方法的探究过程。
情景引入
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
异面直线成角
线面角
二面角
做平行线
找投影
找平面角
在三角形
在三角形
在三角形
1找角
2求角
空间角
范围
求法
E
综合法
数学应用
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
综合法已求出:
向量法探索中。。。。
关键:
数学建构
数学应用
A
A1
B1
C1
D1
D
C
B
z
y
x
E
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
E
E
A
A1
B1
C1
D1
D
C
B
z
y
x
A
A1
B1
C1
D1
D
C
B
z
y
x
E
E
综合法已求出:
向量法探索中。。。。
关键:
数学应用
复习引入
数学应用
D1
B1
D
B
C
C1
y
E1
F1
H
G
A1
x
A
z
数学应用
A1
D1
B1
A
D
B
C
C1
y
E1
F
x
z
数学应用
数学应用
课堂小结
空间角
找角
不找角
在三角形角中求
用向量求
用向量求
综合法
向量法
课堂达标
课堂达标
2. 已知△ABC和△DBC所在的平面互相垂直, 且AB=BC=BD, ∠CBA=∠DBC=120 , 求:
(1) 直线AD与平面BCD所成角的大小;(2) 直线AD与直线BC所成角的大小;
(3) 二面角A-BD-C的余弦值.
A
B
C
D
解:
∵平面ABC⊥平面DBC,
∴ 作AO⊥BC, 垂足为O,
则 AO⊥平面DBC.
O
连结DO,
由△ABO≌△DBO 得 AO=DO,
则∠ADO为
(1)
AD与平面BCD所成的角.
∴∠ADO=45 ,
即直线AD与平面BCD所成的角是45 .
由△ABO≌△DBO 得 ∠DOB=90 ,
(2)
∴BC⊥平面AOD,
得 BC⊥AD,
∴直线AD与直线BC所成的角为90 .
课堂达标
2. 已知△ABC和△DBC所在的平面互相垂直, 且AB=BC=BD, ∠CBA=∠DBC=120 , 求:
(1) 直线AD与平面BCD所成角的大小;(2) 直线AD与直线BC所成角的大小;
(3) 二面角A-BD-C的余弦值.
A
B
C
D
解:
∵平面ABC⊥平面DBC,
∴ 作AO⊥BC, 垂足为O,
则 AO⊥平面DBC.
O
x
y
(3)
分别以OD, OC, OA为 x轴,
设 AB=BC=BD=
则 A(0, 0, 3),
D(3, 0, 0),
y轴, z轴建立空间直角坐标系,
平面BDC的法向量平行于OA, 设为 u=(0, 0, 1).
设平面ABD的法向量为 v=(x, y, z),
z
课堂达标
2. 已知△ABC和△DBC所在的平面互相垂直, 且AB=BC=BD, ∠CBA=∠DBC=120 , 求:
(1) 直线AD与平面BCD所成角的大小;(2) 直线AD与直线BC所成角的大小;
(3) 二面角A-BD-C的余弦值.
A
B
C
D
O
x
y
z
由 得
由 得
取 x=1, z=1,
即得
则
因为二面角A-BD-C的大小与两平面法向量的夹角互补,
所以二面角A-BD-C的余弦值为
