苏教版(2019)高中数学选择性必修第二册 7.1 两个基本计数原理课件(共15张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第二册 7.1 两个基本计数原理课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 586.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 10:18:57 | ||
图片预览






文档简介
(共15张PPT)
7.1两个基本计数原理
学习目标
1.理解分类计数与分步计数原理;
2.能利用分类计数与分步计数原理解决一些简单的计数问题;
3.让学生体会从分类到分步的转变,辨别分类与分步的联系,感受计数原理的生成过程。
情景创设
工学三部学生会换届选举,中午订餐需要参会人员数,你来数一数?
一个一个数-----穷举法
两个两个数-----2×11=22
五个五个数-----5×4+2=22
总结:数数是有方法的
方法一、穷举法
还有没有其他方法?
情景创设
算法一:先分别数出红、黄、绿、蓝的个数,然后相加
算法二:先算出每一捆的个数,及捆数,然后相乘
分别数出左右两张图中的彩棒的个数,并思考算法的步骤
活动探究
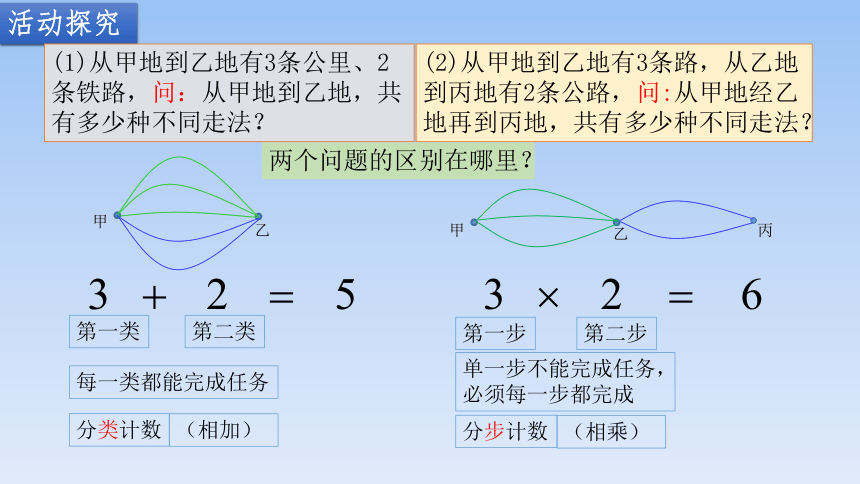
(1)从甲地到乙地有3条公里、2条铁路,问:从甲地到乙地,共有多少种不同走法?
(2)从甲地到乙地有3条路,从乙地到丙地有2条公路,问:从甲地经乙地再到丙地,共有多少种不同走法?
甲
乙
甲
乙
丙
两个问题的区别在哪里?
第一类
第二类
第一步
第二步
每一类都能完成任务
单一步不能完成任务,
必须每一步都完成
分类计数
分步计数
(相加)
(相乘)
数学建构
分类计数原理.
如果完成一件事有n 类不同方案,
在第 1类方案中有 m1 种不同的方法,
在第 2 类方案中有 m2种不同的方法,
在第 3 类方案中有 m3 种不同的方法,
... ... ... ... ,
在第 n类方案中有 mn 种不同的方法.
完成这件事不同的方法种数为:
N=m1+m2+…+mn
分步计数原理.
如果完成一件事需要三个步骤,
做第 1 步有 m1 种不同的方法,
做第 2 步有 m2 种不同的方法,
做第 3 步有 m3 种不同的方法,
... ... ... ... ,
做第 n 步有 mn 种不同的方法.
完成这件事不同的方法种数为:
N=m1×m2×…×mn
数学应用
例1. 书架的第 1 层放有 4 本不同的计算机书, 第 2 层放有 3 本不同的文艺书, 第 3 层放有 2本不同的体育书.
(1) 从书架上任取 1本书, 有多少种不同的取法
(2) 从书架的第 1、2、3 层各取 1 本书, 有多少种不同的取法
解: (1)
第一类:从第1层有 种取法,
第二类:从第2层有 种取法,
第三类:从第 3层有 种取法.
4
3
2
不同的取法种数是
N=4+3+2
=9.
答: 从书架上任取 1本书, 共有 9 种不同的取法.
解: (2)
第一步:从第 1 层有 种取法,
第二步:从第 2 层有 种取法,
第三步:从第 3 层有 种取法.
4
3
2
不同的取法种数是
N=4 3 2
=24.
答:从书架的第 1、2、3 层各取 1 本书,共有 24种不同的取法.
数学应用
例2. 要从甲、乙、丙 3 幅不同的画中选出 2 幅, 分别挂在左、右两边墙上的指定位置, 共有多少种不同的挂法
思路:
先挂一边墙, 再挂另一边墙.
解:
分两步完成这件事:
第 1 步:
在 3 幅画中选 1 幅挂在
左边墙上, 有3 种选法;
第 2 步:
在剩下的 2 幅画中选 1 幅
挂在右边墙上,有 2 种选法.
这是分步计数问题,根据分步乘法计
数原理,不同的挂法种数有
N=3 2=6.
(还有没有其他做法?)
左墙
右墙
甲
乙
甲
丙
乙
乙
甲
丙
丙
丙
甲
乙
左墙
右墙
甲
乙
丙
乙
甲
丙
丙
甲
乙
分类分步计数原理
穷举法
树形图
数学建构
计数
穷 举 法
分类计数
分步计数
树 形 图
分 类
分 步
数学应用
甲地
乙地
丙地
丁地
例3. 如图, 从甲地到乙地有 2 条路, 从乙地到丁地有 3 条路; 从甲地到丙地有 4 条路, 从丙地到丁地有 2 条路. 从甲地到丁地共有多少种不同的路线
解:
从甲地到丁地, 分两类完成事件,
第一类, 从甲经乙到丁,
第一类共有 2 3=6 种路线.
第二类, 从甲经丙到丁,
第二类共有 4 2=8 种路线.
∴ 不同的路线种数共有
N=6+8=14.
(答略)
也分两步:
第一步有 4 条路线, 第二步有 2 条路线,
又分两步,
第一步有 2 条路线,第二步有 3 条路线,
课堂小结
计数原理的应用
1、分清是分类还是分步问题
(1)采用不同的方案都可完成事件属分类;
(2)要分几步才能完成事件, 则每运作一次只是一步.
2、有时分类中含有分步, 分步中也需分类.
数学应用
练. 如图, 一条电路从 A 处到 B 处接通时, 可有多少条不同的线路
○
○
○
○
○
○
○
○
A
B
解:
分三类接通线路 (如图),
一类
二类
三类
第一类, 有 3 种方法;
第二类, 有 1 种方法;
第三类, 分为两步,
每一步都有两种方法,
则第三类有 2 2=4 种方法,
∴共有线路为
N=3+1+4
=8,
答: 共有 8 条不同的线路.
数学建构
计数
穷 举 法
分类计数
分步计数
树 形 图
分 类
分 步
之间 联系?
既能用分类计数(加法)原理,也能用分步计数(乘法)原理
分类 变 分步
每一类的方法个数相同时
课堂达标
1.一件工作可以用 2 种方法完成, 有 5 人只会用第 1 种方法完成, 另有 4 人只会用第 2 种方法完成, 从中选出 1 人来完成这件工作, 不同选法的种数是 ;
解:
从5人或4人中任选 1 人都能完成这件工作,
属分类问题,
第一类, 从5人中选 1 人, 有5种方法;
第二类, 从4人中选 1 人,
N=5+4
= 9.
9
(1)
所以不同选法种数为
有4种方法.
2. 用 1, 5, 9, 13 中任意一个数作分子, 4, 8, 12, 16 中任意一个数作分母, 可构造多少个不同的分数
解:
N=4 4=16.
所以可构成分数个数为
第一步, 构造分子,
有 4 种方法;
第二步,构造分母,
有 4 种方法.
课堂达标
3. 某商场有 6 个门, 如果某人从其中的任意一个门进入商场, 并且要求从其他的门出去, 共有多少种不同的进出商场的方式
解:
进出商场分两步:
第一步, 选择哪道门进去, 有 6 种选法;
第二步, 选择哪道门出来,
先进入那道门不能
选了, 只有 5 种选法.
根据分步乘法原理有
N=6 5=30.
答: 共有30种不同的进出商场方式.
数学建构
4、 4 名同学分别报名参加学校的足球队、篮球队、乒乓球队, 每人限报其中的 1 个运动队, 不同报法的种数是 34 还是 43
5、3 个班分别从 5 个风景点中选择 1 处游览, 不同选法的种数是 35 还是 53
解:
(1)
一个同学一个同学地报名, 报完为止,分为 4 步.
第一个同学报名, 有 3 种报法;
同理, 第二个、第三个、第四个同学逐一去报名,
都有 3 种报法.
∴ 报名方法种数应为 3 3 3 3
=34.
解:
(2)
一个班一个班地逐一选景点, 三个班都选好为止,分 3 步进行.
每一个班的选法都有 5 种,
∴ 不同选法的种数为 5 5 5
= 53.
7.1两个基本计数原理
学习目标
1.理解分类计数与分步计数原理;
2.能利用分类计数与分步计数原理解决一些简单的计数问题;
3.让学生体会从分类到分步的转变,辨别分类与分步的联系,感受计数原理的生成过程。
情景创设
工学三部学生会换届选举,中午订餐需要参会人员数,你来数一数?
一个一个数-----穷举法
两个两个数-----2×11=22
五个五个数-----5×4+2=22
总结:数数是有方法的
方法一、穷举法
还有没有其他方法?
情景创设
算法一:先分别数出红、黄、绿、蓝的个数,然后相加
算法二:先算出每一捆的个数,及捆数,然后相乘
分别数出左右两张图中的彩棒的个数,并思考算法的步骤
活动探究
(1)从甲地到乙地有3条公里、2条铁路,问:从甲地到乙地,共有多少种不同走法?
(2)从甲地到乙地有3条路,从乙地到丙地有2条公路,问:从甲地经乙地再到丙地,共有多少种不同走法?
甲
乙
甲
乙
丙
两个问题的区别在哪里?
第一类
第二类
第一步
第二步
每一类都能完成任务
单一步不能完成任务,
必须每一步都完成
分类计数
分步计数
(相加)
(相乘)
数学建构
分类计数原理.
如果完成一件事有n 类不同方案,
在第 1类方案中有 m1 种不同的方法,
在第 2 类方案中有 m2种不同的方法,
在第 3 类方案中有 m3 种不同的方法,
... ... ... ... ,
在第 n类方案中有 mn 种不同的方法.
完成这件事不同的方法种数为:
N=m1+m2+…+mn
分步计数原理.
如果完成一件事需要三个步骤,
做第 1 步有 m1 种不同的方法,
做第 2 步有 m2 种不同的方法,
做第 3 步有 m3 种不同的方法,
... ... ... ... ,
做第 n 步有 mn 种不同的方法.
完成这件事不同的方法种数为:
N=m1×m2×…×mn
数学应用
例1. 书架的第 1 层放有 4 本不同的计算机书, 第 2 层放有 3 本不同的文艺书, 第 3 层放有 2本不同的体育书.
(1) 从书架上任取 1本书, 有多少种不同的取法
(2) 从书架的第 1、2、3 层各取 1 本书, 有多少种不同的取法
解: (1)
第一类:从第1层有 种取法,
第二类:从第2层有 种取法,
第三类:从第 3层有 种取法.
4
3
2
不同的取法种数是
N=4+3+2
=9.
答: 从书架上任取 1本书, 共有 9 种不同的取法.
解: (2)
第一步:从第 1 层有 种取法,
第二步:从第 2 层有 种取法,
第三步:从第 3 层有 种取法.
4
3
2
不同的取法种数是
N=4 3 2
=24.
答:从书架的第 1、2、3 层各取 1 本书,共有 24种不同的取法.
数学应用
例2. 要从甲、乙、丙 3 幅不同的画中选出 2 幅, 分别挂在左、右两边墙上的指定位置, 共有多少种不同的挂法
思路:
先挂一边墙, 再挂另一边墙.
解:
分两步完成这件事:
第 1 步:
在 3 幅画中选 1 幅挂在
左边墙上, 有3 种选法;
第 2 步:
在剩下的 2 幅画中选 1 幅
挂在右边墙上,有 2 种选法.
这是分步计数问题,根据分步乘法计
数原理,不同的挂法种数有
N=3 2=6.
(还有没有其他做法?)
左墙
右墙
甲
乙
甲
丙
乙
乙
甲
丙
丙
丙
甲
乙
左墙
右墙
甲
乙
丙
乙
甲
丙
丙
甲
乙
分类分步计数原理
穷举法
树形图
数学建构
计数
穷 举 法
分类计数
分步计数
树 形 图
分 类
分 步
数学应用
甲地
乙地
丙地
丁地
例3. 如图, 从甲地到乙地有 2 条路, 从乙地到丁地有 3 条路; 从甲地到丙地有 4 条路, 从丙地到丁地有 2 条路. 从甲地到丁地共有多少种不同的路线
解:
从甲地到丁地, 分两类完成事件,
第一类, 从甲经乙到丁,
第一类共有 2 3=6 种路线.
第二类, 从甲经丙到丁,
第二类共有 4 2=8 种路线.
∴ 不同的路线种数共有
N=6+8=14.
(答略)
也分两步:
第一步有 4 条路线, 第二步有 2 条路线,
又分两步,
第一步有 2 条路线,第二步有 3 条路线,
课堂小结
计数原理的应用
1、分清是分类还是分步问题
(1)采用不同的方案都可完成事件属分类;
(2)要分几步才能完成事件, 则每运作一次只是一步.
2、有时分类中含有分步, 分步中也需分类.
数学应用
练. 如图, 一条电路从 A 处到 B 处接通时, 可有多少条不同的线路
○
○
○
○
○
○
○
○
A
B
解:
分三类接通线路 (如图),
一类
二类
三类
第一类, 有 3 种方法;
第二类, 有 1 种方法;
第三类, 分为两步,
每一步都有两种方法,
则第三类有 2 2=4 种方法,
∴共有线路为
N=3+1+4
=8,
答: 共有 8 条不同的线路.
数学建构
计数
穷 举 法
分类计数
分步计数
树 形 图
分 类
分 步
之间 联系?
既能用分类计数(加法)原理,也能用分步计数(乘法)原理
分类 变 分步
每一类的方法个数相同时
课堂达标
1.一件工作可以用 2 种方法完成, 有 5 人只会用第 1 种方法完成, 另有 4 人只会用第 2 种方法完成, 从中选出 1 人来完成这件工作, 不同选法的种数是 ;
解:
从5人或4人中任选 1 人都能完成这件工作,
属分类问题,
第一类, 从5人中选 1 人, 有5种方法;
第二类, 从4人中选 1 人,
N=5+4
= 9.
9
(1)
所以不同选法种数为
有4种方法.
2. 用 1, 5, 9, 13 中任意一个数作分子, 4, 8, 12, 16 中任意一个数作分母, 可构造多少个不同的分数
解:
N=4 4=16.
所以可构成分数个数为
第一步, 构造分子,
有 4 种方法;
第二步,构造分母,
有 4 种方法.
课堂达标
3. 某商场有 6 个门, 如果某人从其中的任意一个门进入商场, 并且要求从其他的门出去, 共有多少种不同的进出商场的方式
解:
进出商场分两步:
第一步, 选择哪道门进去, 有 6 种选法;
第二步, 选择哪道门出来,
先进入那道门不能
选了, 只有 5 种选法.
根据分步乘法原理有
N=6 5=30.
答: 共有30种不同的进出商场方式.
数学建构
4、 4 名同学分别报名参加学校的足球队、篮球队、乒乓球队, 每人限报其中的 1 个运动队, 不同报法的种数是 34 还是 43
5、3 个班分别从 5 个风景点中选择 1 处游览, 不同选法的种数是 35 还是 53
解:
(1)
一个同学一个同学地报名, 报完为止,分为 4 步.
第一个同学报名, 有 3 种报法;
同理, 第二个、第三个、第四个同学逐一去报名,
都有 3 种报法.
∴ 报名方法种数应为 3 3 3 3
=34.
解:
(2)
一个班一个班地逐一选景点, 三个班都选好为止,分 3 步进行.
每一个班的选法都有 5 种,
∴ 不同选法的种数为 5 5 5
= 53.
