§1.3.1函数的最大(小)值[上学期]
文档属性
| 名称 | §1.3.1函数的最大(小)值[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-24 00:00:00 | ||
图片预览




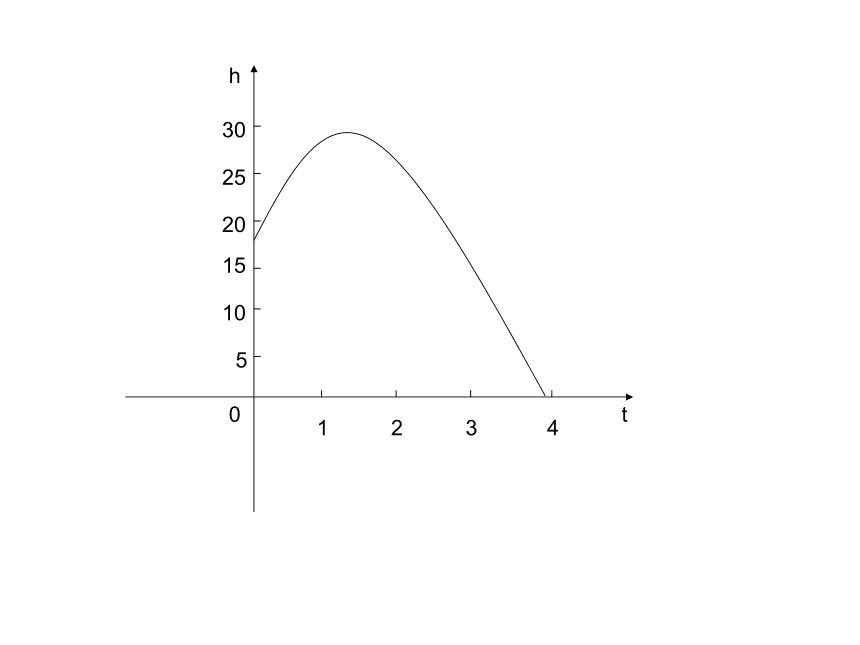
文档简介
课件10张PPT。§1.3.1函数的单调性和最大(小)值
函数的最大(小)值函数的最大值一般地,设函数y=f(x)的定义域为I,如果存在
实数M满足:
(1)对于任意的 ,都有 ;
(2)存在 ,使得
那么,我们称M是函数y=f(x)的最大值
(maximum value)。你能给出函数最小值的定义吗?注意:
1 函数最大(小)首先应该是某一个函数值,它是值域内的一个元素,即存在x0∈I,使得f(x0) = M;
2 函数最大(小)应该是所有函数值中最大(小)的,即对于任意的x∈I,都有f(x)≤M(f(x)≥M).3 对于每个确定函数的最大(小)值不一定存在,如存在一定是唯一的,而其对应的自变量不一定唯一.例 3 “菊花”烟花是最壮观 的烟
花之一。制造时一般是期望在它
达到最高点时爆裂,
如果烟花 距地面的
高度h m与时间t s之间的关系为
h(t)=-4.9t2+14.7t+18 ,那么烟花冲出后什么时候是
它爆裂的最佳时刻?这时距地面的高度是多少? (精确到1m)
例4:已知函数 求函数的
最大值和最小值.分析:由函数 的图象可知,函数
在区间[2,6]上递减.所以,函数在区间[2,6]的
两个端点上分别取得最大值和最小值。 求函数的最大(小)值的方法
1 利用二次函数的性质(配方法)求函数的最大(小)值
2 利用图象求函数的最大(小)值
3 利用函数单调性的求函数的最大(小)值 如果函数y=f(x)在区间[a,b]上单调递增,在区间[b,c]上单调递减,则函数y=f(x)在x=b处有最大值f(b);
如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数b处有最小值f(b);
课堂小结:(1)函数的最大(小)值的概念
(2)求函数的最大(小)值一般方法课后作业: P43 A组T5、B组T2 ①对于熟悉的 一次函数、二次函数、反比例函数等函数可以先画出其图象,根据函数的性质来求最大(小)值 ②对于不熟悉的函数或者比较复杂的函数可以先画 出其图象,观察出其单调性,再用定义证明,然后利用单调性求出函数的最值练习: 分别在下列各范围上求函数
y=x2+2x-3的最值(1) R(2) 1≤x≤2(3) -2≤x≤2图象上有一个最低点(0,0),即对于任意的 ,
都有
图象没有最低点。yx
实数M满足:
(1)对于任意的 ,都有 ;
(2)存在 ,使得
那么,我们称M是函数y=f(x)的最大值
(maximum value)。你能给出函数最小值的定义吗?注意:
1 函数最大(小)首先应该是某一个函数值,它是值域内的一个元素,即存在x0∈I,使得f(x0) = M;
2 函数最大(小)应该是所有函数值中最大(小)的,即对于任意的x∈I,都有f(x)≤M(f(x)≥M).3 对于每个确定函数的最大(小)值不一定存在,如存在一定是唯一的,而其对应的自变量不一定唯一.例 3 “菊花”烟花是最壮观 的烟
花之一。制造时一般是期望在它
达到最高点时爆裂,
如果烟花 距地面的
高度h m与时间t s之间的关系为
h(t)=-4.9t2+14.7t+18 ,那么烟花冲出后什么时候是
它爆裂的最佳时刻?这时距地面的高度是多少? (精确到1m)
例4:已知函数 求函数的
最大值和最小值.分析:由函数 的图象可知,函数
在区间[2,6]上递减.所以,函数在区间[2,6]的
两个端点上分别取得最大值和最小值。 求函数的最大(小)值的方法
1 利用二次函数的性质(配方法)求函数的最大(小)值
2 利用图象求函数的最大(小)值
3 利用函数单调性的求函数的最大(小)值 如果函数y=f(x)在区间[a,b]上单调递增,在区间[b,c]上单调递减,则函数y=f(x)在x=b处有最大值f(b);
如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数b处有最小值f(b);
课堂小结:(1)函数的最大(小)值的概念
(2)求函数的最大(小)值一般方法课后作业: P43 A组T5、B组T2 ①对于熟悉的 一次函数、二次函数、反比例函数等函数可以先画出其图象,根据函数的性质来求最大(小)值 ②对于不熟悉的函数或者比较复杂的函数可以先画 出其图象,观察出其单调性,再用定义证明,然后利用单调性求出函数的最值练习: 分别在下列各范围上求函数
y=x2+2x-3的最值(1) R(2) 1≤x≤2(3) -2≤x≤2图象上有一个最低点(0,0),即对于任意的 ,
都有
图象没有最低点。yx
