苏教版(2019)高中数学选择性必修第二册 7.4.2二项式系数的性质及应用 课件(共16张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第二册 7.4.2二项式系数的性质及应用 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 399.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 13:33:46 | ||
图片预览




文档简介
(共16张PPT)
7.4.2二项式系数的性质及应用
学习目标
1、掌握二项式系数的性质,进一步认识组合数、组合数的性质;
2、会应用二项式系数的性质解决一些简单问题;
3、运用函数观点分析处理二项式系数的性质.
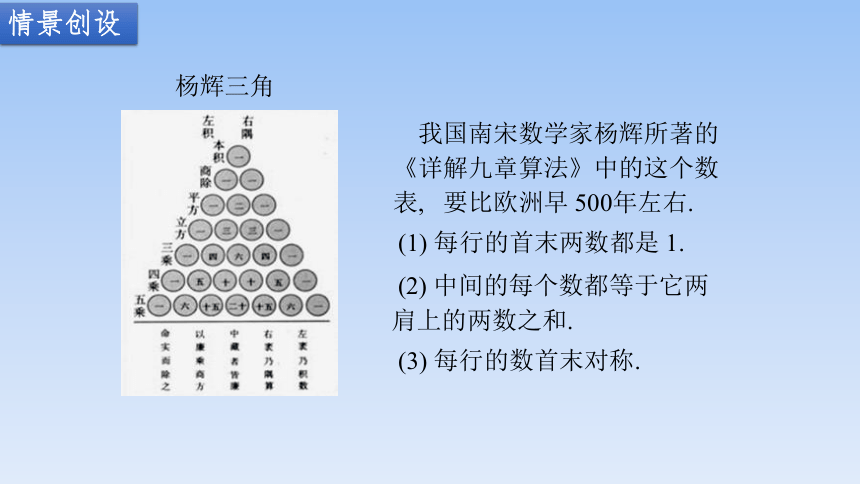
杨辉三角
我国南宋数学家杨辉所著的《详解九章算法》中的这个数表, 要比欧洲早 500年左右.
(1) 每行的首末两数都是 1.
(2) 中间的每个数都等于它两肩上的两数之和.
(3) 每行的数首末对称.
情景创设
情景创设
…………………………………
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
3
4
5
6
6
10
10
15
15
20
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
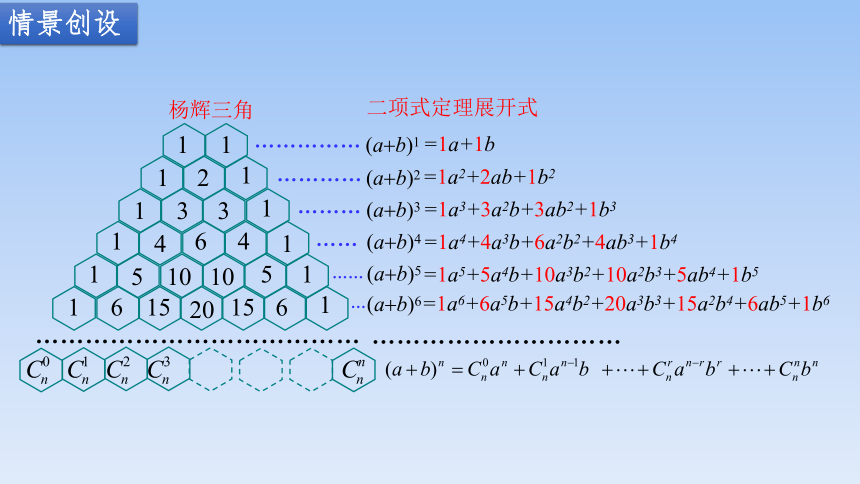
=1a2+2ab+1b2
=1a3+3a2b+3ab2+1b3
=1a4+4a3b+6a2b2+4ab3+1b4
=1a5+5a4b+10a3b2+10a2b3+5ab4+1b5
=1a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+1b6
=1a+1b
…………………………
二项式定理展开式
杨辉三角
情景创设
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
=1a2+2ab+1b2
=1a3+3a2b+3ab2+1b3
=1a4+4a3b+6a2b2+4ab3+1b4
=1a5+5a4b+10a3b2+10a2b3+5ab4+1b5
=1a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+1b6
=1a+1b
…………………………
…………………………………
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
3
4
5
6
6
10
10
15
15
20
二项式定理展开式
杨辉三角
……………
…………
………
……
……
…
归纳探究
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
…………………………………
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
3
4
5
6
6
10
10
15
15
20
杨辉三角
……………
…………
………
……
……
…
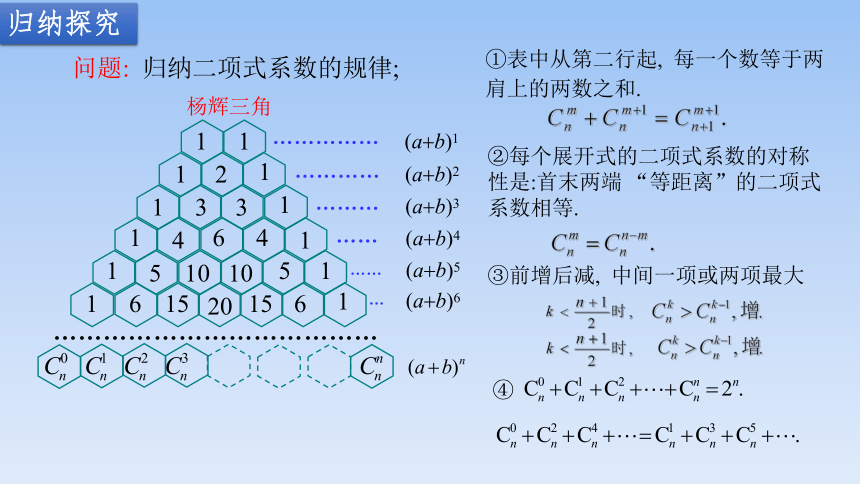
问题: 归纳二项式系数的规律;
①表中从第二行起, 每一个数等于两肩上的两数之和.
②每个展开式的二项式系数的对称性是:首末两端 “等距离”的二项式系数相等.
③前增后减, 中间一项或两项最大
④
数学建构
二项式系数的性质
①表中从第二行起, 每一个数等于两肩上的两数之和.
②每个展开式的二项式系数的对称性是:首末两端 “等距离”的二项式系数相等.
③前增后减, 中间一项或两项最大
④
在组合数中已证明
在组合数中已证明
如何证明
如何证明
在组合数中已证明
数学论证
方法提炼
1、赋值法
数学应用
练. 求证:
证明:
∵ (2-1)n =
而 (2-1)n =1,
数学论证
总结:利用比较法比较大小
数学应用
例3. 求 (1+2x)10 展开式中二项式系数最大的项和系数最大的项.
解:
∵ 二项展开式有 11 项,
中间一项, 即第 6 项的
二项式系数最大,
∴ T6 =
= 8064 x5.
(1) 求二项式系数最大的项:
(2) 求系数最大的项:
设第 k+1 项的系数最大, 则须
解不等式组得
则 k 取整数 7,
∴ 系数最大项为 T8=
= 15360 x7.
数学应用
例4. 已知 (1+x)n 的展开式中第 4 项与第 8 项的二项式系数相等, 求这两项的二项式系数.
解:
由题意得
∴ 3 = n-7,
解得 n=10,
得这两项的二项式系数为
= 120.
情景创设
例5. 用二项式定理证明:(n+1)n-1 能被 n2 整除;
证明:
∵(n+1)n-1
展开式中的每一项都有 n2 的因式,
∴ 原式能被 n2 整除.
课堂小结
二项式系数的性质应用
课堂达标
课堂达标
2. 用二项式定理证明: 9910-1 能被 1000 整除.
证明:
∵9910-1= (100-1)10-1
展开式中的每一项都有1000 的因式,
∴ 原式能被 1000 整除.
7.4.2二项式系数的性质及应用
学习目标
1、掌握二项式系数的性质,进一步认识组合数、组合数的性质;
2、会应用二项式系数的性质解决一些简单问题;
3、运用函数观点分析处理二项式系数的性质.
杨辉三角
我国南宋数学家杨辉所著的《详解九章算法》中的这个数表, 要比欧洲早 500年左右.
(1) 每行的首末两数都是 1.
(2) 中间的每个数都等于它两肩上的两数之和.
(3) 每行的数首末对称.
情景创设
情景创设
…………………………………
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
3
4
5
6
6
10
10
15
15
20
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
=1a2+2ab+1b2
=1a3+3a2b+3ab2+1b3
=1a4+4a3b+6a2b2+4ab3+1b4
=1a5+5a4b+10a3b2+10a2b3+5ab4+1b5
=1a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+1b6
=1a+1b
…………………………
二项式定理展开式
杨辉三角
情景创设
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
=1a2+2ab+1b2
=1a3+3a2b+3ab2+1b3
=1a4+4a3b+6a2b2+4ab3+1b4
=1a5+5a4b+10a3b2+10a2b3+5ab4+1b5
=1a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+1b6
=1a+1b
…………………………
…………………………………
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
3
4
5
6
6
10
10
15
15
20
二项式定理展开式
杨辉三角
……………
…………
………
……
……
…
归纳探究
(a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
…………………………………
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
3
4
5
6
6
10
10
15
15
20
杨辉三角
……………
…………
………
……
……
…
问题: 归纳二项式系数的规律;
①表中从第二行起, 每一个数等于两肩上的两数之和.
②每个展开式的二项式系数的对称性是:首末两端 “等距离”的二项式系数相等.
③前增后减, 中间一项或两项最大
④
数学建构
二项式系数的性质
①表中从第二行起, 每一个数等于两肩上的两数之和.
②每个展开式的二项式系数的对称性是:首末两端 “等距离”的二项式系数相等.
③前增后减, 中间一项或两项最大
④
在组合数中已证明
在组合数中已证明
如何证明
如何证明
在组合数中已证明
数学论证
方法提炼
1、赋值法
数学应用
练. 求证:
证明:
∵ (2-1)n =
而 (2-1)n =1,
数学论证
总结:利用比较法比较大小
数学应用
例3. 求 (1+2x)10 展开式中二项式系数最大的项和系数最大的项.
解:
∵ 二项展开式有 11 项,
中间一项, 即第 6 项的
二项式系数最大,
∴ T6 =
= 8064 x5.
(1) 求二项式系数最大的项:
(2) 求系数最大的项:
设第 k+1 项的系数最大, 则须
解不等式组得
则 k 取整数 7,
∴ 系数最大项为 T8=
= 15360 x7.
数学应用
例4. 已知 (1+x)n 的展开式中第 4 项与第 8 项的二项式系数相等, 求这两项的二项式系数.
解:
由题意得
∴ 3 = n-7,
解得 n=10,
得这两项的二项式系数为
= 120.
情景创设
例5. 用二项式定理证明:(n+1)n-1 能被 n2 整除;
证明:
∵(n+1)n-1
展开式中的每一项都有 n2 的因式,
∴ 原式能被 n2 整除.
课堂小结
二项式系数的性质应用
课堂达标
课堂达标
2. 用二项式定理证明: 9910-1 能被 1000 整除.
证明:
∵9910-1= (100-1)10-1
展开式中的每一项都有1000 的因式,
∴ 原式能被 1000 整除.
