函数的奇偶性[上学期]
图片预览




文档简介
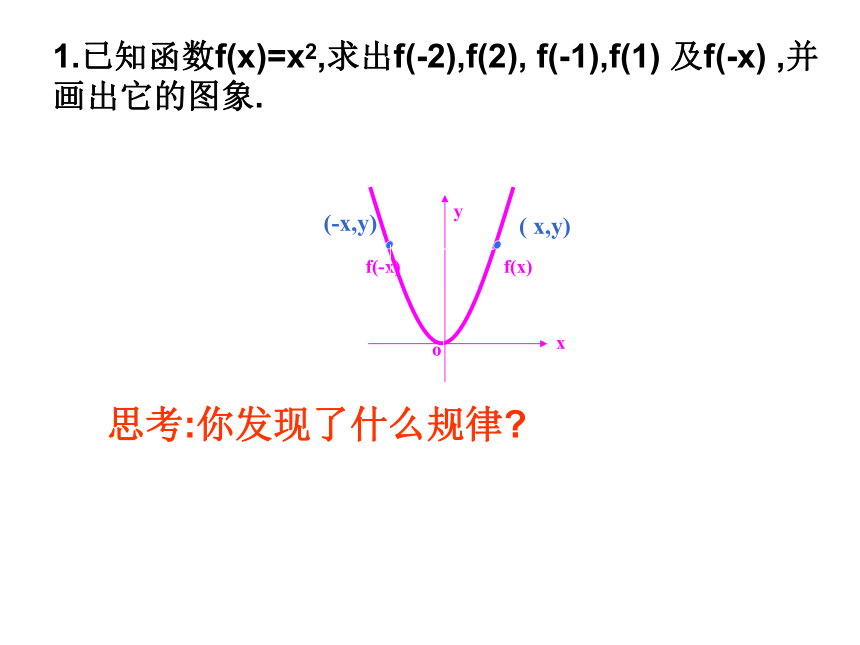
课件17张PPT。o函数的奇偶性 1.已知函数f(x)=x2,求出f(-2),f(2), f(-1),f(1) 及f(-x) ,并
画出它的图象.
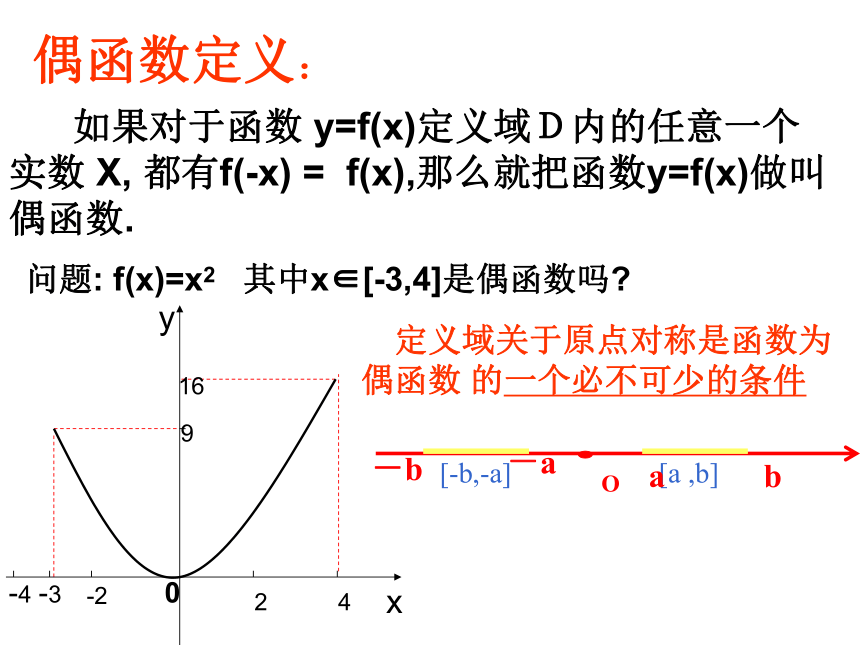
思考:你发现了什么规律?偶函数定义: 如果对于函数 y=f(x)定义域D内的任意一个实数 X, 都有f(-x) = f(x),那么就把函数y=f(x)做叫偶函数.
问题: f(x)=x2 其中x∈[-3,4]是偶函数吗? 定义域关于原点对称是函数为
偶函数 的一个必不可少的条件Oab-a-b例1. 判断下列函数的奇偶性 ⑴先求定义域,看是否关于原点对称;
⑵再判断f(-x)=-f(x)或f(-x)=f(x) 是否成立。☆ 说明:用定义判断函数奇偶性的步骤:问题: 观察这几个偶函数的图象,你能得到偶函数
的图象的共同特征吗?你能得到奇函数的图象的
共同特征吗?
奇、偶函数图象的性质: ⑴ 偶函数的图象关于y轴对称.
(2) 奇函数的图象关于原点对称.
反之,如果一个函数的图象关于原点对称,那么这个函数是奇函数. 反之, 如果一个函数的图象关于 y 轴对称,那 么这个函数是偶函数.解:画法略 y x 023.8-2-3.8例2 已知函数y=f(x)是偶函数,它在 y轴右边的图象如图,根据函数的奇偶性画出它在 y轴左边 的图象 . 注: 奇、偶函数图象的特征可用于:
①.简化函数图象的画法。
②.判断函数的奇偶性。小结
奇函数的图象关于原点对称
偶函数的图象关于
y轴对称小结1、奇函数和偶函数的定义及图象特征?2、判断函数奇偶性的前提条件是什么?
3、判断函数奇偶性的一般步骤是什么?函数的定义域是否
关于原点对称 小结1.函数的定义域是否关于原点对称;
2.是否定义域内的任意实数x都有f(-x)=f(x)或f(-x)=-f(x)成立;1、奇函数和偶函数的定义及图象特征?2、判断函数奇偶性的前提条件是什么?
3、判断函数奇偶性的注意事项小结1.函数的定义域是否关于原点对称;
2.是否定义域内的任意实数x都有f(-x)=f(x)或f(-x)=-f(x)成立;1、奇函数和偶函数的定义及图象特征?2、判断函数奇偶性的前提条件是什么?3、判断函数奇偶性的一般步骤是什么?
课外作业: P43 A组T6 练习1. 判断下列函数的奇偶性说明:根据函数的奇偶性, 函数可划分为四类:
画出它的图象.
思考:你发现了什么规律?偶函数定义: 如果对于函数 y=f(x)定义域D内的任意一个实数 X, 都有f(-x) = f(x),那么就把函数y=f(x)做叫偶函数.
问题: f(x)=x2 其中x∈[-3,4]是偶函数吗? 定义域关于原点对称是函数为
偶函数 的一个必不可少的条件Oab-a-b例1. 判断下列函数的奇偶性 ⑴先求定义域,看是否关于原点对称;
⑵再判断f(-x)=-f(x)或f(-x)=f(x) 是否成立。☆ 说明:用定义判断函数奇偶性的步骤:问题: 观察这几个偶函数的图象,你能得到偶函数
的图象的共同特征吗?你能得到奇函数的图象的
共同特征吗?
奇、偶函数图象的性质: ⑴ 偶函数的图象关于y轴对称.
(2) 奇函数的图象关于原点对称.
反之,如果一个函数的图象关于原点对称,那么这个函数是奇函数. 反之, 如果一个函数的图象关于 y 轴对称,那 么这个函数是偶函数.解:画法略 y x 023.8-2-3.8例2 已知函数y=f(x)是偶函数,它在 y轴右边的图象如图,根据函数的奇偶性画出它在 y轴左边 的图象 . 注: 奇、偶函数图象的特征可用于:
①.简化函数图象的画法。
②.判断函数的奇偶性。小结
奇函数的图象关于原点对称
偶函数的图象关于
y轴对称小结1、奇函数和偶函数的定义及图象特征?2、判断函数奇偶性的前提条件是什么?
3、判断函数奇偶性的一般步骤是什么?函数的定义域是否
关于原点对称 小结1.函数的定义域是否关于原点对称;
2.是否定义域内的任意实数x都有f(-x)=f(x)或f(-x)=-f(x)成立;1、奇函数和偶函数的定义及图象特征?2、判断函数奇偶性的前提条件是什么?
3、判断函数奇偶性的注意事项小结1.函数的定义域是否关于原点对称;
2.是否定义域内的任意实数x都有f(-x)=f(x)或f(-x)=-f(x)成立;1、奇函数和偶函数的定义及图象特征?2、判断函数奇偶性的前提条件是什么?3、判断函数奇偶性的一般步骤是什么?
课外作业: P43 A组T6 练习1. 判断下列函数的奇偶性说明:根据函数的奇偶性, 函数可划分为四类:
