函数的单调性[上学期]
图片预览




文档简介
课件17张PPT。函数的单调性
即墨市第二职业中专
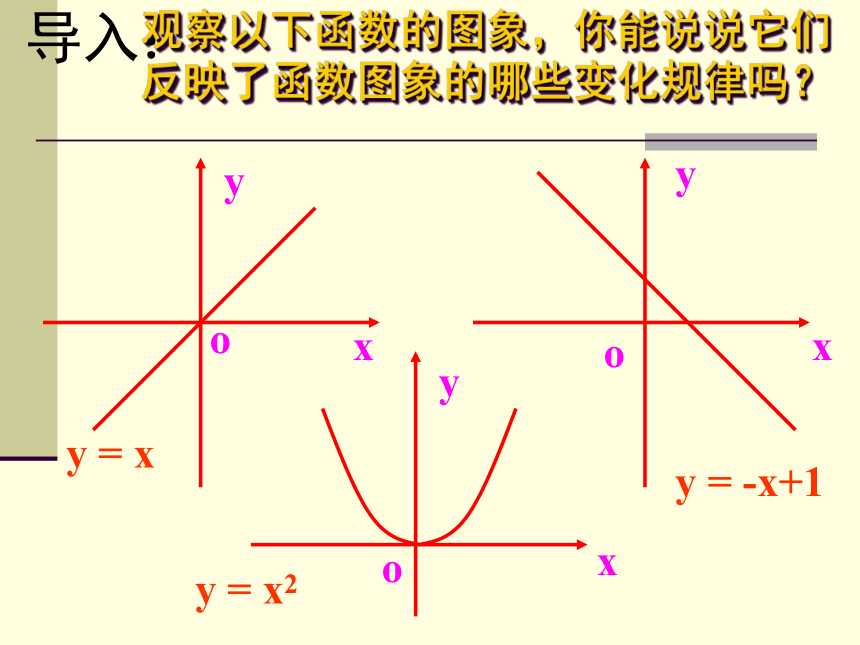
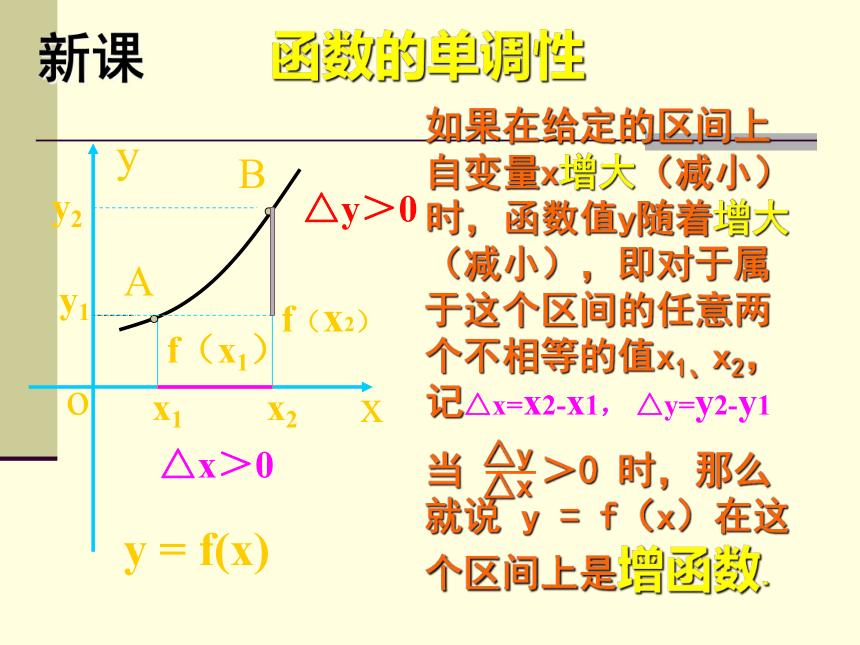
黄小调3.3.1 函数的单调性y = x y = -x+1y = x2x xyyooxyo观察以下函数的图象,你能说说它们反映了函数图象的哪些变化规律吗?导入:函数的单调性△y>0xyoA x1x2Bf(x1)f(x2)y1y2y = f(x)△x>0新课f(x2)yxoABx1x2f(x1)y2y1y = f(x)△y<0△x>0函数的单调性图象特征数学语言从左向右逐渐上升从左向右逐渐下降函数的单调性 函数的单调区间,一般是指保持函数单调性的最大区间.函数的单调性
如果一个函数在某个区间上是增函数或是减函数就说这个函数在这个区间上具有(严格的)单调性例题 例1:如图,函数y=f(x)的定义域是[-10,10],根据图象指出函数y=f(x)的单调区间,并指出在每一个单调区间上函数y=f(x)的单调性。 从图像上,比比我们谁先找到函数的单调区间?解:函数y=f(x)的单调区间有:[-10,-4],(-4,-1],(-1,2],(2,8],(8,10]其中函数y=f(x)在区间[-10,-4], (-1,2] ,(8,10]上是减函数;在区间(-4,-1]
, (2,8]上是增函数。判断函数单调性的一般步骤1、在给定的区间上任取两个不相等的自变量的值x1,x2则从而计算出⊿y2、计算出3、当k>0时,函数y=f(x)在这个区间上是增函数
当k<0时,函数y=f(x)在这个区间上是减函数△x=x2-x1 例2、证明函数f(x)=2x+1在 上是增函数证明:设 是任意两个不相等的实数因为因此函数f(x)=2x+1在 上是增函数。例题思考一下,证明的步骤是???例题证明:设 是任意两个不相等的负实数, 例3、证明函数f(x)= 在 上是减函数因此,函数f(x)= 在区间 上是减函数课堂练习⑶ 证明函数 f(x)= x2 在 (-∞,0)上是减函数. ⑷证明函数f(x)= x2在(0, +∞)上是增函数.练习观察图象,请你根据图象说出函数单调性的定义回顾
1、这节课我们学习了函数单调性的定义,要特别注意定义中“给定区间”、“任意”、“不相等”这几个关键词语;在写单调区间时不要轻易用并集的符号连接;、
2、证明函数的单调性时,应该注意证明的几个步骤。
小结:⑴如果函数y=f(x)是区间(- ∞, +∞)上的增函数,
①求证k>0时, kf(x)在区间(- ∞, +∞)上也是增函数
②k<0时,判断函数kf(x)在区间(- ∞, +∞)上的单调性,并证明之.
⑵思考你对单调性定义中“严格”的理解.思考
祝同学们 学习进步!
即墨市第二职业中专
黄小调3.3.1 函数的单调性y = x y = -x+1y = x2x xyyooxyo观察以下函数的图象,你能说说它们反映了函数图象的哪些变化规律吗?导入:函数的单调性△y>0xyoA x1x2Bf(x1)f(x2)y1y2y = f(x)△x>0新课f(x2)yxoABx1x2f(x1)y2y1y = f(x)△y<0△x>0函数的单调性图象特征数学语言从左向右逐渐上升从左向右逐渐下降函数的单调性 函数的单调区间,一般是指保持函数单调性的最大区间.函数的单调性
如果一个函数在某个区间上是增函数或是减函数就说这个函数在这个区间上具有(严格的)单调性例题 例1:如图,函数y=f(x)的定义域是[-10,10],根据图象指出函数y=f(x)的单调区间,并指出在每一个单调区间上函数y=f(x)的单调性。 从图像上,比比我们谁先找到函数的单调区间?解:函数y=f(x)的单调区间有:[-10,-4],(-4,-1],(-1,2],(2,8],(8,10]其中函数y=f(x)在区间[-10,-4], (-1,2] ,(8,10]上是减函数;在区间(-4,-1]
, (2,8]上是增函数。判断函数单调性的一般步骤1、在给定的区间上任取两个不相等的自变量的值x1,x2则从而计算出⊿y2、计算出3、当k>0时,函数y=f(x)在这个区间上是增函数
当k<0时,函数y=f(x)在这个区间上是减函数△x=x2-x1 例2、证明函数f(x)=2x+1在 上是增函数证明:设 是任意两个不相等的实数因为因此函数f(x)=2x+1在 上是增函数。例题思考一下,证明的步骤是???例题证明:设 是任意两个不相等的负实数, 例3、证明函数f(x)= 在 上是减函数因此,函数f(x)= 在区间 上是减函数课堂练习⑶ 证明函数 f(x)= x2 在 (-∞,0)上是减函数. ⑷证明函数f(x)= x2在(0, +∞)上是增函数.练习观察图象,请你根据图象说出函数单调性的定义回顾
1、这节课我们学习了函数单调性的定义,要特别注意定义中“给定区间”、“任意”、“不相等”这几个关键词语;在写单调区间时不要轻易用并集的符号连接;、
2、证明函数的单调性时,应该注意证明的几个步骤。
小结:⑴如果函数y=f(x)是区间(- ∞, +∞)上的增函数,
①求证k>0时, kf(x)在区间(- ∞, +∞)上也是增函数
②k<0时,判断函数kf(x)在区间(- ∞, +∞)上的单调性,并证明之.
⑵思考你对单调性定义中“严格”的理解.思考
祝同学们 学习进步!
