人教版数学七年级下册5.3.1平行线的性质 课件(共20张PPT)
文档属性
| 名称 | 人教版数学七年级下册5.3.1平行线的性质 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 988.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 11:22:34 | ||
图片预览



文档简介
(共20张PPT)
学习目标:
1、理解并熟记平行线的性质;
2、能够应用平行线的性质进行简单的推理和计算。
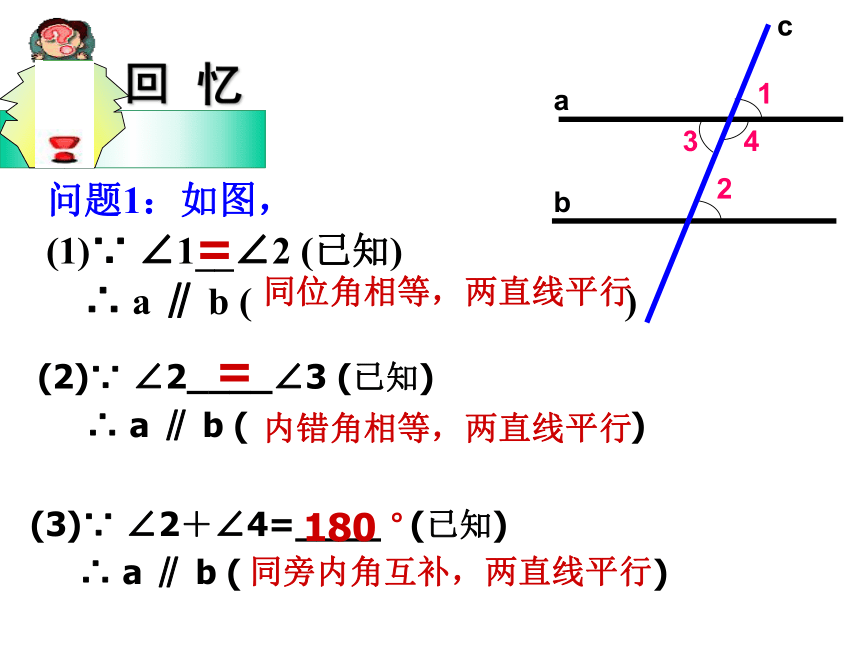
问题1:如图,
(1)∵ ∠1__∠2 (已知)
∴ a ∥ b ( )
(2)∵ ∠2____∠3 (已知)
∴ a ∥ b ( )
(3)∵ ∠2+∠4=____ (已知)
∴ a ∥ b ( )
=
同位角相等,两直线平行
=
内错角相等,两直线平行
180 °
同旁内角互补,两直线平行
c
a
b
1
2
3
4
回 忆
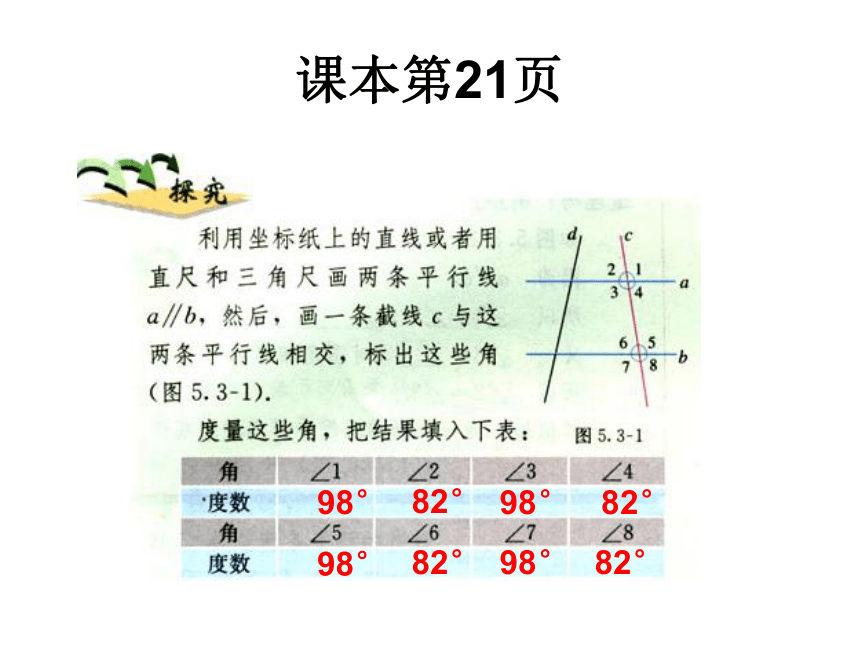
课本第21页
98°
98°
98°
98°
82°
82°
82°
82°
98°
98°
98°
98°
82°
82°
82°
82°
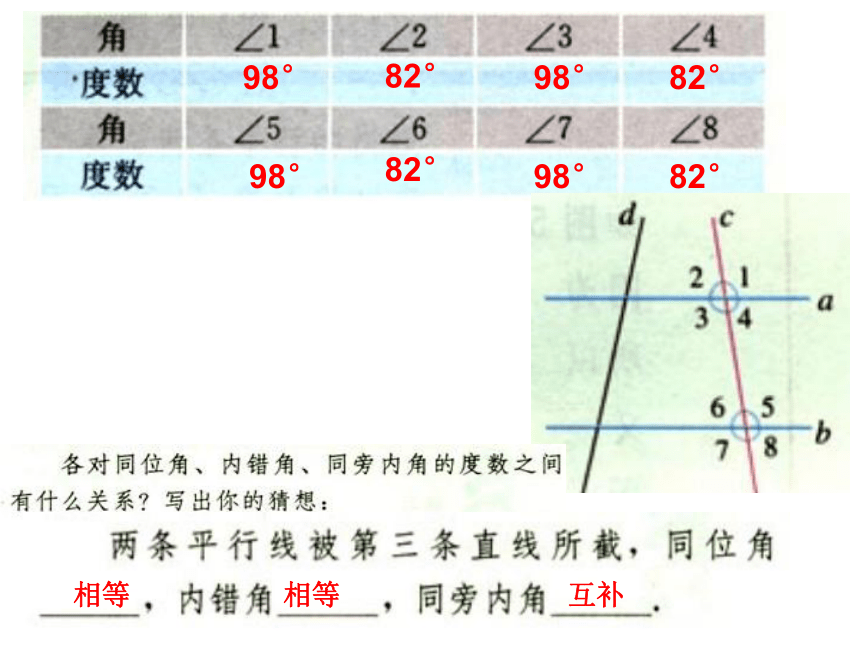
相等
相等
互补
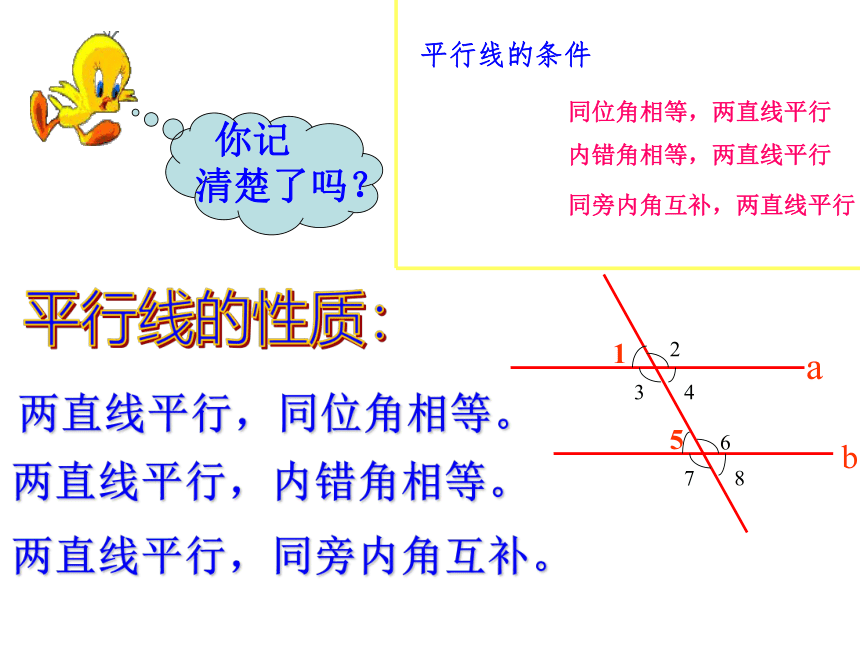
两直线平行,内错角相等。
两直线平行,同旁内角互补。
两直线平行,同位角相等。
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
你记
清楚了吗?
平行线的条件
a
b
1
5
2
3
4
6
7
8
你能根据性质1,说出性质2成立的道理吗
已知:a∥b,试说明:∠2=∠3
解:∵a∥b (已知)
∴ ∠1=∠2 ( )
又∵∠1=∠3 ( )
∴∠2=∠3
两直线平行,同位角相等.
对顶角相等
(等量代换)
∵∠1=∠5, ∴a∥b.
理由是____________________
(2) ∵ a∥b, ∴ ∠3=∠7.
理由是____________________
(3) ∵∠2=∠8, ∴a∥b.
理由是____________________
(4) ∵ a∥b, ∴ ∠3=∠5.
理由是____________________
(5) ∵∠2+∠5=180°, ∴a∥b.
理由是____________________
(6) ∵ a∥b, ∴ ∠3+∠8=180°.
理由是____________________
同位角相等,两直线平行.
两直线平行,同旁内角互补.
两直线平行,同位角相等.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
两直线平行,内错角相等.
b
a
1
5
2
3
4
6
7
8
课本第22页
解:
因为梯形的上、下两底互相平行,即:AB∥CD
所以∠A+∠D=180°
∠B+∠C=180°
(两直线平行,同旁内角互补)
又 ∠A=100°,∠B=115°
所以 ∠D=180°-∠A=180°-100°=80°
∠C=180°-∠B=180°-115°=65°
所以梯形的另外两个角分别是80°和65°。
课本第25页
答:36°,
因为两直线平行,内错角相等。
课本第25页
解:
∵AD∥BC (已知)
∴∠A+∠B=180°
(两直线平行,同旁内角互补)
又∵∠A=60° (已知)
∴∠B=180°- ∠A=180°- 60°=120°
图形
已知
结果
结论
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
图形
已知
结果
结论
同位角
内错角
同旁内角
a//b
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的判定
小结
a//b
同位角相等
两直线平行
a//b
平行线的判定与平行线 的性质的比较:
平行线的判定与平行线的性质是因果互换的两类不同的定理,
判定是说:满足了什么条件(性质)的两条直线是互相平行的
性质是说:如果两条直线平行,就应该具有什么性质。
平行线的识别
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补,两直线平行。
条件
结论
两直线平行,同旁内角互补。
平行线的特征
两直线平行,同位角相等;
两直线平行,内错角相等;
结论
条件
由两个角的相等或互补得到
直线的平行
由直线的平行得到
两个角的相等或互补
数量
位置
位置
数量
1、根据右边的图形,在括号内填上相应的理由:
(1)由于AB∥CD,根据 ,
可知∠3=∠C
(2)由于EC∥BD,根据 ,
可知∠3=∠B
(3)由于AB∥CD,根据 ,
可知∠2+∠C= 180°
A
C
D
B
E
1
2
3
4
两直线平行,内错角相等
两直线平行,同位角相等
两直线平行,同旁内角互补
如图,
(1)如果AD∥BC,那么∠B=∠1吗?
(2)如果AB∥CD,那么∠D=∠1吗?
解:由于AD∥BC,根据两直线平行,同位角相等,可知∠B=∠1。
例题讲解一
由于AB∥DC,根据两直线平行,内错角相等,可知∠D=∠1。
2.在图上画着与第三条直线相交的两条平 行线.如果∠1等于52°,那么∠2=____,∠3=____,∠4=_____。
1
4
2
3
52°
52°
128°
学习目标:
1、理解并熟记平行线的性质;
2、能够应用平行线的性质进行简单的推理和计算。
问题1:如图,
(1)∵ ∠1__∠2 (已知)
∴ a ∥ b ( )
(2)∵ ∠2____∠3 (已知)
∴ a ∥ b ( )
(3)∵ ∠2+∠4=____ (已知)
∴ a ∥ b ( )
=
同位角相等,两直线平行
=
内错角相等,两直线平行
180 °
同旁内角互补,两直线平行
c
a
b
1
2
3
4
回 忆
课本第21页
98°
98°
98°
98°
82°
82°
82°
82°
98°
98°
98°
98°
82°
82°
82°
82°
相等
相等
互补
两直线平行,内错角相等。
两直线平行,同旁内角互补。
两直线平行,同位角相等。
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
你记
清楚了吗?
平行线的条件
a
b
1
5
2
3
4
6
7
8
你能根据性质1,说出性质2成立的道理吗
已知:a∥b,试说明:∠2=∠3
解:∵a∥b (已知)
∴ ∠1=∠2 ( )
又∵∠1=∠3 ( )
∴∠2=∠3
两直线平行,同位角相等.
对顶角相等
(等量代换)
∵∠1=∠5, ∴a∥b.
理由是____________________
(2) ∵ a∥b, ∴ ∠3=∠7.
理由是____________________
(3) ∵∠2=∠8, ∴a∥b.
理由是____________________
(4) ∵ a∥b, ∴ ∠3=∠5.
理由是____________________
(5) ∵∠2+∠5=180°, ∴a∥b.
理由是____________________
(6) ∵ a∥b, ∴ ∠3+∠8=180°.
理由是____________________
同位角相等,两直线平行.
两直线平行,同旁内角互补.
两直线平行,同位角相等.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
两直线平行,内错角相等.
b
a
1
5
2
3
4
6
7
8
课本第22页
解:
因为梯形的上、下两底互相平行,即:AB∥CD
所以∠A+∠D=180°
∠B+∠C=180°
(两直线平行,同旁内角互补)
又 ∠A=100°,∠B=115°
所以 ∠D=180°-∠A=180°-100°=80°
∠C=180°-∠B=180°-115°=65°
所以梯形的另外两个角分别是80°和65°。
课本第25页
答:36°,
因为两直线平行,内错角相等。
课本第25页
解:
∵AD∥BC (已知)
∴∠A+∠B=180°
(两直线平行,同旁内角互补)
又∵∠A=60° (已知)
∴∠B=180°- ∠A=180°- 60°=120°
图形
已知
结果
结论
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
图形
已知
结果
结论
同位角
内错角
同旁内角
a//b
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的判定
小结
a//b
同位角相等
两直线平行
a//b
平行线的判定与平行线 的性质的比较:
平行线的判定与平行线的性质是因果互换的两类不同的定理,
判定是说:满足了什么条件(性质)的两条直线是互相平行的
性质是说:如果两条直线平行,就应该具有什么性质。
平行线的识别
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补,两直线平行。
条件
结论
两直线平行,同旁内角互补。
平行线的特征
两直线平行,同位角相等;
两直线平行,内错角相等;
结论
条件
由两个角的相等或互补得到
直线的平行
由直线的平行得到
两个角的相等或互补
数量
位置
位置
数量
1、根据右边的图形,在括号内填上相应的理由:
(1)由于AB∥CD,根据 ,
可知∠3=∠C
(2)由于EC∥BD,根据 ,
可知∠3=∠B
(3)由于AB∥CD,根据 ,
可知∠2+∠C= 180°
A
C
D
B
E
1
2
3
4
两直线平行,内错角相等
两直线平行,同位角相等
两直线平行,同旁内角互补
如图,
(1)如果AD∥BC,那么∠B=∠1吗?
(2)如果AB∥CD,那么∠D=∠1吗?
解:由于AD∥BC,根据两直线平行,同位角相等,可知∠B=∠1。
例题讲解一
由于AB∥DC,根据两直线平行,内错角相等,可知∠D=∠1。
2.在图上画着与第三条直线相交的两条平 行线.如果∠1等于52°,那么∠2=____,∠3=____,∠4=_____。
1
4
2
3
52°
52°
128°
