2.1.4函数的奇偶性[上学期]
文档属性
| 名称 | 2.1.4函数的奇偶性[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 190.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-28 10:08:00 | ||
图片预览





文档简介
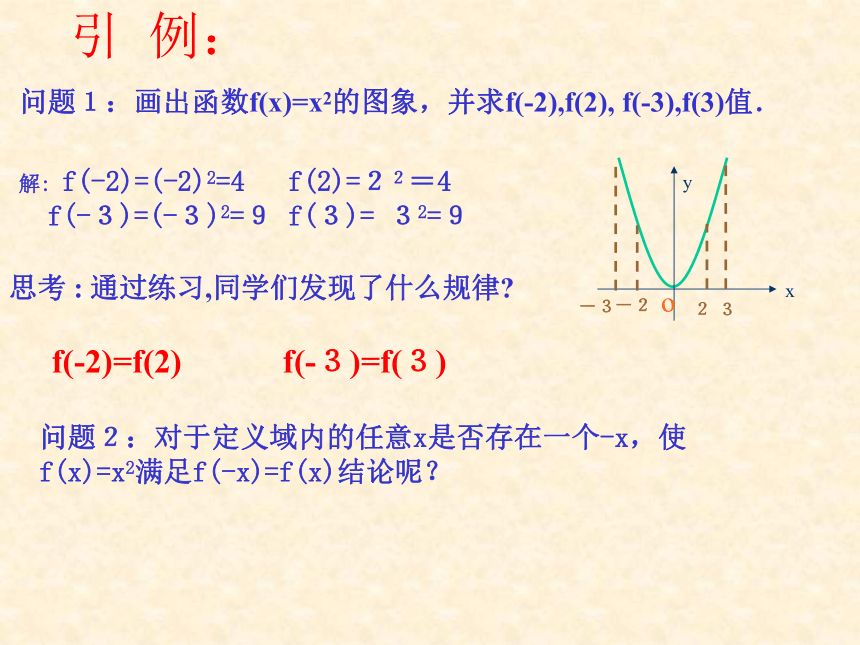
课件16张PPT。函数的奇偶性引 例:问题1:画出函数f(x)=x2的图象,并求f(-2),f(2), f(-3),f(3)值.解: f(-2)=(-2)2=4 f(2)=22=4
f(-3)=(-3)2=9 f(3)= 32=9
f(-2)=f(2) f(-3)=f(3)问题2:对于定义域内的任意x是否存在一个-x,使f(x)=x2满足f(-x)=f(x)结论呢?思考 : 通过练习,同学们发现了什么规律? 偶函数定义:
设函数y=f(x)的定义域为D,如果
对D内的任意一个x,都有-x D,且
f(-x)=f(x), 那么函数f(x)就叫
偶函数.
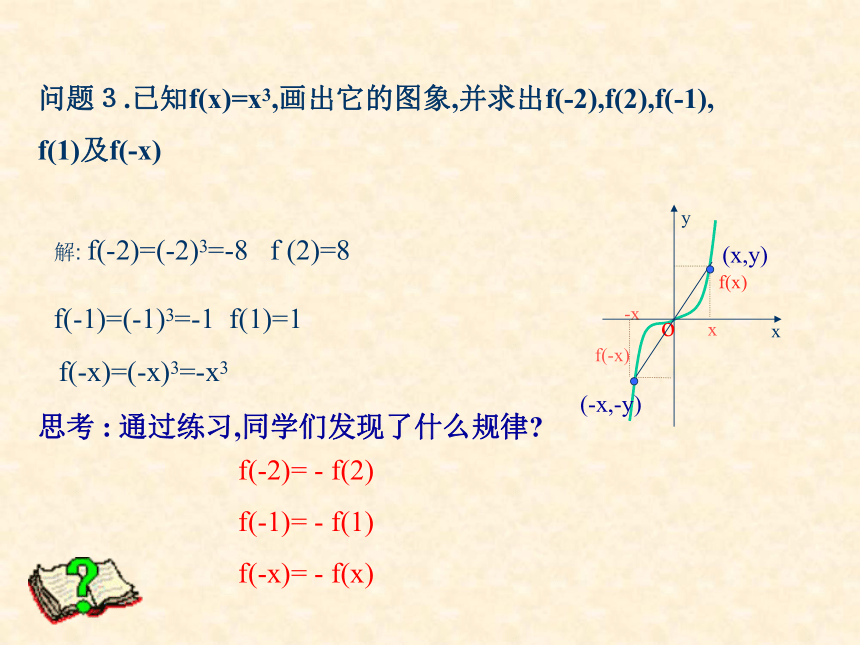
解: f(-2)=(-2)3=-8 f (2)=8f(-1)=(-1)3=-1 f(1)=1 f(-x)=(-x)3=-x3思考 : 通过练习,同学们发现了什么规律?f(-2)= - f(2)
f(-1)= - f(1)
f(-x)= - f(x)-xf(-x)xf(x)问题3.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),f(-1),
f(1)及f(-x) 奇函数定义:
设函数y=f(x)的定义域为D,如果
对D内的任意一个x,都有-x D,且
f(-x)=-f(x), 那么函数f(x)就叫做
奇函数.
☆对奇函数、偶函数定义的说明:(1).函数具有奇偶性的前提条件是定义域关于原点对称。 (2) 如果一个函数f(x)是奇函数或偶函数,那么我们就说
函数f(x) 具有奇偶性。问题4:
(1)定义在[-2,7]上的函数f(x)=x2是否是偶函数?为什么?
(2)定义在[-2,2]上的函数f(x)=x2是否是偶函数?为什么?
练习1. 说出下列函数的奇偶性:偶函数奇函数奇函数奇函数①f(x)=x4 ________ ④ f(x)= x -1 __________② f(x)=x ________奇函数⑤f(x)=x -2 __________偶函数③ f(x)=x5 __________⑥f(x)=x -3 _______________ 说明:对于形如 f(x)=x n 的函数,
若n为偶数,则它为偶函数。
若n为奇数,则它为奇函数。例1:判断下列函数的奇偶性(1) f(x)=x3+2x (2) f(x)=2x4+3x2解:∵f(-x)=(-x)3+2(-x)= -x3-2x= -(x3+2x)即 f(-x)= - f(x)∴f(x)为奇函数 ∵f(-x)=2(-x)4+3(-x)2=2x4+3x2∴f(x)为偶函数定义域为R解:定义域为R即 f(-x)= f(x) ⑴先求定义域,看是否关于原点对称;
☆ 说明:用定义判断函数奇偶性的步骤:⑵再判断f(-x)= -f(x)或f(-x)=f(x)
是否成立。练习2. 判断下列函数的奇偶性(3) f(x)=5(2) f(x)= x2 +2 x∈[-4,4)(4) f(x)=0奇函数的图象(如y=x3 )偶函数的图象(如y=x2)oaP/(-a ,f(-a))p(a ,f(a))-a(-a,-f(a))(-a,f(a))奇函数的图象(如y=x3 )偶函数的图象(如y=x2)oaP/(-a ,f(-a))p(a ,f(a))-a(-a,-f(a))(-a,f(a))奇偶函数图象的性质: ⑴ 奇函数的图象关于原点对称.
反之,如果一个函数的图象关于原点对称,那么这个函数是奇函数.⑵ 偶函数的图象关于y轴对称. 反之, 如果一个函数的图象关于 y 轴对称,那么这个函数是偶函数.注:奇偶函数图象的性质可用于:
①.简化函数图象的画法。
②.判断函数的奇偶性。oyx例2 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象。解:画法略本课小结:1.两个定义: 对于f(x)定义域内的任意一个x ,
如果都有f(-x)=-f(x) f(x)为奇函数。
如果都有f(-x)= f(x) f(x)为偶函数。2.两个性质:
一个函数为奇函数 它的图象关于原点对称。一个函数为偶函数 它的图象关于y 轴对称。 作业:
课本 P53 练习A1、2思考题:2.设y=f(x)为R上的任一函数,判断下列函数的奇偶性:
(1). F(x)=f(x)+f(- x) (2).F(x)=f(x)-f(-x)1.已知y=f(x)是偶函数,且在(-∞,0)上是增函数,则
y=f(x)在(0,∞)上是 ( )
A.增函数 B.减函数 C.非单调函数 D.单调性不确定3.具备下列条件之一的函数f(x)的奇偶性如何?
(1) f(x)+f(- x) =0 (2) f(x)-f(- x) =0
f(-3)=(-3)2=9 f(3)= 32=9
f(-2)=f(2) f(-3)=f(3)问题2:对于定义域内的任意x是否存在一个-x,使f(x)=x2满足f(-x)=f(x)结论呢?思考 : 通过练习,同学们发现了什么规律? 偶函数定义:
设函数y=f(x)的定义域为D,如果
对D内的任意一个x,都有-x D,且
f(-x)=f(x), 那么函数f(x)就叫
偶函数.
解: f(-2)=(-2)3=-8 f (2)=8f(-1)=(-1)3=-1 f(1)=1 f(-x)=(-x)3=-x3思考 : 通过练习,同学们发现了什么规律?f(-2)= - f(2)
f(-1)= - f(1)
f(-x)= - f(x)-xf(-x)xf(x)问题3.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),f(-1),
f(1)及f(-x) 奇函数定义:
设函数y=f(x)的定义域为D,如果
对D内的任意一个x,都有-x D,且
f(-x)=-f(x), 那么函数f(x)就叫做
奇函数.
☆对奇函数、偶函数定义的说明:(1).函数具有奇偶性的前提条件是定义域关于原点对称。 (2) 如果一个函数f(x)是奇函数或偶函数,那么我们就说
函数f(x) 具有奇偶性。问题4:
(1)定义在[-2,7]上的函数f(x)=x2是否是偶函数?为什么?
(2)定义在[-2,2]上的函数f(x)=x2是否是偶函数?为什么?
练习1. 说出下列函数的奇偶性:偶函数奇函数奇函数奇函数①f(x)=x4 ________ ④ f(x)= x -1 __________② f(x)=x ________奇函数⑤f(x)=x -2 __________偶函数③ f(x)=x5 __________⑥f(x)=x -3 _______________ 说明:对于形如 f(x)=x n 的函数,
若n为偶数,则它为偶函数。
若n为奇数,则它为奇函数。例1:判断下列函数的奇偶性(1) f(x)=x3+2x (2) f(x)=2x4+3x2解:∵f(-x)=(-x)3+2(-x)= -x3-2x= -(x3+2x)即 f(-x)= - f(x)∴f(x)为奇函数 ∵f(-x)=2(-x)4+3(-x)2=2x4+3x2∴f(x)为偶函数定义域为R解:定义域为R即 f(-x)= f(x) ⑴先求定义域,看是否关于原点对称;
☆ 说明:用定义判断函数奇偶性的步骤:⑵再判断f(-x)= -f(x)或f(-x)=f(x)
是否成立。练习2. 判断下列函数的奇偶性(3) f(x)=5(2) f(x)= x2 +2 x∈[-4,4)(4) f(x)=0奇函数的图象(如y=x3 )偶函数的图象(如y=x2)oaP/(-a ,f(-a))p(a ,f(a))-a(-a,-f(a))(-a,f(a))奇函数的图象(如y=x3 )偶函数的图象(如y=x2)oaP/(-a ,f(-a))p(a ,f(a))-a(-a,-f(a))(-a,f(a))奇偶函数图象的性质: ⑴ 奇函数的图象关于原点对称.
反之,如果一个函数的图象关于原点对称,那么这个函数是奇函数.⑵ 偶函数的图象关于y轴对称. 反之, 如果一个函数的图象关于 y 轴对称,那么这个函数是偶函数.注:奇偶函数图象的性质可用于:
①.简化函数图象的画法。
②.判断函数的奇偶性。oyx例2 已知函数y=f(x)是偶函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象。解:画法略本课小结:1.两个定义: 对于f(x)定义域内的任意一个x ,
如果都有f(-x)=-f(x) f(x)为奇函数。
如果都有f(-x)= f(x) f(x)为偶函数。2.两个性质:
一个函数为奇函数 它的图象关于原点对称。一个函数为偶函数 它的图象关于y 轴对称。 作业:
课本 P53 练习A1、2思考题:2.设y=f(x)为R上的任一函数,判断下列函数的奇偶性:
(1). F(x)=f(x)+f(- x) (2).F(x)=f(x)-f(-x)1.已知y=f(x)是偶函数,且在(-∞,0)上是增函数,则
y=f(x)在(0,∞)上是 ( )
A.增函数 B.减函数 C.非单调函数 D.单调性不确定3.具备下列条件之一的函数f(x)的奇偶性如何?
(1) f(x)+f(- x) =0 (2) f(x)-f(- x) =0
