导数的复习[下学期]
图片预览




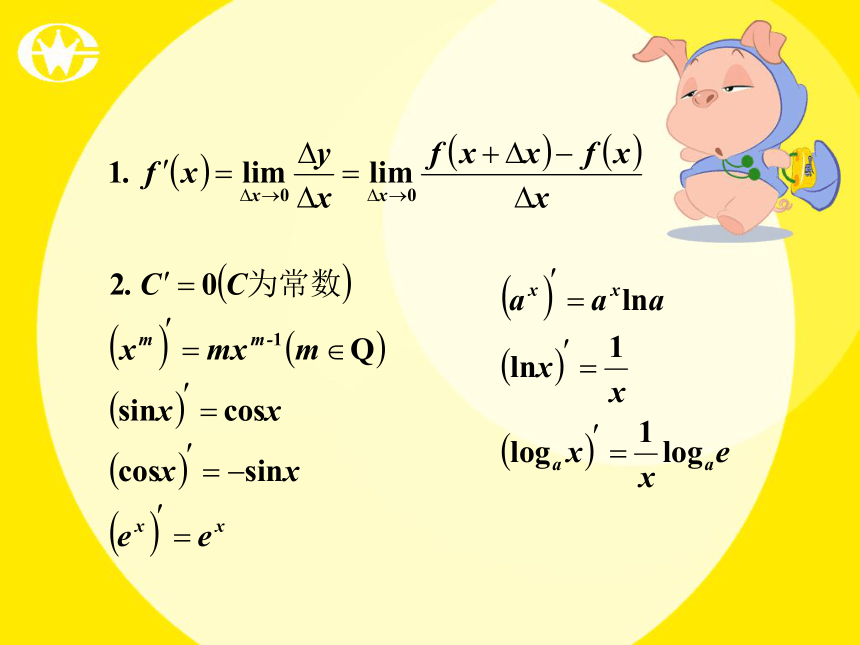
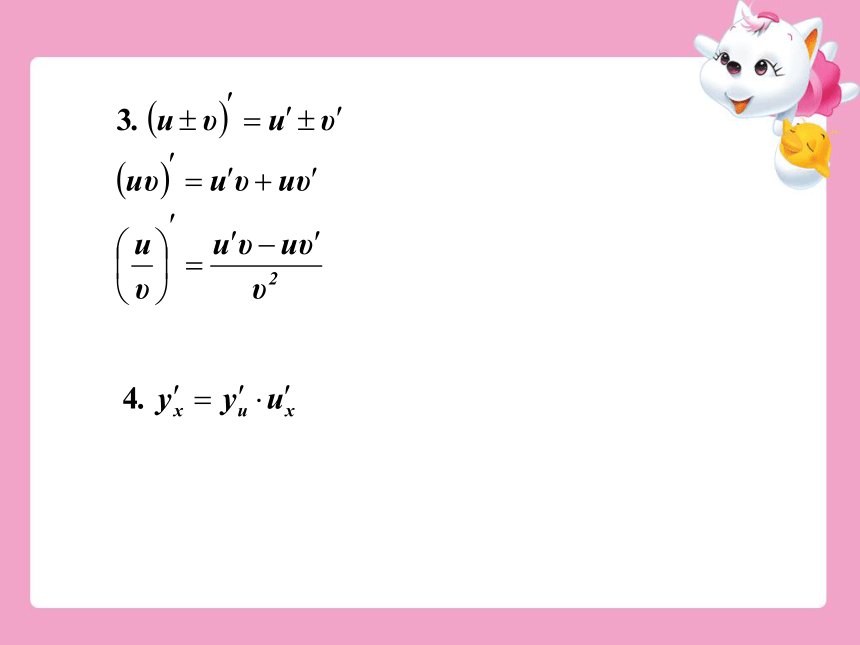
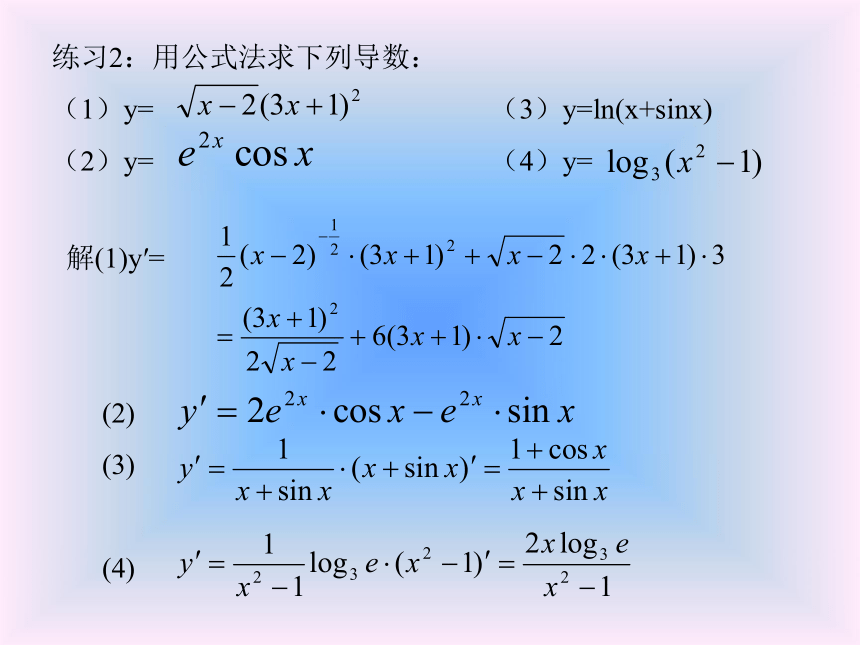


文档简介
课件22张PPT。1.3导数与定积分总结珠海市斗门区一中 郭俊峰
知识点总结:(一)对导数定义的理解;A:平均变化率 瞬时变化率B:割线斜率 切线斜率 C:其实质是从点x附近的平均变化率到点x的瞬时变化率;还要注意函数值的变化要与自变量的变化一致(1)设f(x)为可导函数,则
的为( )
B. 2 C. -2 D.0
(2)设f(x)在x=x0处可导,且
等于( )
1 B. 0 C. 3 D.1/3
(3)在 中,△x不能( )
A. 大于0 B.小于0 C. 等于0 D.小于0或等于0
CDB(二)怎样求 怎样求 ?(1)利用定义 注意步骤.(2)利用课本P14页基本函数的求导公式(3)对和,差,积,商的求导用课本P15公式(4)对复合函数的求导应该根据课本P17公式本节内容是本章最根本,最重要,最基本的内容练习2:用公式法求下列导数:
(1)y= (3)y=ln(x+sinx)
(2)y= (4)y=
解(1)y′=
(2)
(3)
(4)
(三)导数知识的最直接应用(1)由S(t)求v(x) 甚至求a(t)(2)求斜率,求切点,求切线方程,(已知y=f(x))A:已知斜率 k怎样求切点以及切线方程B:已知一点求切线斜率以及切线方程a,该点就是切点b,该点不是切点,是直线外一点函数 y=f(x) 在点x0处的导数的几何意义,就是曲线 y=f(x) 在点P(x0 ,f(x0)) 处的切线的斜率,1. 导数的几何意义 切线方程是 曲线 y=f(x)在点P(x0 ,f(x0))处的切线斜率是f ′(x0)3. 边际成本2. 导数的物理意义一般地,设C是成本,q是产量,成本与产量的函数关系式
C=C(q),函数C在q=q0处的导数就是C在q0处的边际成本,它表明当产量为q0时,增加单位产量需付出成本A. 练习
(1)曲线y=x4的斜率等于4的切线的方程为 .
(2)过曲线y=cosx上的点 且与过这点的切线垂直的
切线方程为 .
(3)一物体的运动方程是s=t2+3,则物体的初速度是 .
时间段(3,3+Δt)中,相应的平均是 .物体的
加速度是 . 在t=3时的瞬时速度等于 . 4x-y-3=006+△t26例1.求过点(2,0)且与曲线y= 相切的直线方程。解:设所求切线与曲线的切点为P(a,b)
∴
所求切线方程为
∵点(2,0)在切线上,代入整理,得a2b=2-a ------①
又∵P(a,b)在曲线 上,∴ab=1 ------------②
联立①,②解得 a=1,b=1
所求直线方程为 x+y-2=0
练习:
1.已知两条曲线y=x2-1与y=1-x3
(1)这两条曲线在x=x0的点处的切线互相平行,则x0= .
(2)这两条曲线在x=x1的点处的切线互相垂直,则x1= .
2.已知f(x)=cos2x ,则 .
3.已知函数y=x3的切线的斜率等于3,则其切线有 条. 0或42(四)怎样理解极点,极值;还有最值点,最值(应该学会结合原函数与其导函数图形理解)xx请你根据上面图象指出哪些是极点,极值;最值点,最值
(五)怎样求单调区间,极值,最值?步骤:1,求导函数2,求分界点注意不一定有解3,列表分析4,根据上面分析作出y=f(x)大致图象,指出极值点与极值5,比较极值与两个端点的函数值,找出最值点与最值要点·疑点·考点返回1. y=f(x)在(a,b)上可导,
若f′(x)>0,则f(x)为增函数,
若f′(x)<0,则f(x)为减函数2. 可导函数f(x)在极值点处的导数为0.3. f(x)在[a,b]上的最值求法:
①求出f(x)在(a,b)内的极值;
②将f(x)的各极值与f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.说明:
实际问题中,当已经明确所求极值为最大
或最小值时,只要由y′=0解得的极值点只有
一个,那么就有理由认为,这一极值点就是
最值点。
当然,如果是在一个闭区间上讨论的话,
还应关注端点取值大小.2.求曲线y=2x-x3在横坐标为-1的点处的切线l 。3.求y=2x3-x+1的单调递增区间是____________ 。1.已知y=x3-2x+1,则y′|x=2=_______ .3. 确定f(x)=xlnx的单调区间和极值。?4. 求函数f(x)=ln(1+x)-x2/4,在[0,2]上的最大值和最小值。?2. 已知f(x)=ln(2-x)+ax在(0,1)上是增函数,求:实数a的范围。?例3 求函数 的单调区间.解:时, y是减函数.例4 求函数 的极值.解:例5 求函数 的最大值和最小值.解:(六)优化问题 (1),读题,知道题目信息,找切入点(要解决的问题)(2)建模.宏观分析+微观分析(3)解题.参考前面怎样求最值(4)回归.最后答案要符合实际注意有些可以用不等式重要公式解决
知识点总结:(一)对导数定义的理解;A:平均变化率 瞬时变化率B:割线斜率 切线斜率 C:其实质是从点x附近的平均变化率到点x的瞬时变化率;还要注意函数值的变化要与自变量的变化一致(1)设f(x)为可导函数,则
的为( )
B. 2 C. -2 D.0
(2)设f(x)在x=x0处可导,且
等于( )
1 B. 0 C. 3 D.1/3
(3)在 中,△x不能( )
A. 大于0 B.小于0 C. 等于0 D.小于0或等于0
CDB(二)怎样求 怎样求 ?(1)利用定义 注意步骤.(2)利用课本P14页基本函数的求导公式(3)对和,差,积,商的求导用课本P15公式(4)对复合函数的求导应该根据课本P17公式本节内容是本章最根本,最重要,最基本的内容练习2:用公式法求下列导数:
(1)y= (3)y=ln(x+sinx)
(2)y= (4)y=
解(1)y′=
(2)
(3)
(4)
(三)导数知识的最直接应用(1)由S(t)求v(x) 甚至求a(t)(2)求斜率,求切点,求切线方程,(已知y=f(x))A:已知斜率 k怎样求切点以及切线方程B:已知一点求切线斜率以及切线方程a,该点就是切点b,该点不是切点,是直线外一点函数 y=f(x) 在点x0处的导数的几何意义,就是曲线 y=f(x) 在点P(x0 ,f(x0)) 处的切线的斜率,1. 导数的几何意义 切线方程是 曲线 y=f(x)在点P(x0 ,f(x0))处的切线斜率是f ′(x0)3. 边际成本2. 导数的物理意义一般地,设C是成本,q是产量,成本与产量的函数关系式
C=C(q),函数C在q=q0处的导数就是C在q0处的边际成本,它表明当产量为q0时,增加单位产量需付出成本A. 练习
(1)曲线y=x4的斜率等于4的切线的方程为 .
(2)过曲线y=cosx上的点 且与过这点的切线垂直的
切线方程为 .
(3)一物体的运动方程是s=t2+3,则物体的初速度是 .
时间段(3,3+Δt)中,相应的平均是 .物体的
加速度是 . 在t=3时的瞬时速度等于 . 4x-y-3=006+△t26例1.求过点(2,0)且与曲线y= 相切的直线方程。解:设所求切线与曲线的切点为P(a,b)
∴
所求切线方程为
∵点(2,0)在切线上,代入整理,得a2b=2-a ------①
又∵P(a,b)在曲线 上,∴ab=1 ------------②
联立①,②解得 a=1,b=1
所求直线方程为 x+y-2=0
练习:
1.已知两条曲线y=x2-1与y=1-x3
(1)这两条曲线在x=x0的点处的切线互相平行,则x0= .
(2)这两条曲线在x=x1的点处的切线互相垂直,则x1= .
2.已知f(x)=cos2x ,则 .
3.已知函数y=x3的切线的斜率等于3,则其切线有 条. 0或42(四)怎样理解极点,极值;还有最值点,最值(应该学会结合原函数与其导函数图形理解)xx请你根据上面图象指出哪些是极点,极值;最值点,最值
(五)怎样求单调区间,极值,最值?步骤:1,求导函数2,求分界点注意不一定有解3,列表分析4,根据上面分析作出y=f(x)大致图象,指出极值点与极值5,比较极值与两个端点的函数值,找出最值点与最值要点·疑点·考点返回1. y=f(x)在(a,b)上可导,
若f′(x)>0,则f(x)为增函数,
若f′(x)<0,则f(x)为减函数2. 可导函数f(x)在极值点处的导数为0.3. f(x)在[a,b]上的最值求法:
①求出f(x)在(a,b)内的极值;
②将f(x)的各极值与f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.说明:
实际问题中,当已经明确所求极值为最大
或最小值时,只要由y′=0解得的极值点只有
一个,那么就有理由认为,这一极值点就是
最值点。
当然,如果是在一个闭区间上讨论的话,
还应关注端点取值大小.2.求曲线y=2x-x3在横坐标为-1的点处的切线l 。3.求y=2x3-x+1的单调递增区间是____________ 。1.已知y=x3-2x+1,则y′|x=2=_______ .3. 确定f(x)=xlnx的单调区间和极值。?4. 求函数f(x)=ln(1+x)-x2/4,在[0,2]上的最大值和最小值。?2. 已知f(x)=ln(2-x)+ax在(0,1)上是增函数,求:实数a的范围。?例3 求函数 的单调区间.解:时, y是减函数.例4 求函数 的极值.解:例5 求函数 的最大值和最小值.解:(六)优化问题 (1),读题,知道题目信息,找切入点(要解决的问题)(2)建模.宏观分析+微观分析(3)解题.参考前面怎样求最值(4)回归.最后答案要符合实际注意有些可以用不等式重要公式解决
