函数2[上学期]

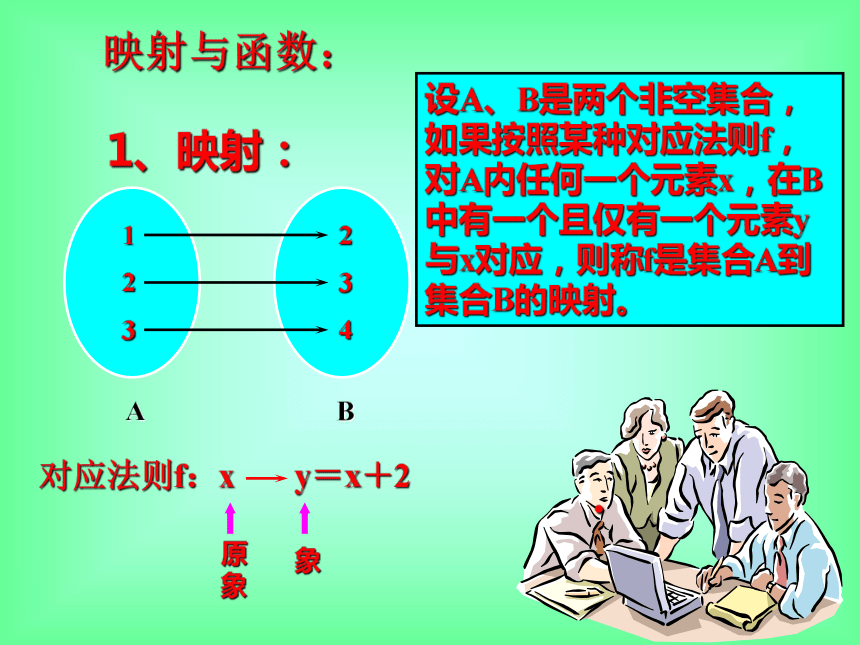
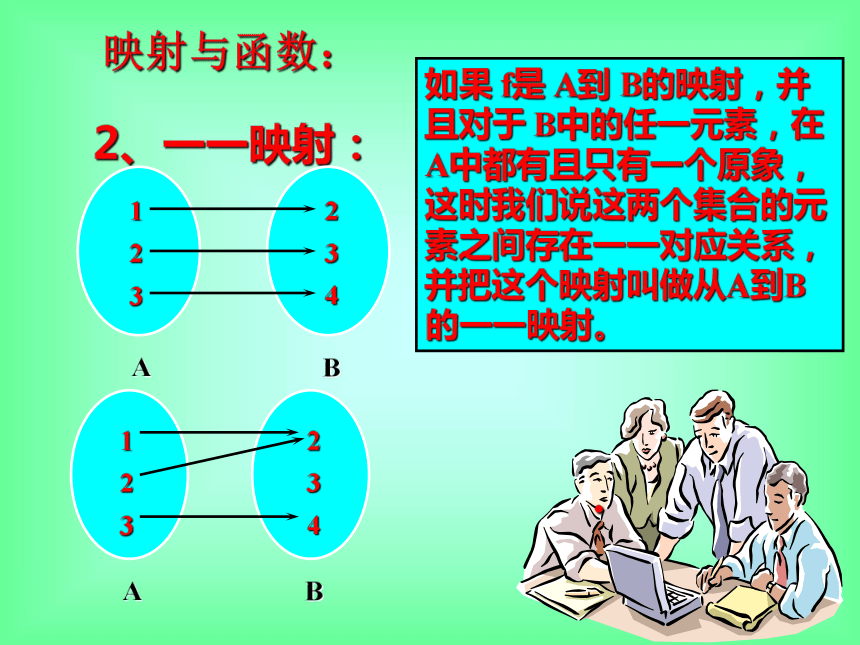
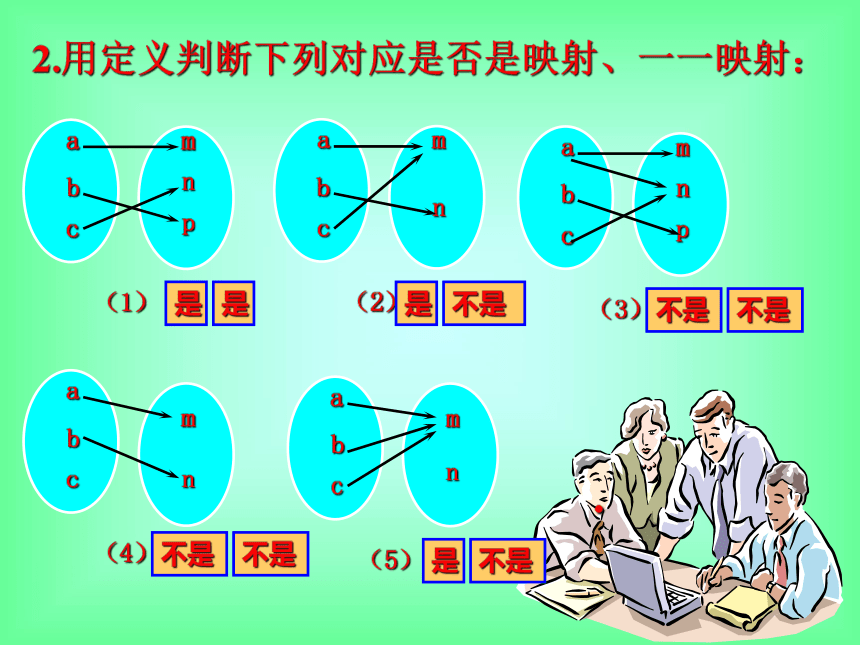
课件15张PPT。教者： guoyumin函 数（二）1. 什么是函数？如何从集合的角度出发来定义函数？复习与提问：2. 函数的三要素是什么？它们之间有什么联系？.映射与函数：1、映射：设A、B是两个非空集合，如果按照某种对应法则f，对A内任何一个元素x，在B中有一个且仅有一个元素y与x对应，则称f是集合A到集合B的映射。原象象.映射与函数：2、一一映射：如果 f是 A到 B的映射，并且对于 B中的任一元素，在 A中都有且只有一个原象，这时我们说这两个集合的元素之间存在一一对应关系，并把这个映射叫做从A到B的一一映射。.2.用定义判断下列对应是否是映射、一一映射：是是不是不是是a是不是不是不是不是课堂练习：1. P39 练习A、练习B▲求下列函数的定义域：综合练习：{x | x≠1且x≠－3}{x | x＞3 }▲下列各组函数中，哪组函数是相同的函数？××∨∨▲已知函数f(x)＝3x＋2，
求f(x－2),f(x2＋x-1) f (x－2）＝3x－4，f (x2＋x－1)＝3x2＋3x－1。▲已知函数f(x－2)＝3x－4，
求f(x),f(x＋2) f (x）＝3x＋2，f (x＋2)＝3x＋8。▲已知函数f(x)的定义域是[1，2]，则函数f（x＋1）的定义域是（ ）（A）[1，2] （B）[0，1] （C）[2，3] （D）不能确定 B ▲已知函数f(x＋1)的定义域是[0，1]，则函数f（x）的定义域是（ ）（A）[1，2] （B）[0，1] （C）[2，3] （D）不能确定 A ▲已知函数f(x)＝2x－3，g(x)＝x2，求f(x＋2),g(1-x),f[g(x)],g[f(x)]f (x＋2）＝2x＋1，g (1－x)＝(1－x)2，f [ g(x) ]＝2x2＋1，g [ f(x) ]＝(2x－3)2，f (x）＝x2－2课后作业：
再 见