导数的运算法则与四则运算[下学期]
文档属性
| 名称 | 导数的运算法则与四则运算[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 82.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-20 00:00:00 | ||
图片预览

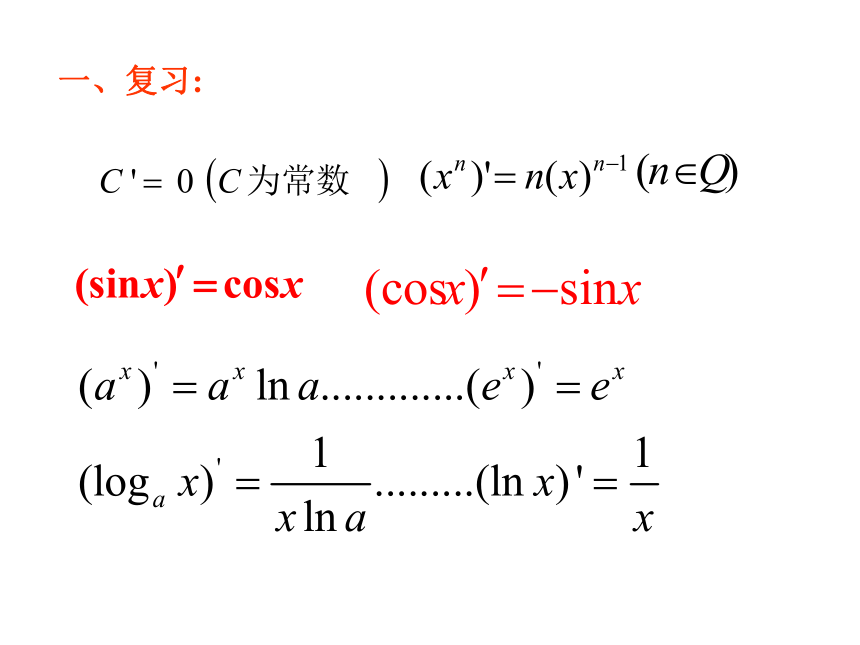



文档简介
课件10张PPT。导数的运算法则
复合函数的导数一、复习:二、导数的运算法则:(和差积商的导数)(可以推广到求有限个函数的和(差)的导数.)(轮流求导之和)(上导乘下,下导乘上,差比下方)课本p15 例3例1 求函数三、例题分析对于函数求导,一般要遵循先化简再求导的基本原则。四、复合函数及求导法则:一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记为复合函数的导数:y对x的导数=y对u的导数与u对x的导数的乘积例4 求下列函数的导数补充:例2:设f(x)可导,求下列函数的导数:
(1)f(x2);(2)f( );(3)f(sin2x)+f(cos2x)解: 说明:对于抽象函数的求导,一方面要从其形式是把握其 结构特征,另一方面要充分运用复合关系的求导法则.小结:1、导数的四则运算法则:2、复合函数及求导法则:y对x的导数=y对u的导数与u对x的导数的乘积(灵活选取中间变量,勿忘中间变量对自变量的求导)
复合函数的导数一、复习:二、导数的运算法则:(和差积商的导数)(可以推广到求有限个函数的和(差)的导数.)(轮流求导之和)(上导乘下,下导乘上,差比下方)课本p15 例3例1 求函数三、例题分析对于函数求导,一般要遵循先化简再求导的基本原则。四、复合函数及求导法则:一般地,对于两个函数y=f(u)和u=g(x),如果通过变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记为复合函数的导数:y对x的导数=y对u的导数与u对x的导数的乘积例4 求下列函数的导数补充:例2:设f(x)可导,求下列函数的导数:
(1)f(x2);(2)f( );(3)f(sin2x)+f(cos2x)解: 说明:对于抽象函数的求导,一方面要从其形式是把握其 结构特征,另一方面要充分运用复合关系的求导法则.小结:1、导数的四则运算法则:2、复合函数及求导法则:y对x的导数=y对u的导数与u对x的导数的乘积(灵活选取中间变量,勿忘中间变量对自变量的求导)
