函数(一) [上下学期通用]
图片预览


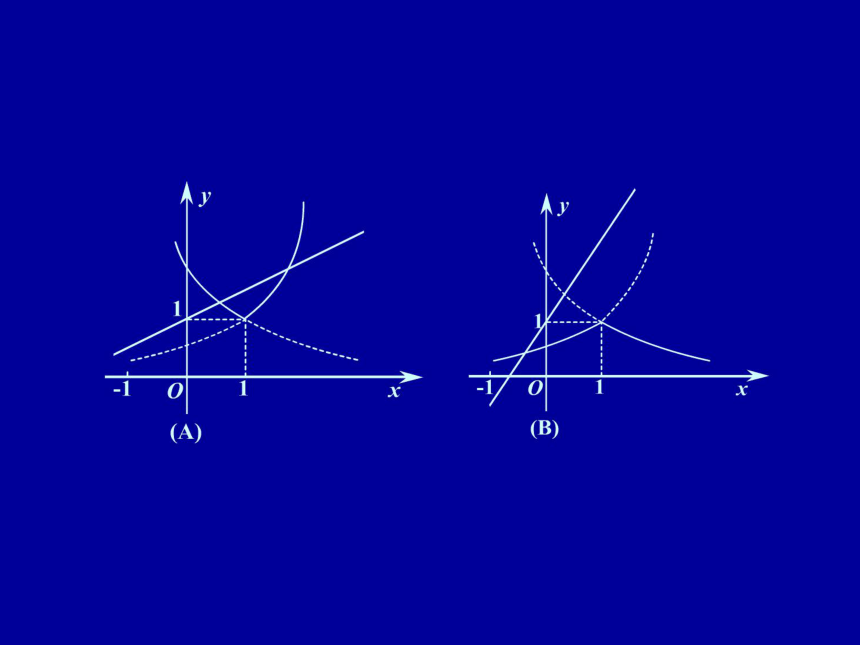








文档简介
课件65张PPT。分析:
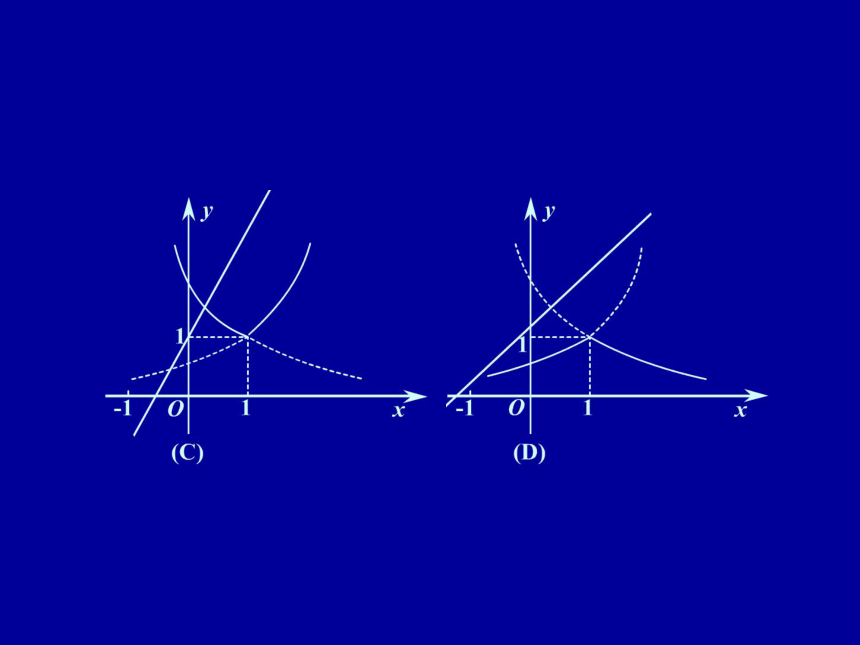
(A)曲线?a>1,直线? 0 (B)曲线?01;
(D)直线?纵截距大于1.
故(C)正确. 例2 函数y = f ( x ) 对任意实数x,总有
(1)f (a-x) = f ( b + x ),这里
a,b是常数,问函数的图像有什么性质,证明你的结论;
(2)f (a-x) =-f ( b + x ),这里a,b是常数,问函数的图像有什么性质,证明你的结论. 例3
不等式y = lg ( | x-2 | + | x + 8 | ) < a 的解集是空集,那么a的取值范围是________. 解:易知函数y=lg(| x-2 |+|x + 8| )的最小值存在,因此,不等式无解相当于a≤ymin.
|x-2|+|x + 8| 表示数轴上的点x,到点2和-8的距离之和,
∴ | x-2 | + | x + 8 | ≥ 10
∴ lg ( | x-2 | + | x + 8 | ) ≥1
于是a≤1时,不等式解集为? ,反之亦然. 例6 已知f ( x )=-x2 + 2x + 8,
g ( x ) = f ( 2-x 2 ),求g ( x )的单调增区间.
【讲解】很明显这是一个复合函数的单调性问题,所以应“分层剥离”为两个函数
t=-x2+2 ①
y = f ( t ) =-t 2 + 2t + 8 ② 例7 f ( x )是奇函数,x>0时,
f ( x ) = x · (4-3x),那么x<0时
f ( x ) = _______. 【解法2】 设x<0,则-x>0
∴ f (-x) = (-x)·(4 + 3x)
∵ f ( x )是奇函数,
∴ f (-x) = -f ( x )
∴ x<0时,f ( x ) =-f (-x )=x(4+3x).于是
f ( a )+f (-a ) = 2 f ( 0 )·f ( a ) = f ( a )
∴ f (-a ) = f ( a ),a∈R
∴ f ( x )是R上的偶函数.
而f ( 0 )≠0,故f ( x )不是奇函数.
应选(B). 例10 已知函数f ( x ),对任意实数x,有下面四个关系式成立:
(1)f ( x ) =-f (x+a)(a为非零常数);
(2)f ( x ) = f (a-x)(a为非零常数);
(3)f (a-x) = f (b-x)(a,b为常数且a2 + b2≠0) (4)f (a-x) =-f (b-x)(a,b为常数且a2+b2≠0)
其中使f ( x )是周期函数的关系式是_______. 【解】考查(1),f ( x )=-f (x+a)说明“两个自变数相差a,则函数值互为相反数”,于是相差2a时,函数值相等:
f ( x )=-f (x+a) = f (x+2a)
∴ 等式(1)使f ( x )是周期函数,
且2a是周期; 考查(4),f (a-x) =-f (b-x)表明自变数相差a-b时,函数值互为相反数,于是相差2(a-b)时,函数值相等.故(4)同(1),能使 f ( x )为周期函数,且 2(a-b)是周期.
综上所述,应填(1),(3),(4). 例12 f (x)是R上的奇函数,且对任何实数x,总有f (x+2)=-f (x),且x?[0,1]时,f (x)=x,则f (x)在R上的解析式为 . 【解】∵ f (x+2)=-f (x),
∴ f (x+4)=-f (x+2)=f (x),
∴ f (x)是周期函数,4是周期.
∵ f (-x)=-f (x).
∴ f (x+2)=f (-x),
∴ f (x)的图像关于x=1对称,
由上述这些性质,及x?[0,1]时,y=x,
得知f (x)的图像如下:【解】∵y=f (x)的图像关于x=0
对称, ∴ f ( x )=f (-x),
∵ y=f (x)的图像关于x=2对称,
∴ f (-x)=f (4+x).
于是有f ( x )=f (4+x)
∴ f ( x )是周期为4的函数,
当-2≤x≤0时,
0≤-x≤2且-x + 4∈[4,6] ∵ y=f (x)的图像关于x=0对称,
∴ f (x)=f (-x).∵ 周期为4,
∴ f (-x)=f (-x+4)=2-x+4 +1
即在 [-2,0]上,y=f (x)=2-x+4 +1
∴ 2-x+4=y-1
-x+4=log2(y-1)
x=4-log2(y-1)
∴ [-2,0] 上,f (x)=4-log2(x-1)
应选(B). 【分析】很明显,g(x)是f -1(x+1)的反函数.只要求出f -1(x+1)的反函数解析式,就得到g ( x ),不难得到g ( 5 ).
f -1(x+1)的反函数不是f (x+1),为什么?看了下面的解法,应当能回答出来. 【解法2】y=f (x)和f -1(x)的图像关于x=y对称,当f -1(x)沿x轴负方向平移1个单位时,“镜子” y=x另一侧的“像” f (x)沿y轴负方向平移1个单位,于是
f -1(x+1)和f (x)-1互为反函数.
即g (x)=f (x)-1,下略.
(A)曲线?a>1,直线? 0
(D)直线?纵截距大于1.
故(C)正确. 例2 函数y = f ( x ) 对任意实数x,总有
(1)f (a-x) = f ( b + x ),这里
a,b是常数,问函数的图像有什么性质,证明你的结论;
(2)f (a-x) =-f ( b + x ),这里a,b是常数,问函数的图像有什么性质,证明你的结论. 例3
不等式y = lg ( | x-2 | + | x + 8 | ) < a 的解集是空集,那么a的取值范围是________. 解:易知函数y=lg(| x-2 |+|x + 8| )的最小值存在,因此,不等式无解相当于a≤ymin.
|x-2|+|x + 8| 表示数轴上的点x,到点2和-8的距离之和,
∴ | x-2 | + | x + 8 | ≥ 10
∴ lg ( | x-2 | + | x + 8 | ) ≥1
于是a≤1时,不等式解集为? ,反之亦然. 例6 已知f ( x )=-x2 + 2x + 8,
g ( x ) = f ( 2-x 2 ),求g ( x )的单调增区间.
【讲解】很明显这是一个复合函数的单调性问题,所以应“分层剥离”为两个函数
t=-x2+2 ①
y = f ( t ) =-t 2 + 2t + 8 ② 例7 f ( x )是奇函数,x>0时,
f ( x ) = x · (4-3x),那么x<0时
f ( x ) = _______. 【解法2】 设x<0,则-x>0
∴ f (-x) = (-x)·(4 + 3x)
∵ f ( x )是奇函数,
∴ f (-x) = -f ( x )
∴ x<0时,f ( x ) =-f (-x )=x(4+3x).于是
f ( a )+f (-a ) = 2 f ( 0 )·f ( a ) = f ( a )
∴ f (-a ) = f ( a ),a∈R
∴ f ( x )是R上的偶函数.
而f ( 0 )≠0,故f ( x )不是奇函数.
应选(B). 例10 已知函数f ( x ),对任意实数x,有下面四个关系式成立:
(1)f ( x ) =-f (x+a)(a为非零常数);
(2)f ( x ) = f (a-x)(a为非零常数);
(3)f (a-x) = f (b-x)(a,b为常数且a2 + b2≠0) (4)f (a-x) =-f (b-x)(a,b为常数且a2+b2≠0)
其中使f ( x )是周期函数的关系式是_______. 【解】考查(1),f ( x )=-f (x+a)说明“两个自变数相差a,则函数值互为相反数”,于是相差2a时,函数值相等:
f ( x )=-f (x+a) = f (x+2a)
∴ 等式(1)使f ( x )是周期函数,
且2a是周期; 考查(4),f (a-x) =-f (b-x)表明自变数相差a-b时,函数值互为相反数,于是相差2(a-b)时,函数值相等.故(4)同(1),能使 f ( x )为周期函数,且 2(a-b)是周期.
综上所述,应填(1),(3),(4). 例12 f (x)是R上的奇函数,且对任何实数x,总有f (x+2)=-f (x),且x?[0,1]时,f (x)=x,则f (x)在R上的解析式为 . 【解】∵ f (x+2)=-f (x),
∴ f (x+4)=-f (x+2)=f (x),
∴ f (x)是周期函数,4是周期.
∵ f (-x)=-f (x).
∴ f (x+2)=f (-x),
∴ f (x)的图像关于x=1对称,
由上述这些性质,及x?[0,1]时,y=x,
得知f (x)的图像如下:【解】∵y=f (x)的图像关于x=0
对称, ∴ f ( x )=f (-x),
∵ y=f (x)的图像关于x=2对称,
∴ f (-x)=f (4+x).
于是有f ( x )=f (4+x)
∴ f ( x )是周期为4的函数,
当-2≤x≤0时,
0≤-x≤2且-x + 4∈[4,6] ∵ y=f (x)的图像关于x=0对称,
∴ f (x)=f (-x).∵ 周期为4,
∴ f (-x)=f (-x+4)=2-x+4 +1
即在 [-2,0]上,y=f (x)=2-x+4 +1
∴ 2-x+4=y-1
-x+4=log2(y-1)
x=4-log2(y-1)
∴ [-2,0] 上,f (x)=4-log2(x-1)
应选(B). 【分析】很明显,g(x)是f -1(x+1)的反函数.只要求出f -1(x+1)的反函数解析式,就得到g ( x ),不难得到g ( 5 ).
f -1(x+1)的反函数不是f (x+1),为什么?看了下面的解法,应当能回答出来. 【解法2】y=f (x)和f -1(x)的图像关于x=y对称,当f -1(x)沿x轴负方向平移1个单位时,“镜子” y=x另一侧的“像” f (x)沿y轴负方向平移1个单位,于是
f -1(x+1)和f (x)-1互为反函数.
即g (x)=f (x)-1,下略.
