苏教版(2019)高中数学选择性必修第二册课件 8.3正态分布 课件(共15张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第二册课件 8.3正态分布 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 381.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
8.3正态分布
学习目标
1.了解正态分布在实际生活中的意义和作用;
2.掌握正态分布的特点及正态分布曲线所表示的意义、性质;
3.掌握正态分布3-σ原则及实际应用.
情景创设
问题:上述数据的分布有怎样的特点?
通过频率分布直方图来分析数据:
区间号 区间 频数 频率 累积频率 频率/组距
1 153.5~157.5 5 0.0595 0.0595 0.015
2 157.5~161.5 8 0.0952 0.1547 0.024
3 161.5~165.5 10 0.1190 0.2738 0.030
4 165.5~169.5 15 0.1786 0.4534 0.045
5 169.5~173.5 18 0.2143 0.6667 0.054网]
6 173.5~1775 18 0.1786 0.8452 0.045
7 177.5~181.5 8 0.0952 0.9405 0.024
8 181.5~185.5 5 0.0595 1 0.015
通过频率分布表来分析数据:组数、组距
x
y
数学建构
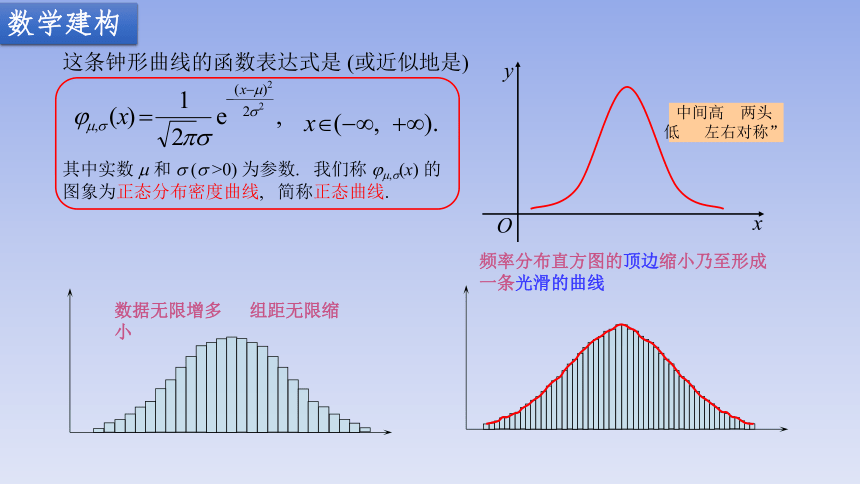
数据无限增多 组距无限缩小
中间高 两头低 左右对称”
频率分布直方图的顶边缩小乃至形成一条光滑的曲线
这条钟形曲线的函数表达式是 (或近似地是)
O
x
y
x (-∞, +∞).
其中实数 m 和 s (s >0) 为参数. 我们称 jm,s(x) 的图象为正态分布密度曲线, 简称正态曲线.
数学建构
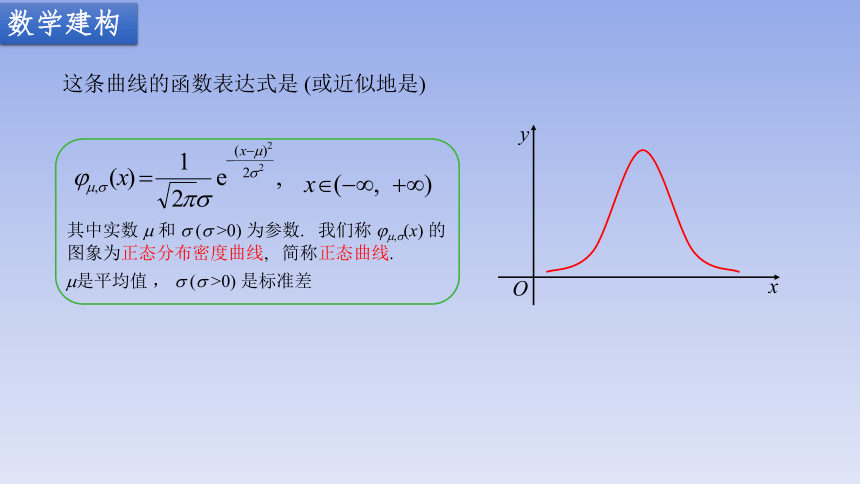
这条曲线的函数表达式是 (或近似地是)
O
x
y
x (-∞, +∞)
其中实数 m 和 s (s >0) 为参数. 我们称 jm,s(x) 的图象为正态分布密度曲线, 简称正态曲线.
m是平均值 , s (s >0) 是标准差
数学探究
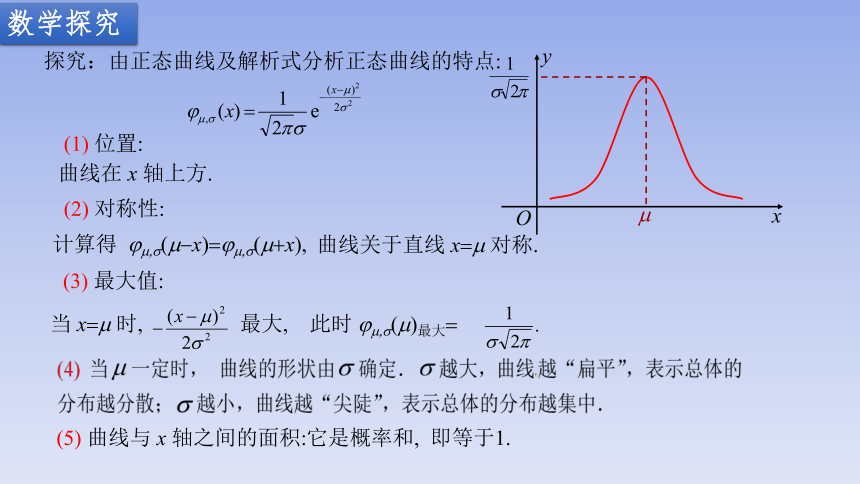
探究:由正态曲线及解析式分析正态曲线的特点:
O
x
y
m
(1) 位置:
曲线在 x 轴上方.
(2) 对称性:
计算得 jm,s(m-x)=jm,s(m+x),
曲线关于直线 x=m 对称.
(3) 最大值:
当 x=m 时, 最大,
此时 jm,s(m)最大=
(5) 曲线与 x 轴之间的面积:它是概率和, 即等于1.
数学应用
例1. 设两个正态分布 N(m1, s12) (s1>0) 和N(m2, s22) (s2>0) 的密度函数图象如图所示, 则有 ( )
(A) m1s2 (C) m1>m2, s1m2, s1>s2
x
y
O
0.5
1.0
-0.5
-1.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
N(m1, s12)
N(m2, s22)
分析:
∵ x=m 是对称轴,
∴m1s 确定峰值,
当 x=m 时,
s 越大, 峰值越小.
∴s1A
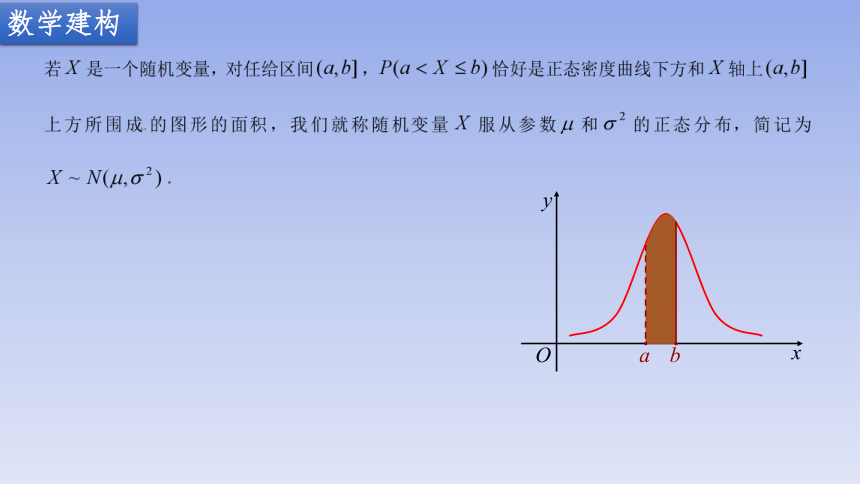
数学建构
O
x
y
a
b
数学应用
例2. 已知随机变量 x 服从正态分布 N(0, s2). 若 P(x>2)=0.023, 则 P(-2≤x≤2) 等于 ( )
(A) 0.477 (B) 0.628 (C) 0.954 (D) 0.977
x
y
O
2
-2
分析:
由 N(0, s2) 知
x=m=0 是对称轴 (如图).
∵ P(x>2)=0.023,
∴ P(x<-2)=0.023.
则 P(-2≤x≤2)=1-2 0.023
=0.954.
C
数学建构
特别地
P(m-sP(m-2sP(m-3sX 在 (m-3s, m+3s] 以外, 概率非常小, 在这种情况下, 一次试验中事件几乎不可能发生.
m
m-s
m+s
m
m-2s
m+2s
m
m-3s
m+3s
数学应用
例3. 某地区数学考试的成绩 X 服从正态分布, 其密度曲线如图所示, 成绩 X 位于区间 (52, 68] 的概率是多少
O
x
y
60
20
40
80
100
解:
由图知
m=60, s=8,
52=m-s, 68=m+s,
∴P(520.6826.
数学建构
数学应用
例4. 若 X~N(5, 1), 求 P(6解:
由 X~N(5, 1) 知 m=5, s =1.
∴P(5-1则 P(5同理,
P(5-2∴ P(5于是得 P(6=0.4772-0.3413
=0.1359.
课堂小结
x (-∞, +∞).
正态分布密度曲线
通过频率分布直方图
x
y
O
x
y
O
x
y
a
b
正态分布
课堂小结
课堂达标
1. 若 X~N(m, s2), 则 X 位于区域 (m, m+s] 内的概率是多少
解:
若 X~N(m, s2), 则
P(m-s因为正态曲线关于直线 x=m 对称,
所以 P(m2. 标准正态分布密度函数为
(1) 证明 f(x) 是偶函数;
(2) 求 f(x) 的最大值;
(3) 利用指数函数的性质说明 f(x) 的增减性.
(1)
证明:
=f(x),
∴f(x)是偶函数.
且定义域关于 x=0 对称,
(2)
解:
由解析式知 m=0,s =1,
∴ f(x) 的最大值是 f(0)
(3) f(x) 在 (-∞, 0] 上是增函数, 在 [0, +∞) 上是减函数.
8.3正态分布
学习目标
1.了解正态分布在实际生活中的意义和作用;
2.掌握正态分布的特点及正态分布曲线所表示的意义、性质;
3.掌握正态分布3-σ原则及实际应用.
情景创设
问题:上述数据的分布有怎样的特点?
通过频率分布直方图来分析数据:
区间号 区间 频数 频率 累积频率 频率/组距
1 153.5~157.5 5 0.0595 0.0595 0.015
2 157.5~161.5 8 0.0952 0.1547 0.024
3 161.5~165.5 10 0.1190 0.2738 0.030
4 165.5~169.5 15 0.1786 0.4534 0.045
5 169.5~173.5 18 0.2143 0.6667 0.054网]
6 173.5~1775 18 0.1786 0.8452 0.045
7 177.5~181.5 8 0.0952 0.9405 0.024
8 181.5~185.5 5 0.0595 1 0.015
通过频率分布表来分析数据:组数、组距
x
y
数学建构
数据无限增多 组距无限缩小
中间高 两头低 左右对称”
频率分布直方图的顶边缩小乃至形成一条光滑的曲线
这条钟形曲线的函数表达式是 (或近似地是)
O
x
y
x (-∞, +∞).
其中实数 m 和 s (s >0) 为参数. 我们称 jm,s(x) 的图象为正态分布密度曲线, 简称正态曲线.
数学建构
这条曲线的函数表达式是 (或近似地是)
O
x
y
x (-∞, +∞)
其中实数 m 和 s (s >0) 为参数. 我们称 jm,s(x) 的图象为正态分布密度曲线, 简称正态曲线.
m是平均值 , s (s >0) 是标准差
数学探究
探究:由正态曲线及解析式分析正态曲线的特点:
O
x
y
m
(1) 位置:
曲线在 x 轴上方.
(2) 对称性:
计算得 jm,s(m-x)=jm,s(m+x),
曲线关于直线 x=m 对称.
(3) 最大值:
当 x=m 时, 最大,
此时 jm,s(m)最大=
(5) 曲线与 x 轴之间的面积:它是概率和, 即等于1.
数学应用
例1. 设两个正态分布 N(m1, s12) (s1>0) 和N(m2, s22) (s2>0) 的密度函数图象如图所示, 则有 ( )
(A) m1
x
y
O
0.5
1.0
-0.5
-1.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
N(m1, s12)
N(m2, s22)
分析:
∵ x=m 是对称轴,
∴m1
当 x=m 时,
s 越大, 峰值越小.
∴s1
数学建构
O
x
y
a
b
数学应用
例2. 已知随机变量 x 服从正态分布 N(0, s2). 若 P(x>2)=0.023, 则 P(-2≤x≤2) 等于 ( )
(A) 0.477 (B) 0.628 (C) 0.954 (D) 0.977
x
y
O
2
-2
分析:
由 N(0, s2) 知
x=m=0 是对称轴 (如图).
∵ P(x>2)=0.023,
∴ P(x<-2)=0.023.
则 P(-2≤x≤2)=1-2 0.023
=0.954.
C
数学建构
特别地
P(m-s
m
m-s
m+s
m
m-2s
m+2s
m
m-3s
m+3s
数学应用
例3. 某地区数学考试的成绩 X 服从正态分布, 其密度曲线如图所示, 成绩 X 位于区间 (52, 68] 的概率是多少
O
x
y
60
20
40
80
100
解:
由图知
m=60, s=8,
52=m-s, 68=m+s,
∴P(52
数学建构
数学应用
例4. 若 X~N(5, 1), 求 P(6
由 X~N(5, 1) 知 m=5, s =1.
∴P(5-1
P(5-2
=0.1359.
课堂小结
x (-∞, +∞).
正态分布密度曲线
通过频率分布直方图
x
y
O
x
y
O
x
y
a
b
正态分布
课堂小结
课堂达标
1. 若 X~N(m, s2), 则 X 位于区域 (m, m+s] 内的概率是多少
解:
若 X~N(m, s2), 则
P(m-s
所以 P(m
(1) 证明 f(x) 是偶函数;
(2) 求 f(x) 的最大值;
(3) 利用指数函数的性质说明 f(x) 的增减性.
(1)
证明:
=f(x),
∴f(x)是偶函数.
且定义域关于 x=0 对称,
(2)
解:
由解析式知 m=0,s =1,
∴ f(x) 的最大值是 f(0)
(3) f(x) 在 (-∞, 0] 上是增函数, 在 [0, +∞) 上是减函数.
