苏教版(2019)高中数学选择性必修第二册课件 9.1.1变量的相关性 课件(共16张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第二册课件 9.1.1变量的相关性 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 861.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 19:17:58 | ||
图片预览






文档简介
(共16张PPT)
9.1.1变量的相关性
学习目标
1.能通过收集现实问题中两个有关联的变量的数据作出散点图,并利用散点图直观认识变量间的相关关系;
2.线性相关的强弱数量化;
3.通过对典型案例了解线性回归分析的基本思想和方法;
情景创设
问题 1. (1) 两个变量 x, y 满足 y = 2x, x、y 之间是否相互影响, 它们存在一个什么样的关系
(2) 数学成绩的好坏与物理成绩的好坏是否相互有影响, 它们之间存在一个什么样的关系
(1) 和 (2) 的两个问题有什么相同和不同
(1) x 一变化, y 就随之而变化, 且是随 x 的 2 倍变化.同样, y 一变化, x 也就随着
变化, 且值确定.
(2)数学成绩不好, 物理成绩就可能好不起来;
数学成绩好, 物理成绩就可能会好.
数学成绩的好坏对物理成绩有影响. 但影响有多大?
这不像问题(1)那么确定, 还与其他因素有关, 对有些人影响较大, 而对另一些
人可能影响不十分大.
数学建构
这两个关系又有它的不同.
(1) 中的两个变量的关系非常确定, 而(2)中的两个变量间的关系不确定, 存在不同的情况, 即不确定因素.
(1) 中的两个变量互相影响, 一个变量的变化会引起另一个变量确定性的变化.
(2) 中也有这样的一个关系, 两个变量之间相互存在着一定的影响作用.
问题 1. (1) 两个变量 x, y 满足 y = 2x, x、y 之间是否相互影响, 它们存在一个什么样的关系
(2) 数学成绩的好坏与物理成绩的好坏是否相互有影响, 它们之间存在一个什么样的关系
(1) 和 (2) 的两个问题有什么相同和不同
数学建构
两个变量相互间有一定影响, 我们就说这两个变量之间存在着一定的相关关系.
两个变量之间, 除了像函数这样有确定的关系外,在现实生活中, 存在着许多不确定的相关关系的问题.你能举一些例子吗
(1) 商品销售收入与广告支出经费之间的关系.
(2) 粮食产量与施肥量的关系.
(3) 开发一项产品的投入与产出的关系.
(4) 个人的教育投资与收入的关系.
要分析这些关系的大小、强弱, 一是凭经验粗略估计; 二是发挥统计知识的作用, 用一些有说服力的数据来确定变量之间的相关关系.
如:
(5)人体内的脂肪含量与年龄之间的关系.
数学探究
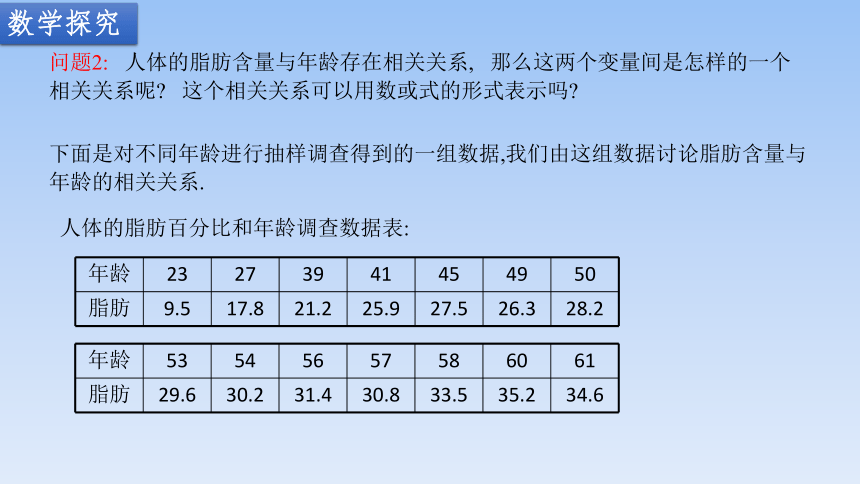
问题2: 人体的脂肪含量与年龄存在相关关系, 那么这两个变量间是怎样的一个相关关系呢 这个相关关系可以用数或式的形式表示吗
下面是对不同年龄进行抽样调查得到的一组数据,我们由这组数据讨论脂肪含量与年龄的相关关系.
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
人体的脂肪百分比和年龄调查数据表:
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
数学探究
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
借助坐标系, 作出这些数据的散点图:
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
此散点图有两特点:
(2) 从左到右在升高, 左低右高.
(1) 在某一条直线附近.
线性相关
正相关
负相关:如果散点图是从左到右下降, 即左高右低, 则称为两变量成.
数学应用
正相关
(2)吸烟有害健康
负相关
(3)高原含氧量与海拔高度
负相关
(4)学习的努力程度与学习成绩
正相关
练1:判断下列各题属于哪种相关关系?
(1)某工厂一月份总成本与该月总产量
数学应用
数学建构
散点图说明
3)如果所有的样本点都落在某一直线附近,变量之间就有线性相关关系.
1)如果所有的样本点都落在某一函数曲线上,就用该函数来描述变量之间的关系,即变量之间具有函数关系.
2)如果所有的样本点都落在某一函数曲线附近,变量之间就有相关关系.
散点图:用来判断两个变量是否具有相关关系.
数学探究
问题3. 两个变量线性相关性的强弱由什么可以看出 强弱程度由什么数据能刻划出来
数学探究
数学探究
x
0
y
数学探究
x
0
y
数学探究
x
0
y
数学探究
x
0
y
数学建构
在统计中, 常用相关系数 r 来衡量两个变量之间线性相关的强弱, r 的公式为
当 r >0时, 表明变量 x 和 y 正相关; 当 r <0时, 表明两变量之间负相关.
当|r|>0.5 时, 认为相关很强; |r|<0.30时, 认为几乎没有相关性;
当|r|越接近于1, 相关性越强; 越接近于 0, 相关性越弱.
9.1.1变量的相关性
学习目标
1.能通过收集现实问题中两个有关联的变量的数据作出散点图,并利用散点图直观认识变量间的相关关系;
2.线性相关的强弱数量化;
3.通过对典型案例了解线性回归分析的基本思想和方法;
情景创设
问题 1. (1) 两个变量 x, y 满足 y = 2x, x、y 之间是否相互影响, 它们存在一个什么样的关系
(2) 数学成绩的好坏与物理成绩的好坏是否相互有影响, 它们之间存在一个什么样的关系
(1) 和 (2) 的两个问题有什么相同和不同
(1) x 一变化, y 就随之而变化, 且是随 x 的 2 倍变化.同样, y 一变化, x 也就随着
变化, 且值确定.
(2)数学成绩不好, 物理成绩就可能好不起来;
数学成绩好, 物理成绩就可能会好.
数学成绩的好坏对物理成绩有影响. 但影响有多大?
这不像问题(1)那么确定, 还与其他因素有关, 对有些人影响较大, 而对另一些
人可能影响不十分大.
数学建构
这两个关系又有它的不同.
(1) 中的两个变量的关系非常确定, 而(2)中的两个变量间的关系不确定, 存在不同的情况, 即不确定因素.
(1) 中的两个变量互相影响, 一个变量的变化会引起另一个变量确定性的变化.
(2) 中也有这样的一个关系, 两个变量之间相互存在着一定的影响作用.
问题 1. (1) 两个变量 x, y 满足 y = 2x, x、y 之间是否相互影响, 它们存在一个什么样的关系
(2) 数学成绩的好坏与物理成绩的好坏是否相互有影响, 它们之间存在一个什么样的关系
(1) 和 (2) 的两个问题有什么相同和不同
数学建构
两个变量相互间有一定影响, 我们就说这两个变量之间存在着一定的相关关系.
两个变量之间, 除了像函数这样有确定的关系外,在现实生活中, 存在着许多不确定的相关关系的问题.你能举一些例子吗
(1) 商品销售收入与广告支出经费之间的关系.
(2) 粮食产量与施肥量的关系.
(3) 开发一项产品的投入与产出的关系.
(4) 个人的教育投资与收入的关系.
要分析这些关系的大小、强弱, 一是凭经验粗略估计; 二是发挥统计知识的作用, 用一些有说服力的数据来确定变量之间的相关关系.
如:
(5)人体内的脂肪含量与年龄之间的关系.
数学探究
问题2: 人体的脂肪含量与年龄存在相关关系, 那么这两个变量间是怎样的一个相关关系呢 这个相关关系可以用数或式的形式表示吗
下面是对不同年龄进行抽样调查得到的一组数据,我们由这组数据讨论脂肪含量与年龄的相关关系.
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
人体的脂肪百分比和年龄调查数据表:
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
数学探究
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
借助坐标系, 作出这些数据的散点图:
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
此散点图有两特点:
(2) 从左到右在升高, 左低右高.
(1) 在某一条直线附近.
线性相关
正相关
负相关:如果散点图是从左到右下降, 即左高右低, 则称为两变量成.
数学应用
正相关
(2)吸烟有害健康
负相关
(3)高原含氧量与海拔高度
负相关
(4)学习的努力程度与学习成绩
正相关
练1:判断下列各题属于哪种相关关系?
(1)某工厂一月份总成本与该月总产量
数学应用
数学建构
散点图说明
3)如果所有的样本点都落在某一直线附近,变量之间就有线性相关关系.
1)如果所有的样本点都落在某一函数曲线上,就用该函数来描述变量之间的关系,即变量之间具有函数关系.
2)如果所有的样本点都落在某一函数曲线附近,变量之间就有相关关系.
散点图:用来判断两个变量是否具有相关关系.
数学探究
问题3. 两个变量线性相关性的强弱由什么可以看出 强弱程度由什么数据能刻划出来
数学探究
数学探究
x
0
y
数学探究
x
0
y
数学探究
x
0
y
数学探究
x
0
y
数学建构
在统计中, 常用相关系数 r 来衡量两个变量之间线性相关的强弱, r 的公式为
当 r >0时, 表明变量 x 和 y 正相关; 当 r <0时, 表明两变量之间负相关.
当|r|>0.5 时, 认为相关很强; |r|<0.30时, 认为几乎没有相关性;
当|r|越接近于1, 相关性越强; 越接近于 0, 相关性越弱.
