苏教版(2019)高中数学选择性必修第二册课件 9.1.2线性回归方程 课件(共21张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学选择性必修第二册课件 9.1.2线性回归方程 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1004.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-25 19:18:23 | ||
图片预览



文档简介
(共21张PPT)
9.1.2线性回归方程
学习目标
1.通过对典型案例的探究线性回归方程;
2.会用线性回归方程进行实际预测;
3.进一步了解线性回归分析的基本思想和方法.
情景创设
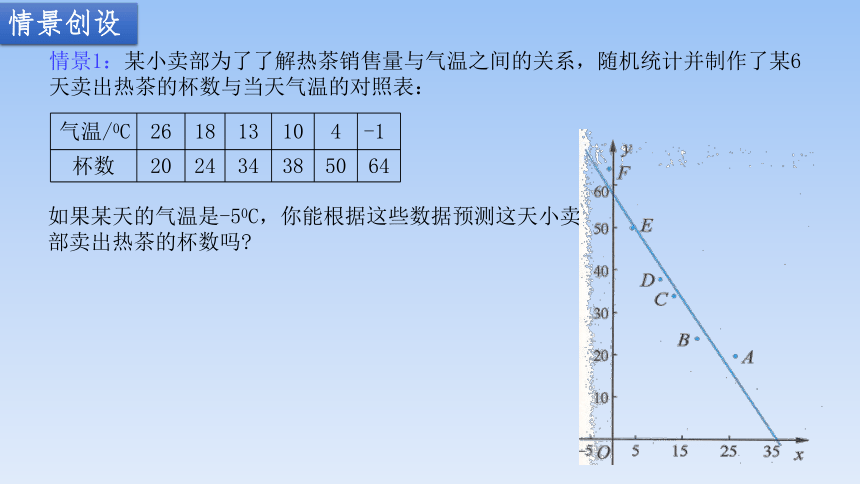
情景1:某小卖部为了了解热茶销售量与气温之间的关系,随机统计并制作了某6天卖出热茶的杯数与当天气温的对照表:
气温/0C 26 18 13 10 4 -1
杯数 20 24 34 38 50 64
如果某天的气温是-50C,你能根据这些数据预测这天小卖部卖出热茶的杯数吗
情景创设
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
你能预测37岁时的脂肪含量吗
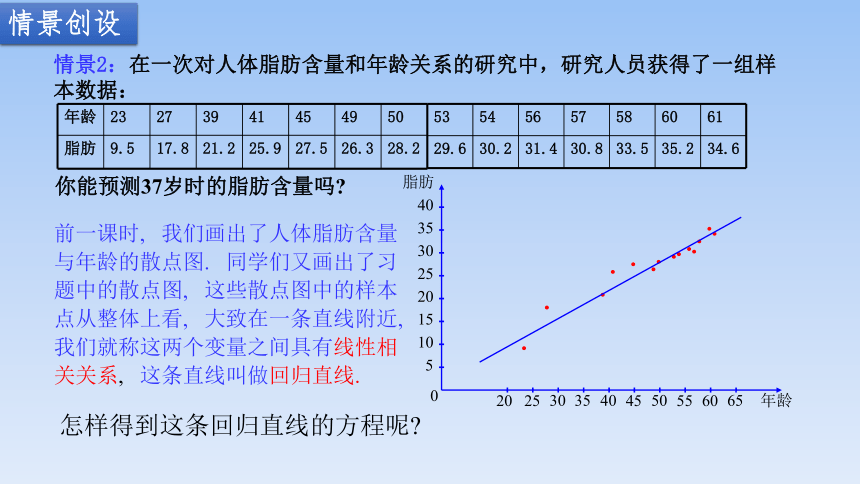
情景2:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
53 54 56 57 58 60 61
29.6 30.2 31.4 30.8 33.5 35.2 34.6
前一课时, 我们画出了人体脂肪含量与年龄的散点图. 同学们又画出了习题中的散点图, 这些散点图中的样本点从整体上看, 大致在一条直线附近, 我们就称这两个变量之间具有线性相关关系, 这条直线叫做回归直线.
怎样得到这条回归直线的方程呢
数学探究
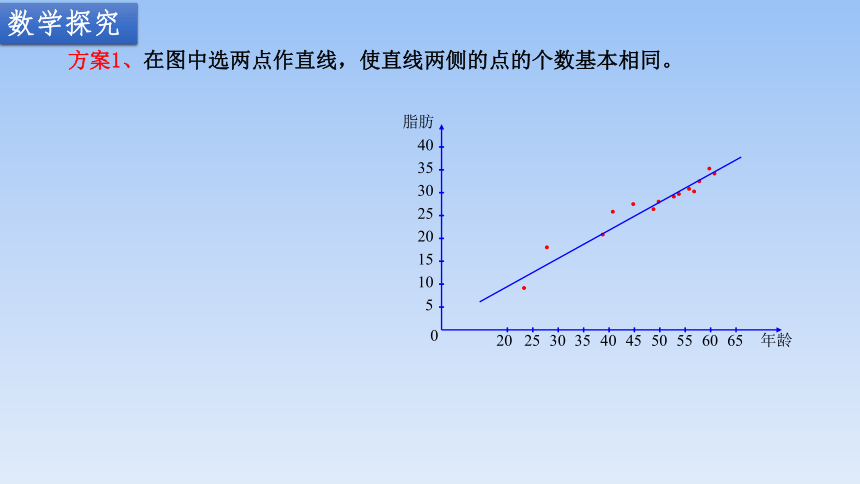
方案1、在图中选两点作直线,使直线两侧的点的个数基本相同。
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
数学探究
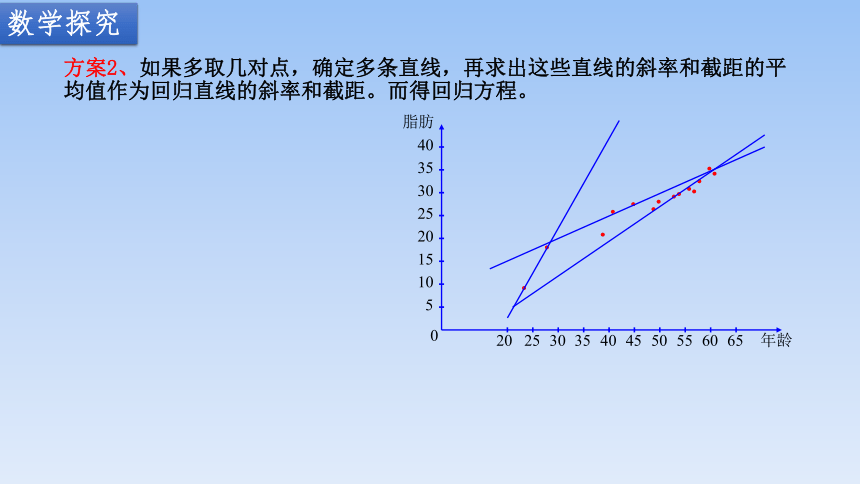
方案2、如果多取几对点,确定多条直线,再求出这些直线的斜率和截距的平均值作为回归直线的斜率和截距。而得回归方程。
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
数学探究
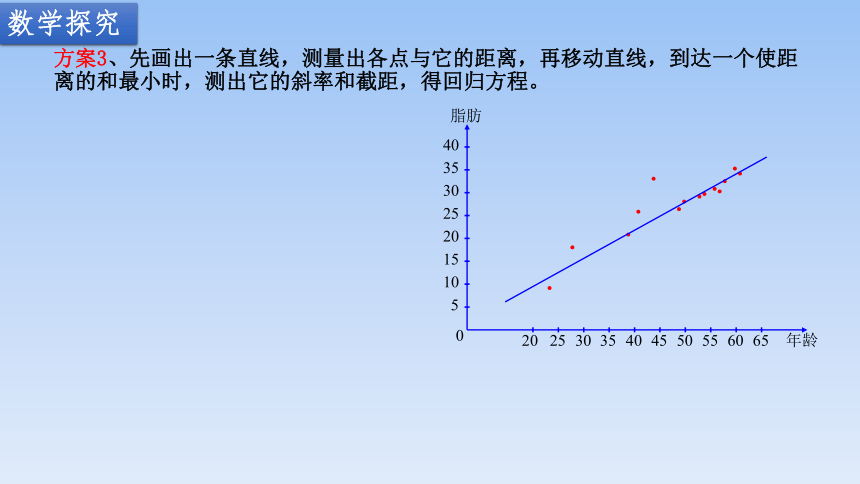
方案3、先画出一条直线,测量出各点与它的距离,再移动直线,到达一个使距离的和最小时,测出它的斜率和截距,得回归方程。
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
数学探究
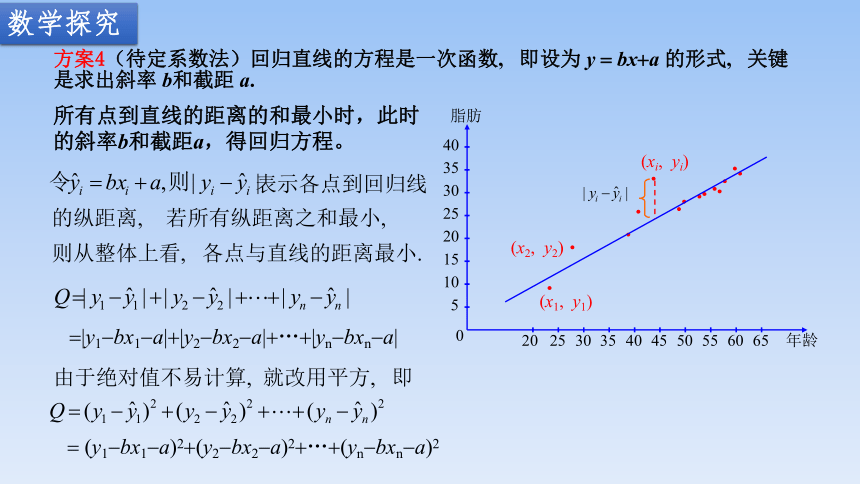
方案4(待定系数法)回归直线的方程是一次函数, 即设为 y = bx+a 的形式, 关键是求出斜率 b和截距 a.
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
(x1, y1)
(x2, y2)
(xi, yi)
所有点到直线的距离的和最小时,此时的斜率b和截距a,得回归方程。
表示各点到回归线
若所有纵距离之和最小,
则从整体上看, 各点与直线的距离最小.
的纵距离,
=|y1-bx1-a|+|y2-bx2-a|+…+|yn-bxn-a|
由于绝对值不易计算, 就改用平方, 即
= (y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2
数学建构
经过推导可得:
即要使 Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2最小, a, b 应取什么值
求出 a, b 的值, 就得到回归方程
这种使样本数据各点到回归直线的距离的平方和最小来得到回归直线的方法叫做最小二乘法.
数学应用
如某人37岁, 将 x = 37 代入回归方程
≈20.90,
得
即这个人的体内脂肪含量约为20.90%左右.
你能预测37岁时的脂肪含量吗
例1:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
53 54 56 57 58 60 61
29.6 30.2 31.4 30.8 33.5 35.2 34.6
数学应用
练、为了对公式的理解, 我们求下面两个变量的线性回归方程, 并估计当数学为98分成绩时, 物理可能是多少分的成绩.
数学 87 95 62 78 70 65
物理 82 89 64 75 68 66
斜率
≈0.56,
截距
=74-0.56 74.5
=32.28.
∴回归方程为:
解:
当 x=98 时,
≈87
当数学为98分成绩时, 估计物理可能是87分的成绩.
数学应用
数学应用
课堂小结
1、求回归直线方程的步骤
第一步:列表;
第四步:写出回归直线方程.
2、回归方程的应用
预测
课堂达标
1.三点(3,10),(7,20),(11,24)的线性回归方程是 ( )
D
课堂达标
2.以下四个散点图中,两个变量的关系适合用线性回归模型刻画的是( )
A.①② B.①③ C.②③ D.③④
答案:B
课堂达标
3.(多选)有关线性回归的说法,正确的是( )
A.相关关系的两个变量不是因果关系
B.散点图能直接反映数据的相关程度
C.回归直线最能代表线性相关的两个变量之间的关系
D.任意一组数据都有回归方程
答案:ABC
课堂达标
C.若该大学某女生身高增加1 cm,则其体重约增加0.85 kg
D.若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg
答案:D
课堂达标
5.对具有线性相关关系的变量x和Y,测得一组数据如下表:
若已求得它们的回归直线方程的斜率为6.5,则这条回归直线方程为 .
x 2 4 5 6 8
Y 30 40 60 50 70
课后探究
第x天 1 4 9 16 25 36 49
高度y/cm 0 4 7 7 11 12 13
课后探究
课后探究
非线性回归模型的分析步骤:
1.绘制散点图
2.观察散点图,选取适合的函数模型,通过换元法转化成线性回归模型并转化数据
3.求换元后的回归直线方程
4.建立非线性回归模型
9.1.2线性回归方程
学习目标
1.通过对典型案例的探究线性回归方程;
2.会用线性回归方程进行实际预测;
3.进一步了解线性回归分析的基本思想和方法.
情景创设
情景1:某小卖部为了了解热茶销售量与气温之间的关系,随机统计并制作了某6天卖出热茶的杯数与当天气温的对照表:
气温/0C 26 18 13 10 4 -1
杯数 20 24 34 38 50 64
如果某天的气温是-50C,你能根据这些数据预测这天小卖部卖出热茶的杯数吗
情景创设
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
你能预测37岁时的脂肪含量吗
情景2:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
53 54 56 57 58 60 61
29.6 30.2 31.4 30.8 33.5 35.2 34.6
前一课时, 我们画出了人体脂肪含量与年龄的散点图. 同学们又画出了习题中的散点图, 这些散点图中的样本点从整体上看, 大致在一条直线附近, 我们就称这两个变量之间具有线性相关关系, 这条直线叫做回归直线.
怎样得到这条回归直线的方程呢
数学探究
方案1、在图中选两点作直线,使直线两侧的点的个数基本相同。
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
数学探究
方案2、如果多取几对点,确定多条直线,再求出这些直线的斜率和截距的平均值作为回归直线的斜率和截距。而得回归方程。
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
数学探究
方案3、先画出一条直线,测量出各点与它的距离,再移动直线,到达一个使距离的和最小时,测出它的斜率和截距,得回归方程。
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
数学探究
方案4(待定系数法)回归直线的方程是一次函数, 即设为 y = bx+a 的形式, 关键是求出斜率 b和截距 a.
年龄
脂肪
0
20
25
30
35
40
45
50
55
60
65
5
10
15
20
25
30
35
40
(x1, y1)
(x2, y2)
(xi, yi)
所有点到直线的距离的和最小时,此时的斜率b和截距a,得回归方程。
表示各点到回归线
若所有纵距离之和最小,
则从整体上看, 各点与直线的距离最小.
的纵距离,
=|y1-bx1-a|+|y2-bx2-a|+…+|yn-bxn-a|
由于绝对值不易计算, 就改用平方, 即
= (y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2
数学建构
经过推导可得:
即要使 Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2最小, a, b 应取什么值
求出 a, b 的值, 就得到回归方程
这种使样本数据各点到回归直线的距离的平方和最小来得到回归直线的方法叫做最小二乘法.
数学应用
如某人37岁, 将 x = 37 代入回归方程
≈20.90,
得
即这个人的体内脂肪含量约为20.90%左右.
你能预测37岁时的脂肪含量吗
例1:在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
53 54 56 57 58 60 61
29.6 30.2 31.4 30.8 33.5 35.2 34.6
数学应用
练、为了对公式的理解, 我们求下面两个变量的线性回归方程, 并估计当数学为98分成绩时, 物理可能是多少分的成绩.
数学 87 95 62 78 70 65
物理 82 89 64 75 68 66
斜率
≈0.56,
截距
=74-0.56 74.5
=32.28.
∴回归方程为:
解:
当 x=98 时,
≈87
当数学为98分成绩时, 估计物理可能是87分的成绩.
数学应用
数学应用
课堂小结
1、求回归直线方程的步骤
第一步:列表;
第四步:写出回归直线方程.
2、回归方程的应用
预测
课堂达标
1.三点(3,10),(7,20),(11,24)的线性回归方程是 ( )
D
课堂达标
2.以下四个散点图中,两个变量的关系适合用线性回归模型刻画的是( )
A.①② B.①③ C.②③ D.③④
答案:B
课堂达标
3.(多选)有关线性回归的说法,正确的是( )
A.相关关系的两个变量不是因果关系
B.散点图能直接反映数据的相关程度
C.回归直线最能代表线性相关的两个变量之间的关系
D.任意一组数据都有回归方程
答案:ABC
课堂达标
C.若该大学某女生身高增加1 cm,则其体重约增加0.85 kg
D.若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg
答案:D
课堂达标
5.对具有线性相关关系的变量x和Y,测得一组数据如下表:
若已求得它们的回归直线方程的斜率为6.5,则这条回归直线方程为 .
x 2 4 5 6 8
Y 30 40 60 50 70
课后探究
第x天 1 4 9 16 25 36 49
高度y/cm 0 4 7 7 11 12 13
课后探究
课后探究
非线性回归模型的分析步骤:
1.绘制散点图
2.观察散点图,选取适合的函数模型,通过换元法转化成线性回归模型并转化数据
3.求换元后的回归直线方程
4.建立非线性回归模型
